数学コラムの目次
京の算数学問題#561

アイデア数理塾はこちら
京の算数学コラム
みなさんこんにちは!京都市中京区で学習塾を運営しております。油谷拓哉(ゆたに たくや)です!
小学4年生での算数のつまづきの多くは小数ではないでしょうか?
ちょうど3年生から新しい概念が広がり今まで1→10000と位が増えていく一方だったのが小数が入ると0→0.001などと途端に0~1のあいだの数を考える必要が出てきます。
そこでつまづきの多くが小数のたし算ひき算とかけ算の筆算の違いです。
今日はそんなお話。
数字の桁を理解しよう!
私たちが馴染みのあるケタとは、
例えば、12345→一万二千三百四十五というように一の位から始まりどんどん大きくなっていくものですよね。
ただ、小数の場合は一の位から徐々に小さくなっていき限りなく0に近づいていきます。
例えば、1.2345の場合ですが、
1を一の位とし、2が小数第一位(10分の1の位)、3が小数第二位(100分の1の位)というようになります。
これを意識して次の問題へ行きましょう。
【ケタをそろえる!】小数のたし算ひき算の筆算
例えば29+30の場合。
このような筆算になります。
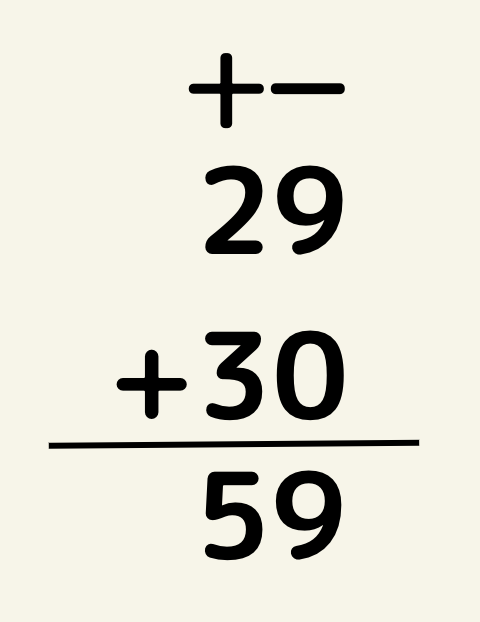
一見右詰めで計算しているように思いますが、それぞれケタがそろっています。
次に小数の場合です。
小数の筆算は同様にケタを合わせます。

わかりにくければ小数点の位置を縦にそろえましょう!
では、問題です2.9+3の計算を筆算でしたい。
次の画像の間違いを指摘してください。
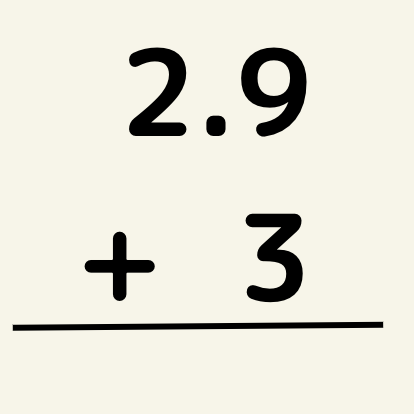
間違いはここです!
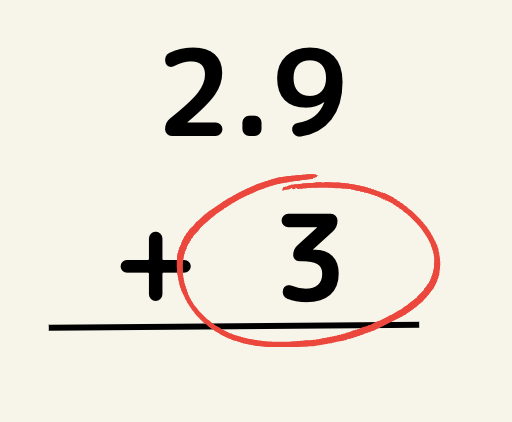
3は一の位ですので、小数にそろえるなら3.0となります。
ですので正しい式は
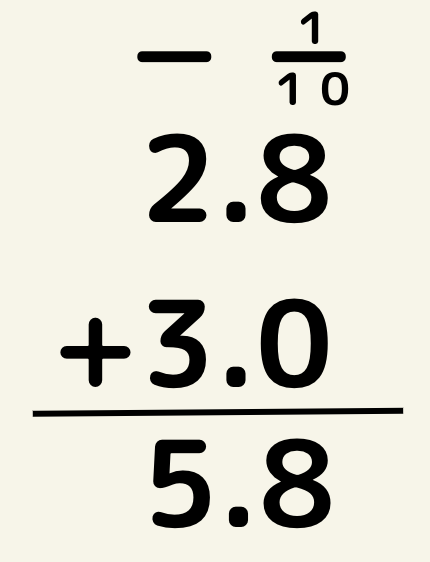
こうなります。
ひき算も同様ですので、たし算ひき算の式は小数点をそろえるということを覚えておきましょう!
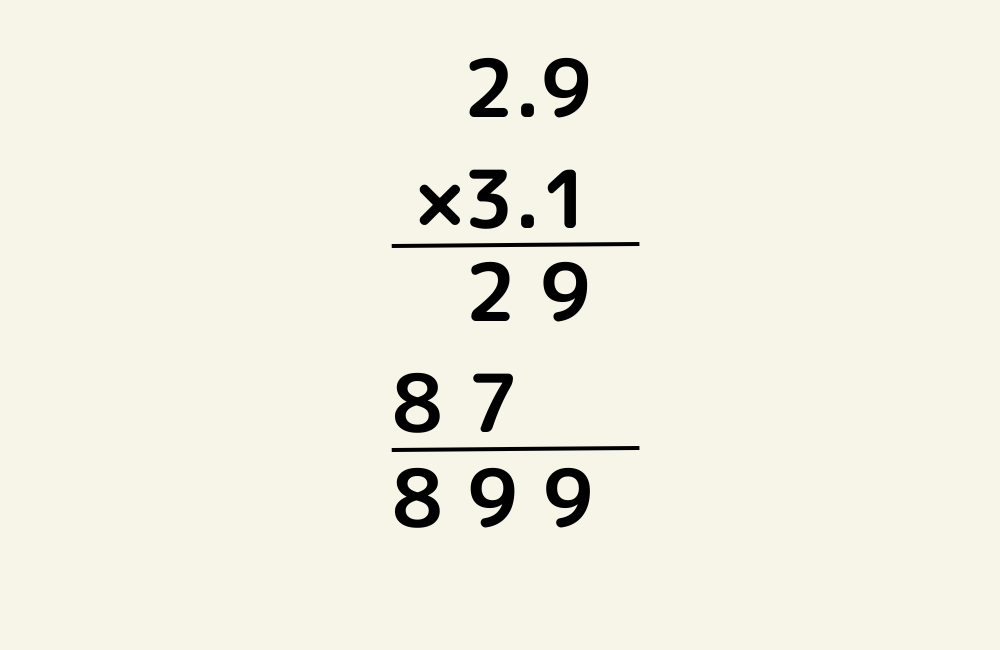
【そろえなくてもいい!】小数のかけ算の筆算
一方でかけ算の場合はそろえなくても良いです。
例えば
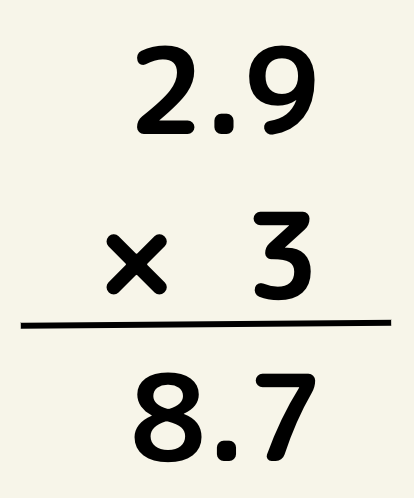
このように計算ができてしまいます。
なぜかけ算はそろえなくてもいいの?
例えばこの場合、
2.9×3という式を考えていきましょう。
2.9は0.1が29こ集まった数ですので、
29×0.1と表すことができます。
つまり、2.9×3=29×0.1×3=29×3×0.1となります。
(かけ算は順番を入れ替えても大丈夫)
言い換えれば29×3をしてから0.1をかければいいので、
かけ算の筆算の手順もまず29×3をしてから小数点の位置を1個左側にずらしたはずです。
この操作自体が29×3の答えに0.1をかけていることと同義になります。
それでも納得しないときは、、、
子どもたちのつまづきは「ケタをなんでそろえないといけないの??」です。
ただ、この課題は早々に解決できる問題ではありません。
というよりも算数のなぜ?は数学を学んでから解決できるものが多いからです。
どうしても納得しない場合はこのやり方を試してみてください!

ちょっと回りくどいやり方ではありますが、そもそもつまづいているポイントは小数点の位置を最後にずらすことでは無くケタをそろえることです。
ですので無理やりケタをそろえてしまってから計算すると問題は解決するわけです。
慣れてきたら自分でできるようになるので、もしケタを揃えることで納得がいかなければぜひお試しください!
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#561