数学コラムの目次
今日の数学問題#208

今日の数学ブログ
恒等式という言葉を初めて知るのは高校生でしょう。
恒等式を解け!という問題に少々違和感を感じることもあると思います。
「方程式とどう違うの?」今日はそんなお悩みにお答えしていきたいと思います!
恒等式ってなに?
恒等式とは、どんな数を代入しても成立する式です。
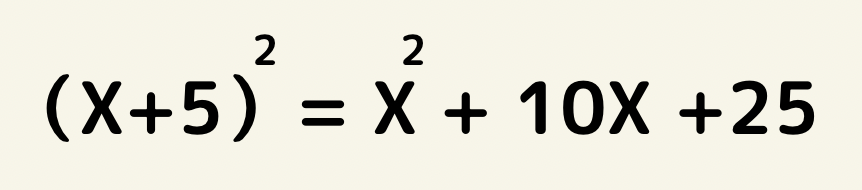
この式のxに1を代入しても5を代入しても左辺=右辺になります。
こういった式を恒等式と言います。
方程式とどう違うの?
方程式はxが特定の値の時だけ成り立つ式のことです。
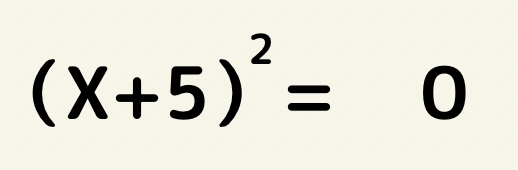
例えばこの場合、x=-5でしかこの式は成り立ちません。
これが方程式と恒等式の違いになります。
恒等式の解き方
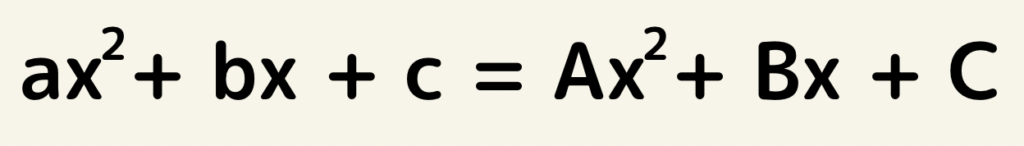
が変数xについての恒等式であるとき、
A=a,B=b,C=cが成り立つ。
つまり、左辺と右辺の係数が等しい。
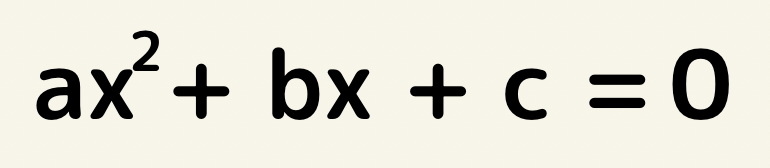
これがxについての恒等式の場合。
a=0,b=0,c=0となる。
係数比較法
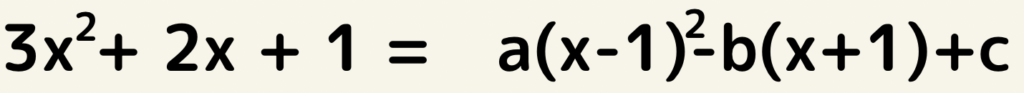
係数比較法は上記の法則を利用する解法です。
この方法が1番使うかなと思いますので是非マスターしましょう!
右辺を展開して整理すると
ax^2+(-2a-b)x+a-b+c
となる。
ここで3つの方程式を立てることができる。
3=a
2=-2a-b
1=a-b+c
この連立方程式を解くと、a=3,b=-8,c=-10となる。
数値代入法

この方法はxに適当な数字を入れて簡単にしていきます。
x=0の時、1=2a+b-2c
x=1の時、7=-c,c=-7
x=2の時、17=-b,b=-17
よって、a=2,b=-17,c=-7となる。
これを右辺に当てはめ整理すると、
2x^2+4x+1となりこれは左辺と等しくなる。
よって確かに与式は恒等式になっている。
このように適当に代入しa,b,cを求めた時点では必要条件を示しただけで全てのxについて成り立つ証明ができていません。
そのため、a,b,cを代入し十分条件を証明する必要があります。
係数比較法であればこの証明は不要なので基本的には係数比較法で問題ないでしょう。
計算がややこしくなる場合のみ数値代入法を使用した方が、計算が楽になる場合がありますので偏差値60あたりを目指す生徒は是非とも覚えておきましょう。
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
今日の数学 解答#208



