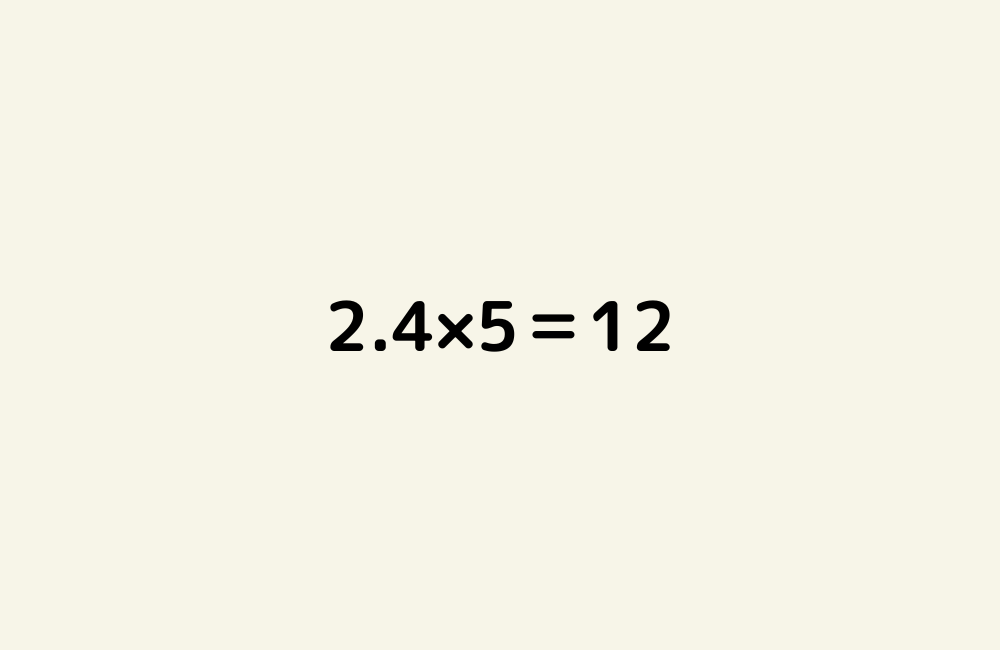数学コラムの目次
京の算数学問題#1007

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で学習塾を運営しております、油谷拓哉(ゆたに たくや)です。
小学4年生になると、「算数の壁」と呼ばれるほど学習内容が一気に難しくなります。
3年生までは「計算のルールを覚える」ことが中心でしたが、4年生からは「なぜその計算をするのか?」といった考える力が求められます。
例えば、
- 帯分数と仮分数 ーー 分数の概念を深く理解する必要がある
- 小数のかけ算・わり算 ーー 小数の桁の考え方が難しくなる
- 分度器の使い方 ーー 角度の概念と作図の正確さが求められる
このように、数字の操作だけでなく、数の意味や関係性を考えながら解く力が必要になり、つまずきやすいポイントが増えていきます。
「学校の授業は理解できているのに、応用問題になると正解できない」
「計算はできるのに、文章問題になると混乱する」
このような悩みを持つお子さんも多いのではないでしょうか?
そこで今回は、小学4年生が特につまずきやすい単元について、ポイントと対策を詳しく解説していきます!
1. 帯分数と仮分数
つまずきポイント
- 帯分数と仮分数を変換する意味がわからない
- 仮分数の計算ができても、帯分数の概念があいまい
- 分数の大小関係がつかめない
指導の流れ
(1) 実物を使って分数のイメージをつかむ
- ピザやチョコを分ける
- 1枚のピザを「1」として、2/3や1と1/2を実際に表現させる
- 数直線を活用する
- 0〜2の数直線を描き、「1と3/4」「7/4」を対応させる
(2) 帯分数と仮分数の変換を手順化
- 「1と3/4」を仮分数にする手順
- 1を「4/4」にする
- 4/4 + 3/4 = 7/4
- 逆の変換も練習
- 9/4 → 4/4 + 4/4 + 1/4 = 2と1/4
(3) 分数の大小を比べる練習
- 分母が同じときは分子が大きいほうが大きい(例:3/7と5/7)
- 分母が違うときは通分する習慣をつける
2. 小数のかけ算・わり算
つまずきポイント
- 整数のかけ算・わり算と混同してしまう
- 小数点の位置を間違える
- 小数の感覚がつかめず、答えの見当がつかない
指導の流れ
(1) 「小数の概念」をしっかり理解する
- 0.1や0.01を数直線で示し、1との関係を明確にする
- 0と1の間に桁が存在するイメージを作る
→小数第一位や小数第二位など桁の呼び方を覚えておくと良い
(2) 小数のかけ算は「整数として計算 → 小数点を調整」
- 例:「1.2 × 3」
- まず「12 × 3 = 36」と考える
- 小数点を元の位置に戻す(答えは3.6)
- 整数と小数の計算を同じ感覚でやらせない
(3) 小数のわり算は「わり算の意味を確認」
- 「12 ÷ 4 = 3」なら「1.2 ÷ 4 = 0.3」となる感覚を養う
- 小数点の移動ルールを整理する(整数に直して計算する方法も使う)
3. 分度器の使い方(角度の学習)
つまずきポイント
- 分度器のどこを0°に合わせるかわからない
- 内側の目盛りと外側の目盛りを間違える
- 角度の大きさの感覚がつかめていない
指導の流れ
(1) 分度器の基本的な使い方を確認する
- 「中心」をしっかり合わせる練習を何度も行う
- 内側の目盛りと外側の目盛りの違いを強調(角が右向きなら外側、左向きなら内側)
(2) 角度の感覚を養う
- 90°は直角、180°は一直線の角として意識させる
- 「45°は90°の半分」「120°は90°より少し大きい」など、感覚で予測する練習をする
4. がい数と四捨五入
つまずきポイント
- 「がい数」と「四捨五入」の違いを理解していない
- 10の位や100の位での四捨五入を間違える
- 「おおよその数」の意味が曖昧
指導の流れ
(1) 四捨五入のルールを整理する
- 四捨五入の基本ルール(5以上切り上げ、4以下切り捨て)を明確にする
- どの位を四捨五入するかを色分けする(例:1234 → 1000の位までなら「1000」)
- 〇〇までの概数でと上から〇桁をの区別を作る
(2) がい数のイメージをつかむ
- 「1234を1000の位までのがい数にすると?」→「だいたい1000」
- 「約いくら?」という実生活の問題で考えさせる
5. 計算の工夫(四則混合)
つまずきポイント
- 「かけ算を先にする」ルールを覚えていない
- 数を分ける計算方法に戸惑う
- 暗算で処理しようとしてミスが増える
指導の流れ
(1) 計算の順序をルール化する
- 「足し算と掛け算が混ざった式はどちらを先に計算する?」→「掛け算!」
- 実際の例で比較
- (2 + 3) × 4 = 5 × 4 = 20
- 2 + (3 × 4) = 2 + 12 = 14
(2) 分けて計算する方法を習得する
- 例:「25 + 17」→ 25 + 5 + 12 = 30 + 12 = 42
- 「なぜこうするのか?」を質問して、考えさせる
6. 立体の展開図
つまずきポイント
- 展開図が立体になるイメージができない
- どの面がどこにつながるかわからない
指導の流れ
(1) 実際に作ってみる
- 紙を切って立方体や直方体の展開図を作らせる
- 展開図を見せて「組み立てたらどうなるか?」を考えさせる
(2) 展開図の種類を整理する
- 同じ立方体でも展開図はいくつもあると伝える
- 「この展開図はどんな立体になる?」クイズ形式で出題
まとめ:4年生の算数の指導のポイント
具体例を使って「なぜ?」を考えさせる
視覚的・体験的に理解させる(図や実物を活用)
言葉の意味をしっかり整理する(がい数・分数・展開図など)
答えの予測を習慣づけ、計算ミスを減らす
4年生の算数は、「作業」から「思考」へとシフトする時期です。
理由を考えながら学習することで、算数を得意にしていきましょう!
京の算数学 解答#1007