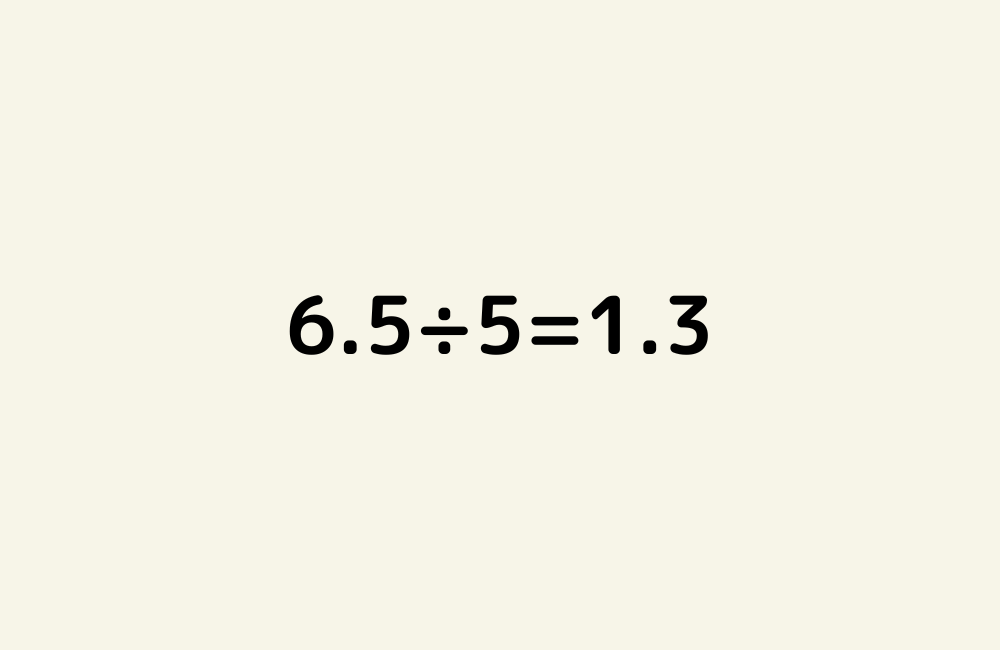数学コラムの目次
京の算数学問題#974

アイデア数理塾はこちら
算数学コラム
こんにちは!京都市中京区で学習塾を運営しております、油谷拓哉(ゆたに たくや)です!
小学4年生になると、小数のわり算が登場しますが、4年生で学ぶのは「小数 ÷ 整数」です。
小数点の位置がわからなくなる…
あまりが出たらどうするの?
四捨五入ってどうやるの?
こんな悩みを抱えるお子さんも多いのではないでしょうか?
今回は、小数 ÷ 整数の基本から筆算のやり方、四捨五入のコツ、「10分の1のくらいまで」と「概数」の違いまで詳しく解説します!
1. 小数 ÷ 整数って何?
小数 ÷ 整数は、小数を整数で割る計算のことです。
例えば、こんな問題があります。
- 12.6 ÷ 3 = 4.2
- 8.4 ÷ 2 = 4.2
- 7.5 ÷ 5 = 1.5
整数のわり算とほぼ同じですが、小数点の位置に気をつける必要があります。
2. 小数 ÷ 整数の筆算のやり方!
🌟 例題1:12.6 ÷ 3
💡 ステップ解説!
- 小数点を気にせず普通の筆算を行う。
- 小数点を商(答え)の真上にそのまま書く!
📖 筆算で解いてみよう!
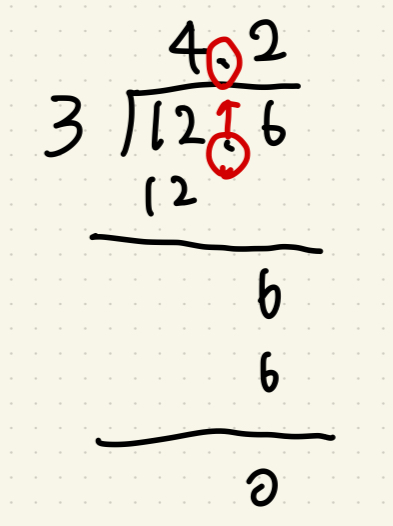
✅ 答え:4.2
👉 ポイント! 小数点は「そのまま真上に上げる」と覚えましょう!
🌟 例題2:8.4 ÷ 2
💡 ステップ解説!
- 8 ÷ 2 = 4
- 4 ÷ 2 = 2
📖 筆算の流れ!
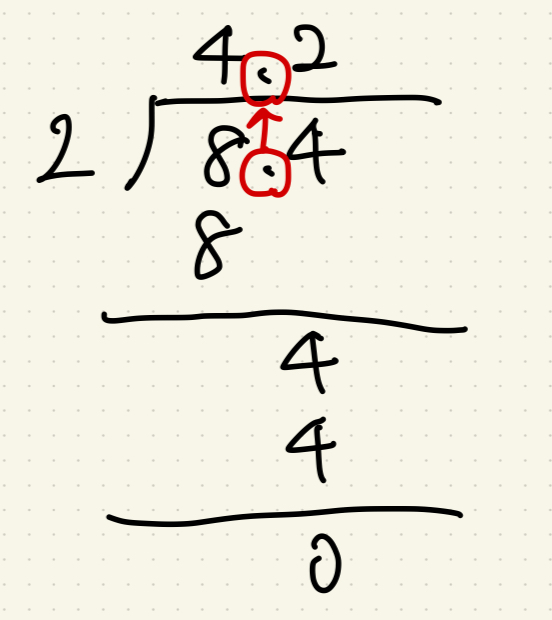
✅ 答え:4.2
👉 小数点は「そのまま上に!」を意識すればOK!
3. 小数のわり算で四捨五入が必要な場合!
四捨五入は、指定された位まででのだいたいの数を求めることです。
例えば、12.36 ÷ 5 という問題があるとします。
🌟 例題:12.36 ÷ 5 を10分の1のくらいまで求める場合!
- 普通に筆算を行う。
- 商(答え)が2.472 となる。
- 10分の1のくらい(小数第1位)は「4」の位。
- 2.472 → 2.5(7を四捨五入して繰り上げ!)
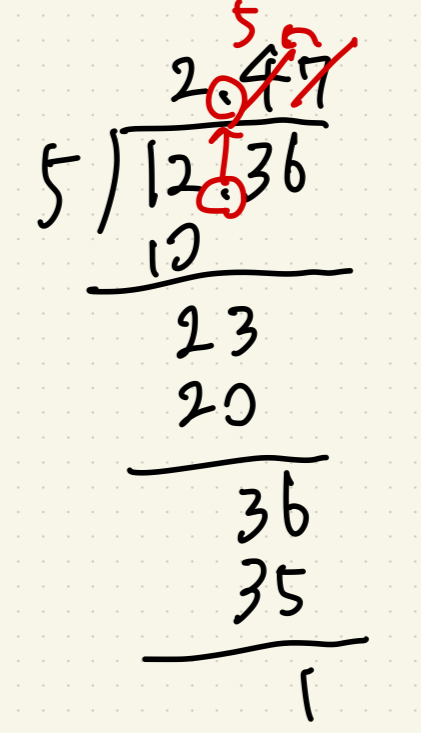
✅ 答え:2.5
4. 10分の1のくらいまで求める vs 概数で表すの違い!
小数のわり算の筆算の中でも特に難しくさせる単元が四捨五入とあまりの求め方です。
ここではあまりを求める問題と四捨五入をする問題について違いをまとめます。
① 10分の1のくらいまで求め、あまりを求めよ
10分の1のくらいまで求めあまりを求めよというのは「10分の1の値まで計算をしあまりをだしなさい」という意味です。
例えば上記の問題で言えば、
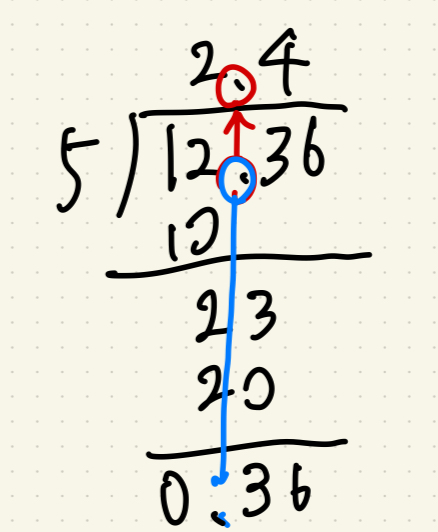
となるので、10分の1の位(小数第1位)まで値を求め、整数のわり算と同じように進めていきます。
その後小数点をそのまま商にあげ、2.4が商となる。
あまりも同様に小数点を下に置き36の前に点をつけるのであまりは0.36となる。
小数点をそのままというのは移動しているわけではなくあくまで桁を揃えるという意味になることに注意しておこう。
② 10分の1の位までのがい数で表せ
10分の1の位までのがい数で表せとは「100分の1の位の値を四捨五入し大体の商を求めよう」という意味です。
この場合、余りは問われていないので、特に求める必要はないことも覚えておこう。
- 四捨五入して小数第1位までで切り捨て・切り上げ。
- あまりは求めず、キリのいい数字にする。
5. 文章題で実践!
🌟 例題:8.5mのリボンを3人で分けると1人あたり何m?
→ 「10分の1のくらいまで求め、あまりを求める」場合
- 8.5 ÷ 3 = 2.8あまり0.1
- 小数第1位でストップ!
- 答え:2.8m あまり0.1m!
🌟 例題:7.5kgの米を4人で分けると1人あたり何kg?
→ 「10分の1の位までのがい数で表す」場合
がい数で表す場合答えに約をつけることを忘れずに!
- 7.5 ÷ 4 = 1.875
- 小数第1位で四捨五入!
- 答え:約1.9kg
6. まとめ:コツをつかめば小数のわり算も怖くない!
✨ 今日のポイント!
- 小数点は答えの真上!
- 四捨五入は位を確認!
- 「あまり」と「がい数」の違いを意識!
繰り返し練習することで、自然とコツがつかめるようになります。
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)でした!
算数好きあつまれ〜!
京の算数学 解答#974