数学コラムの目次
京の算数学問題#982

アイデア数理塾はこちら
算数学コラム
みなさん、こんにちは!
京都市中京区で学習塾を運営している 油谷拓哉(ゆたに たくや) です。
今日は 小学6年生で学ぶ「線対称・点対称」 について、基本の考え方から問題の解き方までわかりやすく解説します!
「線対称ってなに?」
「点対称の図形ってどうやって見分けるの?」
「問題になるとよくわからなくなる…」
こんな疑問をスッキリ解決するために、 考え方のコツ や 例題 を交えて説明していきます!
🔍 線対称と点対称とは?
まず、「対称」 という言葉の意味を確認しましょう!
対称とは、ある決まった方法で折り返したときや回転させたときに、元の形とピッタリ重なる性質 のことです。
対称には「線対称」 と「点対称」 の2種類があります!
線対称とは?
✅ 線対称の図形とは?
線対称の図形 とは、ある1本の線で折りたたんだときに、左右がピッタリ重なる図形 のことです。
この 折りたたむ線 のことを 対称の軸(たいしょうのじく) といいます!
✅ 線対称の例
以下の図形は 線対称 になります。
✅ 線対称の図形の例
- 正方形(対角線や辺の中心で折ると重なる)
- 長方形(縦と横の中心で折ると重なる)
- 正三角形(3本の対称の軸がある)
- 円(どの直径でも線対称)
- アルファベット「A」「M」「T」 など
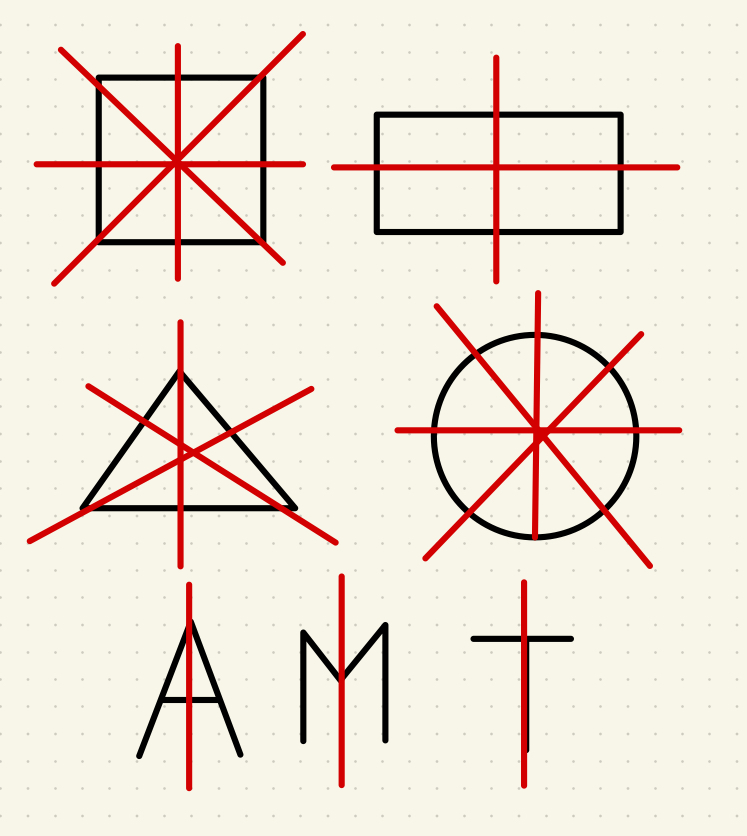
たとえば、ハートのマーク や チョウの形 も線対称ですね!
対称の軸は1本とは限らないので注意が必要です!
🎯 線対称の問題を解いてみよう!
例題①:線対称かどうかを判断しよう!
次の図形は 線対称の図形でしょうか?また、対称の軸は何本ありますか?
① 正方形
② ひし形
③ 五角形
✅ 解き方
- 正方形 → 4本の対称の軸(縦・横・対角線)
- ひし形 → 2本の対称の軸(対角線)
- 五角形 → 正五角形 なら5本の対称の軸、ふつうの五角形なら線対称ではない
✅ 答え
① 正方形 → 線対称(4本)
② ひし形 → 線対称(2本)
③ 五角形 → 正五角形なら線対称(5本)、ふつうの五角形は線対称ではない
点対称とは?
✅ 点対称の図形とは?
点対称の図形 とは、ある1つの点を中心に180°回転させると、元の形とピッタリ重なる図形 のことです。
この中心の点を 対称の中心(たいしょうのちゅうしん) といいます!
✅ 点対称の例
✅ 点対称の図形の例
- 正方形(中心を180°回転させると重なる)
- ひし形(対角線の交点を中心に180°回転させると重なる)
- アルファベット「N」「S」「Z」 など

例えば、アルファベットの 「S」や「Z」 は、180°回転させても同じ形になりますね!
🎯 点対称の問題を解いてみよう!
例題②:点対称の図形を見つけよう!
次の図形は 点対称の図形でしょうか?
① 正方形
② 正三角形
③ ひし形
✅ 解き方
- 正方形 → 点対称(中心を180°回転させると重なる)
- 正三角形 → 点対称ではない(180°回転させると形が変わる)
- ひし形 → 点対称(中心を180°回転させると重なる)
✅ 答え
① 正方形 → 点対称
② 正三角形 → 点対称ではない
③ ひし形 → 点対称
ここから正方形やひし形は線対称でもあり、点対称でもあることが分かります。
どちらかではなく両方の可能性があることも覚えておきましょう!
💡 線対称・点対称の問題を解くコツ
1️⃣ 線対称の図形を見つけるコツ
✅ 左右対称になっているか? → 折りたたんでピッタリ重なるか考える!
✅ 対称の軸を探す! → 長方形なら縦横、正三角形なら3本など確認!
2️⃣ 点対称の図形を見つけるコツ
✅ 180°回転させても同じ形になるか? → ひっくり返しても形が変わらないかチェック!
✅ 対称の中心を探す! → 中心があるかどうかを確認!
まとめ
✅ 線対称とは?
👉 ある1本の線(対称の軸)で折りたたんだときに左右がピッタリ重なる図形!
✅ 点対称とは?
👉 ある1つの点(対称の中心)を180°回転させると元の形と重なる図形!
✅ 代表的な図形
- 線対称 → 正方形・長方形・正三角形・円 など
- 点対称 → 正方形・ひし形・ZやSの形のアルファベット など
さいごに
線対称や点対称は、 鏡に映したような形をイメージする とわかりやすくなります!
「この図形は線対称かな?」
「点対称の図形ってどんなものがある?」
と、身の回りのものを探してみるのもいいですね!
次回のブログもお楽しみに!
算数好きあつまれ〜!📏✏️
京の算数学 解答#982




