アイデア数理塾 今日の問題#124
今日のコラム
高校野球も春季大会面白かったですね〜
それにしても大阪のレベルが高い^^;
恐ろしいわ^^;
地元京都は決勝が西城陽と東山の珍しい組み合わせ。
東山は龍谷大平安にようやくリベンジを果たした。
そういえばトーナメント表見てると学校数減ったな〜と実感。
合同チームでの出場も増えてるし、調べてみると1982年の32万人だった野球人口は年々減少し、2020年には18万7000人にまで減少している。
少年野球も僕たちが現役の時では強豪だったチームが人数不足で合併していたりするし、2日前のニュースでは２１世紀枠で甲子園に出場し１勝を挙げた宮崎県の一迫商高校も廃部になった事が報じられた。
いろんな時代背景があるにせよ個人的には昔ながらのチームがどんどん減っていることにちょっと寂しさを感じています^^
さて！今日は高校数学で学ぶ内分・外分のお話です。
内分について
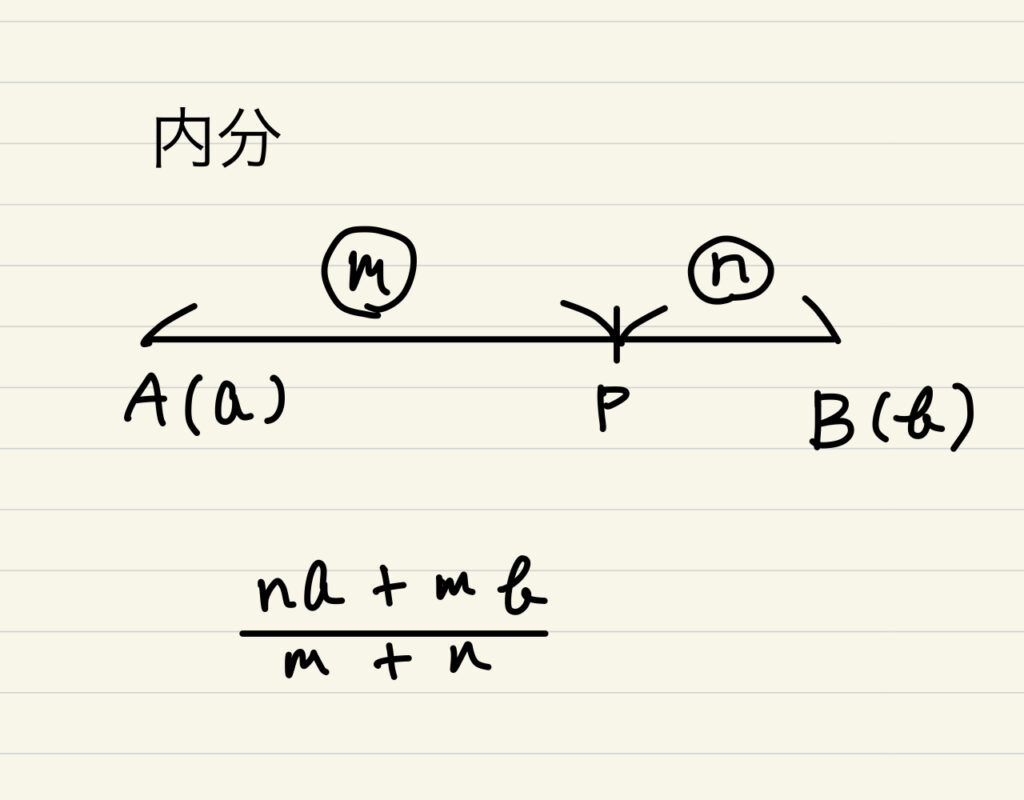
内分とは線分AB上の点PについてAP:PB=m:nが成り立つ時、点Pは線分ABを内分するという。
数学Ⅱの範囲では座標を用いて内分を計算する。
例題：A(-4)、B(2)のとき線分ABを3:2に内分する点Pを求めよ。
公式で求めるなら
こんな感じ。
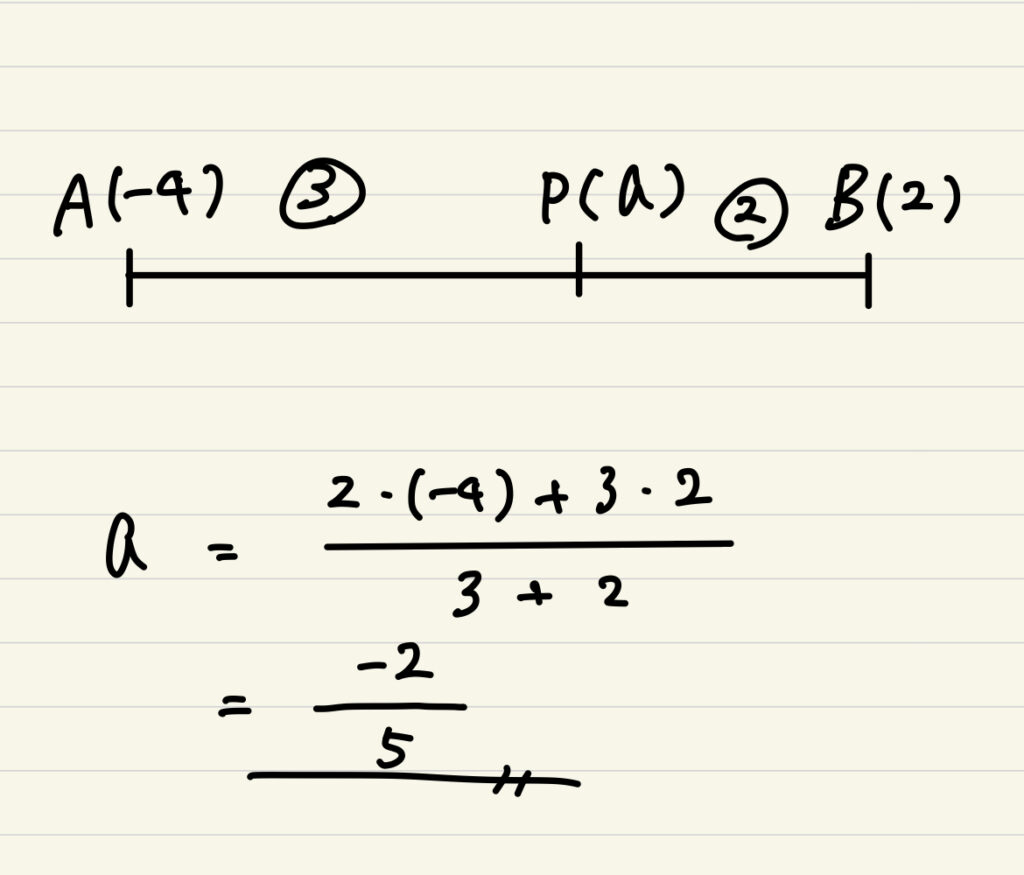
公式というのは非常に便利で数がめちゃくちゃ複雑だったり大きかったとしても、簡単に求める事ができる。
でも公式を丸覚えするのって結構苦痛だったりする。
今回は公式を使わず別の方法で求めてみよう。
この場合AからBまでは６離れているので、線分を3:2で内分すると、18/5:12/5とする事ができる。つまり、A(-4)から+18/5移動したところが点Pなので上記のやり方で求められる。
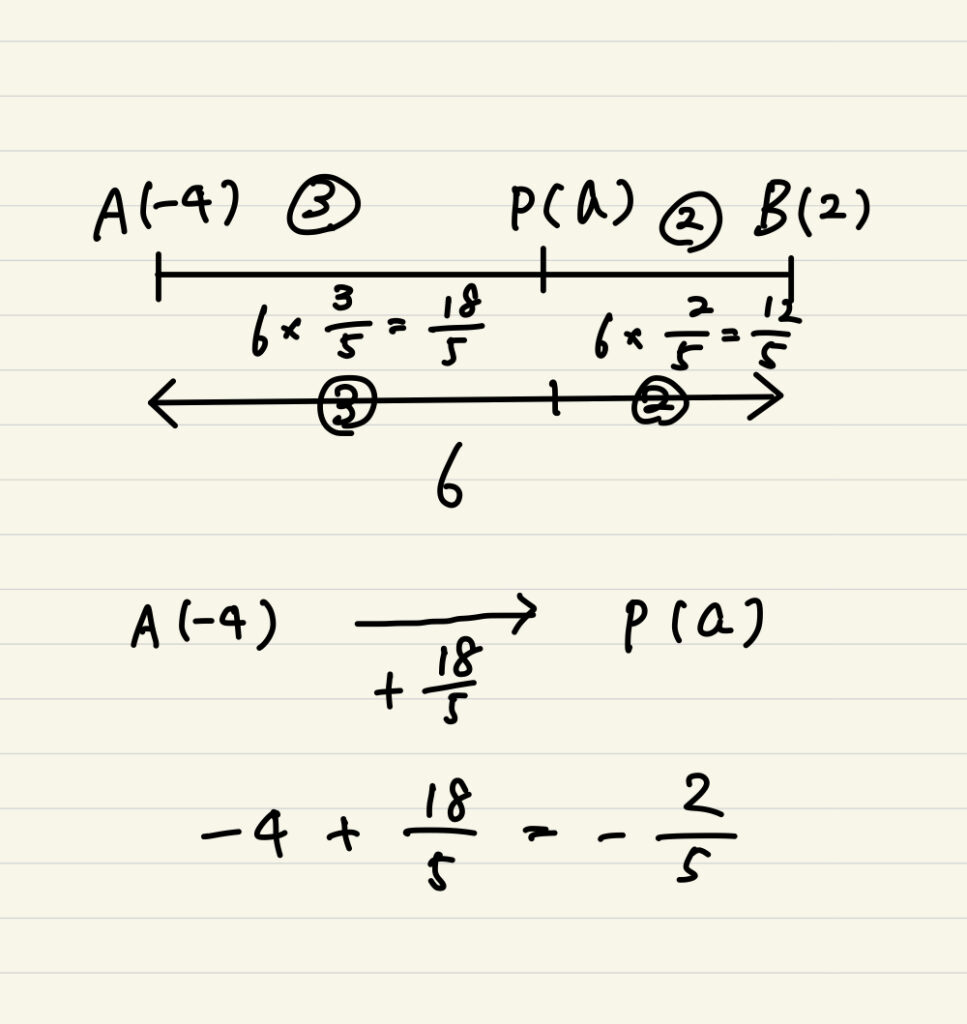
このやり方って実は公式を知らない中学生でもできる。
だけど結構複雑な計算になる事が多いのがデメリット。
公式のイメージが掴みにくい場合はこの考え方を理解しておくと公式の使い方や理解が深まるので一度チャレンジしてみてほしい。
外分について
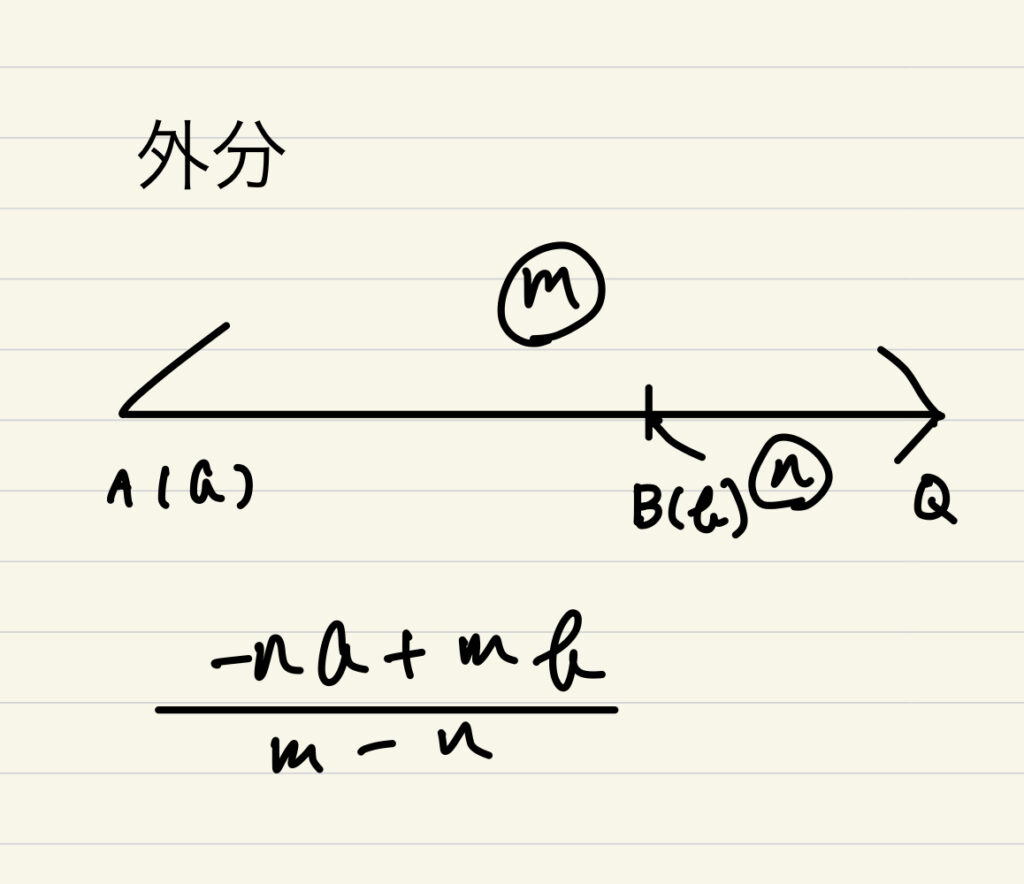
線分ABの延長上の点Qについて、AQ:QB=m:nが成り立つ時、点Qは線分ABをm:nに外分するという。
例題：A(-1)B(3)の時、3:1に外分ける点Qを求めよ
内分の時と同じように公式に当てはめるとすぐに解ける。
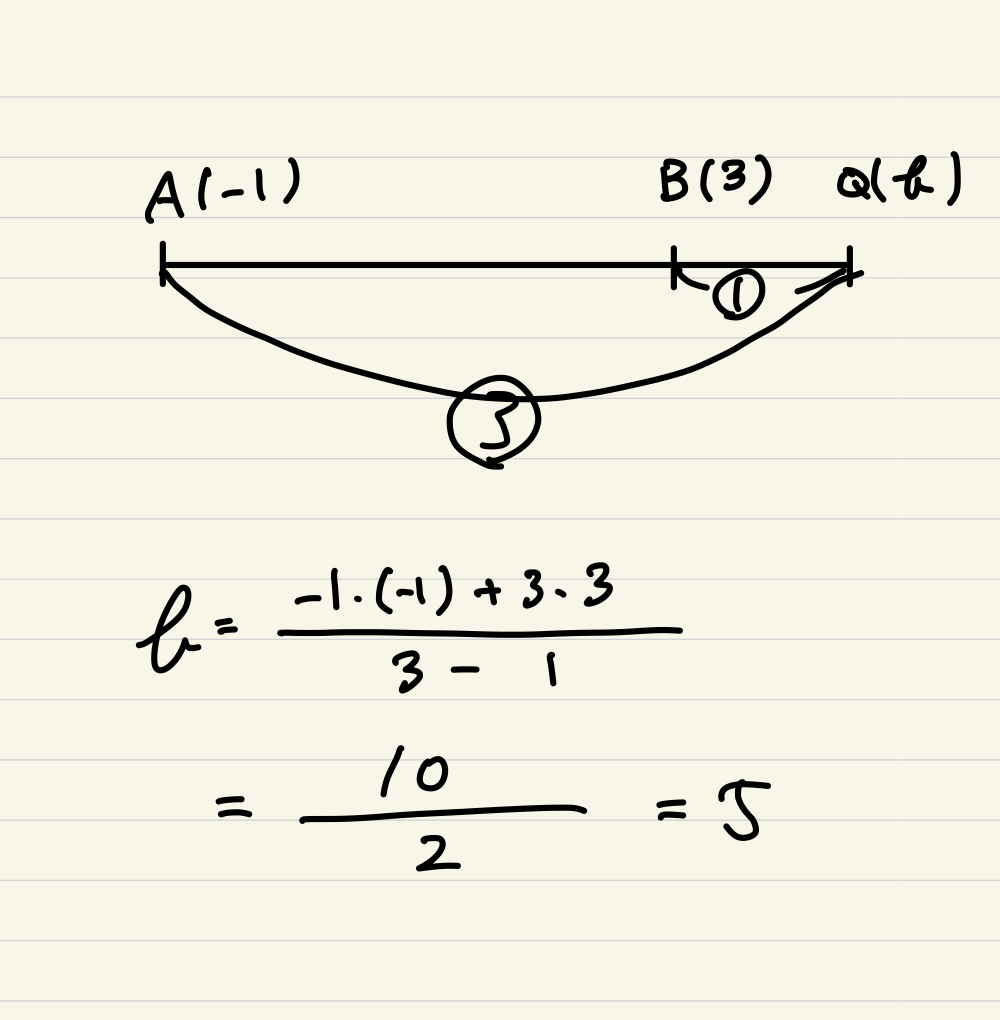
では同じように長さで考えてみよう！
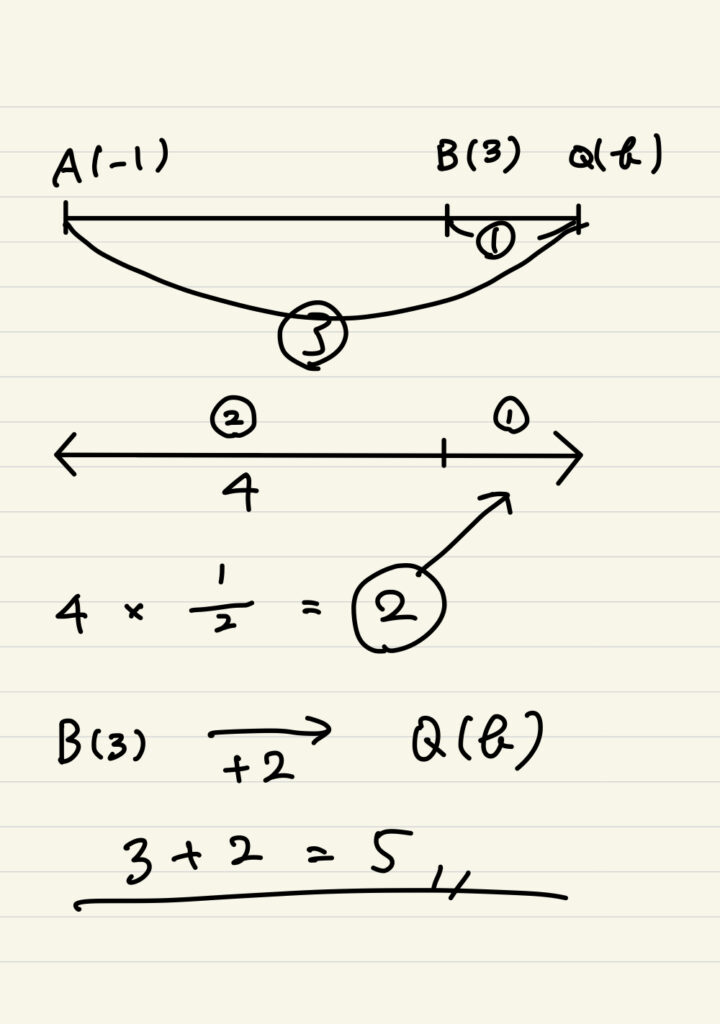
このように線分ABを3:1に外分するとは言い換えると線分AQを2:1に内分するという意味だ。この手の計算問題は図がなく文章で出題される事が多いので公式だけを覚えていたのでは意味がない。
応用を効かせるためには頭の中でこのイメージができるか？というのが大事です。
以上！京都市中京区のアイデア数理塾 油谷がお届けいたしました！
今日の解答#124
