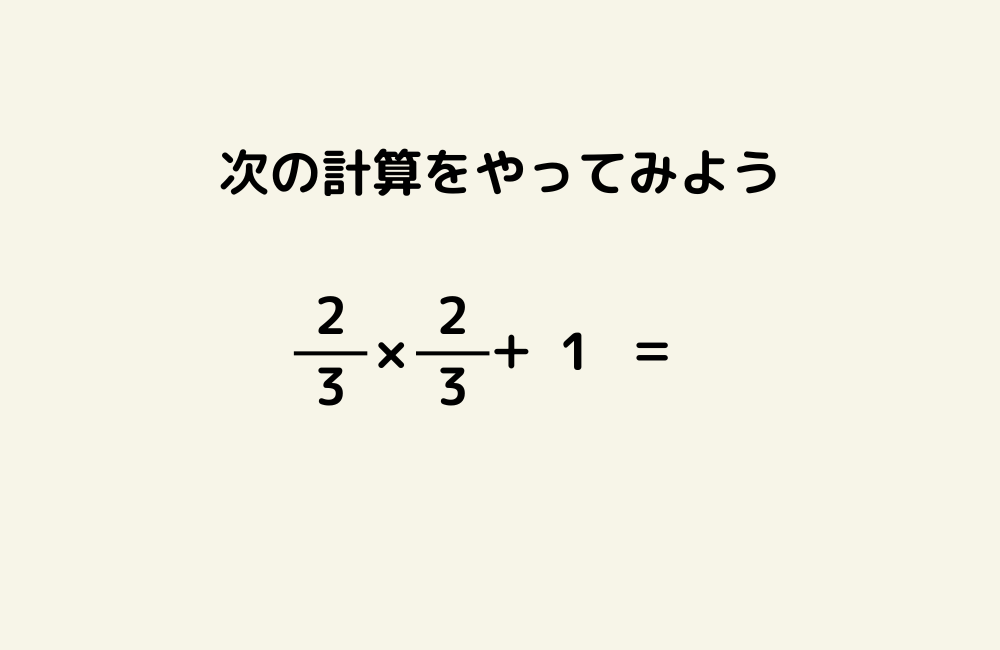数学コラムの目次
京の算数学問題#1009
アイデア数理塾はこちら
算数学コラム
小学6年生の算数は 中学数学へ進むための大切なステップ です。
特に 分数の四則計算・比・円の面積 などは今後の学習にもつながる重要単元です。
また、「線対称・点対称」「場合の数」など、図形や思考力を使う問題にも取り組みます。
この時期につまずいてしまうと、中学数学で苦労することになるため、
「どこでつまずくのか?」「どう指導すれば理解できるのか?」 をしっかり把握することが大切です。
そこで、本記事では 小学6年生がつまずきやすいポイントと、その克服法(具体的な指導法) を詳しく解説します!
1. 点対称と線対称|図形の対称性を理解する
つまずきやすいポイント
- 線対称はわかるが、点対称が理解しにくい
- 対称の軸や対称の中心を間違える
- 線対称と点対称の両方を持つ図形が区別できない
効果的な指導法
1. 線対称とは?まずは身近な例から!
- 「折り紙を半分に折ったとき、ピッタリ重なるか?」 を基準に考える
- 身近な例:ハート形・アルファベットの「A」「M」「T」
2. 点対称とは?180度回転を意識する
- 「180度回転させたときに元の図形とピッタリ重なるか?」 を基準にする
- 身近な例:アルファベットの「S」「N」「Z」
3. 実際に紙に書いて、切り取って動かす
- 線対称なら折って確認!
- 点対称なら、紙の上に回転する矢印を書いて動かしてみる!
4. 線対称と点対称の両方を持つ図形を探す
- 正方形、円、アルファベットの「H」「O」 などを例にする
➡ 詳しくはこちらの記事で解説!
2. 分数の四則混合計算|計算の順序を正しく理解する
つまずきやすいポイント
- 異分母の足し算・引き算で通分を忘れる
- かけ算・わり算で約分をしないまま計算してしまう
- 整数や小数が混ざると混乱する
- 計算の順序を間違える(分数の分配法則の誤用など)
効果的な指導法
1. 計算の順序を徹底する
分数の計算は「たし算・ひき算」「かけ算・わり算」の処理が異なります。
足し算・引き算 → 通分して計算
かけ算・わり算 → そのまま計算(逆数をとる)
2. 逆数をとる理由を納得させる
「なぜ分数のわり算はひっくり返すのか?」 を、具体的な数値を使って説明することで理解が深まります。
3. 四則混合問題を解くときは「どの順番に計算をするか?」を明確にする
➡ 詳しくはこちらの記事で解説!
3. 円の面積|公式を正しく理解する
つまずきやすいポイント
- 円周と面積の公式を混同する
- おうぎ形の面積で角度の割合を使えない
- 葉っぱ型(円の重なり)の問題が苦手
効果的な指導法
1. 公式を確実に覚えさせる
- 円周の長さ = 直径 × π
- 円の面積 = 半径 × 半径 × π
2. おうぎ形の面積を「全体の何分の1か?」で考える
例えば、90°(1/4周)なら「円の面積の1/4」と考えるようにする。
3. 葉っぱ型の問題は「円の重なり」として考える
図形を分解し、「どの部分を引けばいいのか?」を明確にする。
➡ 詳しくはこちらの記事で解説!
4. 比の利用|割合との違いを意識する
つまずきやすいポイント
- 比と割合の違いがわからない
- 等しい比の計算で、どの数をそろえるべきか混乱する
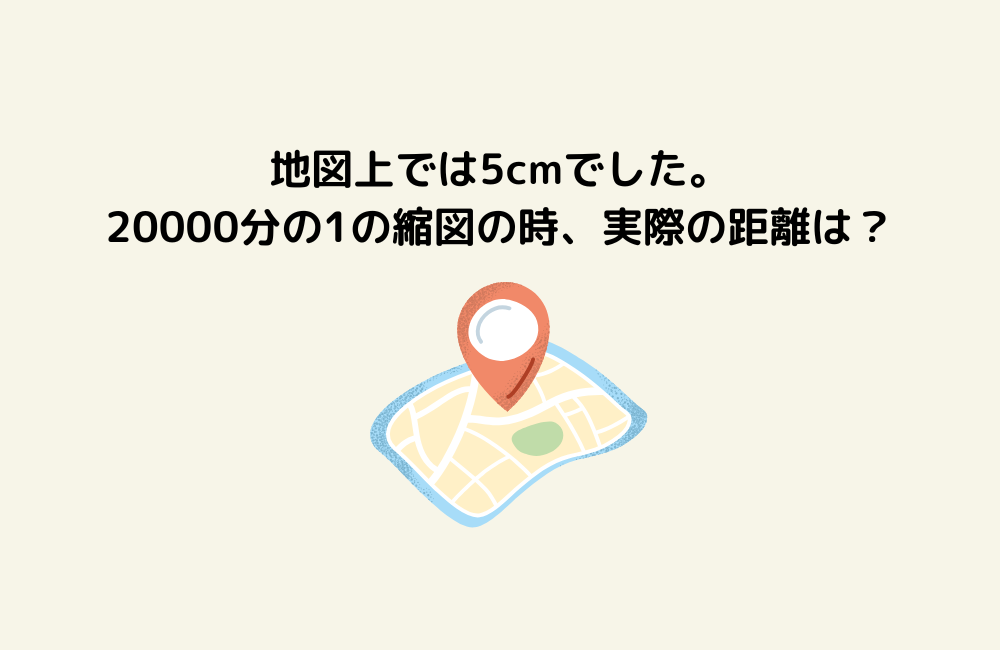
- 地図の縮尺など、応用問題が難しい
効果的な指導法
1. 割合との違いを明確にする
割合:「AはBの〇〇倍」 → 小数やパーセントで表す
比:「A:B の比」 → 割り算せずにそのまま書く
2. 比の式の扱い方を練習する
- 「3:4 = □:20」の□を求める問題では、「どちらをそろえるべきか?」を考えさせる。
➡ 詳しくはこちらの記事で解説!
5. 場合の数|整理しながら考えるクセをつける
つまずきやすいポイント
- 順列(並べ方)と組み合わせ(選び方)の違いがわからない
- 樹形図を書くのが面倒で、数え漏れが発生する
- 問題文の条件を見落としやすい
効果的な指導法
1. 順列と組み合わせの違いを明確にする
- 順列(並び方):「3人を並べる」 → 順番が大事
- 組み合わせ(選び方):「3人から2人を選ぶ」 → 順番は関係ない
2. 樹形図や表を積極的に使う
書くことを嫌がる子が多いが、 手を動かして整理することが重要 だと伝える。
➡ 詳しくはこちらの記事で解説!
6. 立体の体積と表面積|公式を丸暗記せず、意味を理解する
つまずきやすいポイント
- 体積と表面積の違いがわからない
- 公式を覚えようとして混乱する
- 展開図を描くのが苦手
効果的な指導法
1. 体積とは?まずは基本公式を統一!
- 体積 = 底面積 × 高さ
- 直方体でも円柱でもこの考え方は同じ!
- 形ごとの公式をバラバラに覚えず、基本の考え方を統一する
直方体の体積 = 縦 × 横 × 高さ
円柱の体積 = (円の面積)× 高さ
2. 表面積とは?まずは展開図で考える!
- 「展開図を描く → それぞれの面積を足す」 を徹底する
- 初めは面積を計算せず、展開図を正しく描けるようにする
3. 表面積と体積の違いを明確にする!
体積 = 中身の大きさ(どれだけの空間を占めるか)
表面積 = 表面の塗る面積(ペンキを塗るイメージ)
まとめ|小学6年生の算数を克服するポイント
計算はルールを徹底し、確実にできるようにする(分数の四則計算)
公式を正しく覚え、応用問題にも対応できるようにする(円の面積・比)
文章題や思考力を使う問題は、整理しながら考えるクセをつける(場合の数)
6年生の算数をしっかり理解することで、中学数学への準備がスムーズになります!
ぜひ、今回紹介したポイントを意識して、お子さんの学習をサポートしてください。
➡ さらに詳しく学びたい方へ!
アイデア数理塾では、お子さまの理解度に合わせた 「個別指導」 を実施しています。
ぜひ一度 無料相談 にお越しください!
京の算数学 解答#1009