数学コラムの目次
京の算数学問題#984

アイデア数理塾はこちら
算数学コラム
こんにちは!
京都市中京区で学習塾を運営している 油谷拓哉(ゆたに たくや) です。
小学6年生になると 「円の面積」 を求める公式を学びます。
しかし、こんな疑問を持つ子どもも多いです。
- 「なぜ半径を2回かけるの?」
- 「円周の公式とはどう違うの?」
- 「そもそも公式を覚えるだけでいいの?」
今日は、 円の面積の公式をしっかり理解して、確実に使いこなせるようになるための解説 をしていきます!
① 円の面積の公式
まずは、円の面積を求める公式を確認しましょう!
円の面積=半径 × 半径 × 3.14
または、 「半径の2乗 × 3.14」 とも表現できます。
公式の意味を理解しよう!
なぜこの公式になるのかを説明するために、「円を四角形に近づける方法」 を考えてみます。
② 円の面積の求め方を考える
① 円を分割して並べると?
円をたくさんのピース(扇形)に分割し、それを交互に並べると 長方形のような形 になります。
図では8等分ですがもっと細かく分けていけば限りなく長方形に近づきます。
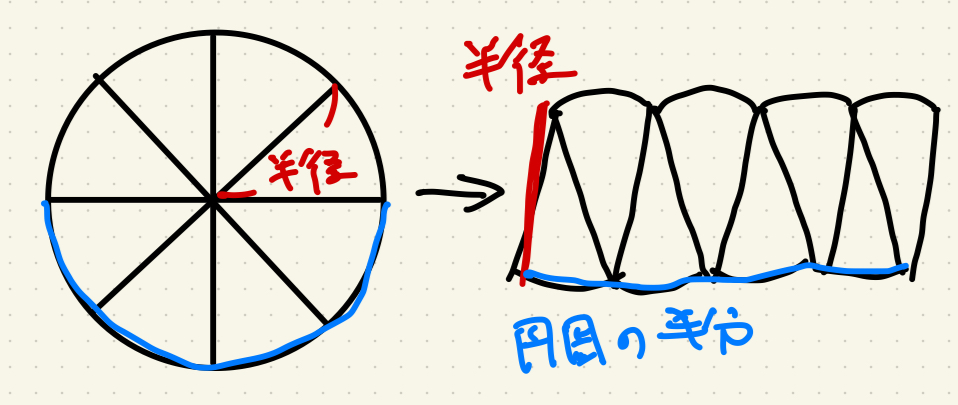
このとき、
- 長方形の「縦」は、円の半径
- 長方形の「横」は、円周の半分
となります。
長方形の面積=縦×横なので
縦=半径
横=円周の半分だから
半径×直径×3.14÷2
直径=2×半径だから
半径×2×半径×3.14÷2=半径×半径×3.14
これが 円の面積の公式の意味です!
③ 公式を使ってみよう!
では、実際に公式を使って円の面積を求めてみましょう。
例題1:半径5cmの円の面積
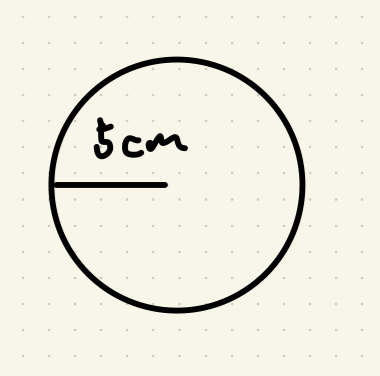
5×5×3.14= 78.5
答え:78.5 cm²
④ 直径が与えられたときの計算
円の半径が直接わかる問題は簡単ですが、
時々直径が与えられることもあります。
例題2:直径8cmの円の面積
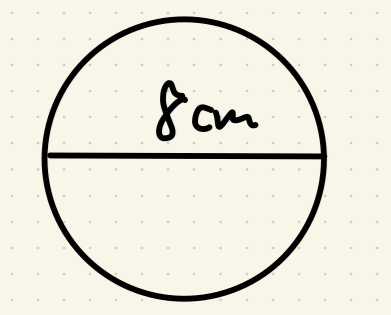
直径が8cmの場合、半径は直径の半分 なので 4cm になります。
4×4×3.14=50.24
答え:50.24 cm²
⑤面積から逆算をする問題
例題3:面積が12.56cm²の円の半径
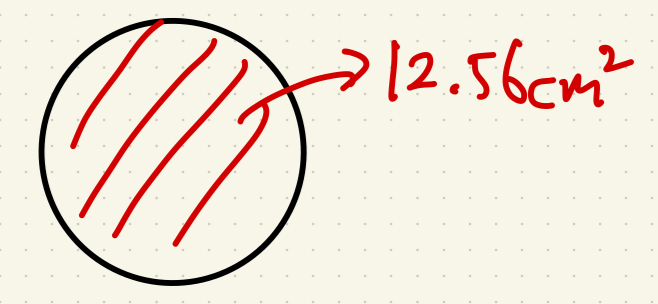
円の面積は半径×半径×3.14だから
12.56÷3.14=4cm
つまり、半径×半径=4cmなので同じ数を2回かけて4になる数字は2であるから、
答え:2cm
⑥ 応用問題:円の一部の面積を求める(おうぎ形)
円の半分 や4分の1の面積を求める問題も出題されます。
例題4:半径6cmの円の半分の面積
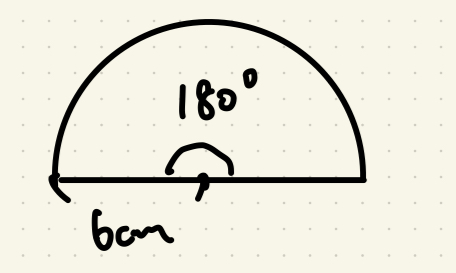
- まず円の面積を求める
6×6×3.14=113.04
- その半分を求める
113.04÷2=56.52
答え:56.52 cm²
⑥ 円周の求め方との違い
円の面積の公式と 円周を求める公式 を混同してしまう子も多いので、ここで違いを整理しておきます!
| 計算の種類 | 公式 |
| 円の面積 | 半径 × 半径 × 3.14 |
| 円周 | 直径 × 3.14 |
円周は「長さ」 を求める公式、
円の面積は「広さ」 を求める公式です。
⑦ まとめ
1. 円の面積の公式
半径×半径×3.14半径 × 半径 × 3.14
2. 直径が与えられたら半径にする
- 直径 ÷ 2 = 半径
3. 円の一部の面積を求めるときは、全体の面積を出してから計算
- 半円なら÷2、4分の1なら÷4
4. 円周の公式と混同しない!
- 円周=直径 × 3.14
- 円の面積=半径 × 半径 × 3.14
さいごに
円の面積を求める公式は 丸暗記するのではなく、「なぜこの公式になるのか?」を理解することが大切 です!
実際に問題を解いてみると 「半径を2回かける」 ことの意味が見えてくるので、
まずは 基本的な問題からたくさん解いてみること をおすすめします。
円の面積をしっかりマスターして、苦手意識をなくしましょう!
京の算数学 解答#984




