アイデア数理塾 数学コラムの目次
京の算数学問題#728
算数学コラム
みなさんこんにちは！京都市中京区で塾を運営しております。油谷拓哉（ゆたに たくや）です！
確率においてよく戸惑うのが言い回しです。
数学には“かつ”や“または“など言葉の理解をしないと解けない問題も多々出題されます。
今日は高校数学においての確率の言い回しについてお話ししていきます。
「同様に確からしい」の意味とは？
同様に確からしいとは確率の意味でどの事象も同じ確率で起こるという意味です。
例えばサイコロの目は6個ありそれぞ１回投げて目が出る確率は1/6になるはずです。
ですが、本当はサイコロの目の削り方はそれぞれ異なりますので出やすさという意味では偏るはずです。
そこで同様に確からしいとすることによって問題として理解しやすい形にしているのです。
言い換えれば全ての目が出る確率は等しいものとして考えよう！です。
“かつ”と“または”の違い
ベン図を書くとわかりやすいのですが、
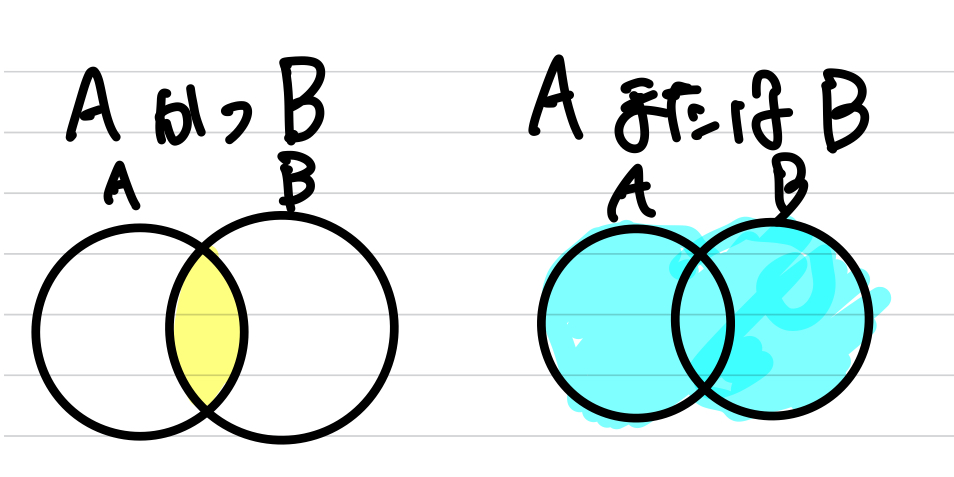
“AかつB“とは、AとBの共通部分です。
例えば、Aが2の倍数でBが3の倍数だとすると、AかつBとは２の倍数でも３の倍数でもある６の倍数ということがわかります。
“AまたはB”とはAとBの和集合です。
つまり、2の倍数でも良いし、3の倍数でもいいのです。もしくはその両方でも構いません。
何を指しているか？は図で覚えてしまいましょう！
少なくとも〜の意味
少なくともとは別に１回でも良いし２回でも良いし回数は問わないが１回は指定の事象が起こることを言います。
例えばコインを3回少なくとも１回は表が出る確率を求めたとします。
その場合、①表が１回出る場合②２回出る場合③３回出る場合と場合分けをする必要がありますが、面倒臭いですよね。
そんなときは逆を考えます。
少なくとも１回は表が出るの逆は「１度も表が出ない」となります。
表が１度も出ない確率は1/8ですので、確率の全体を表す1―1/8＝7/8が答えとなります。
少なくともが問題文に書いてあるときは「まず逆を考えて全体から引く」と考えましょう！
“選ぶ“と“並べる“の違い
場合の数の単元で学ぶ順列Pと組み合わせCです。
この２つの見分け方は並べるのが順列、選ぶのが組み合わせです。
PとCの使い分けが難しいと感じたときは問題文の文言に着目しましょう！
AのあとBが起こる確率
AのあとにBが起こる場合を条件付き確率と言います。
よく生徒からは「普通の確率と見分け方がわからない」と言われるのですが、
見分け方は問題文です。
Aが起こってからBが起こるというAが起こる条件下の元次のBが起こるという問題文です。
例えばAとBの工場の不良品の確率は3％と6%です。1000個のうち23個が不良品だったとすると、不良品がAである確率を求めなさい。
これは不良品を引きそれがAであるという２段階になっています。
これが条件付き確率です。
以上！京都市中京区のアイデア数理塾 油谷拓哉（ゆたに たくや）がお届けいたしました！
算数好きあつまれ〜！
京の算数学 解答#728
