アイデア数理塾 京の算数学問題#219
算数学コラム
たすきがけは因数分解の解き方の一つです。
特に高校数学ではこのたすきがけでの因数分解は基本問題になりますのでこのブログで完全攻略してしまいましょう！
たすきがけとは？
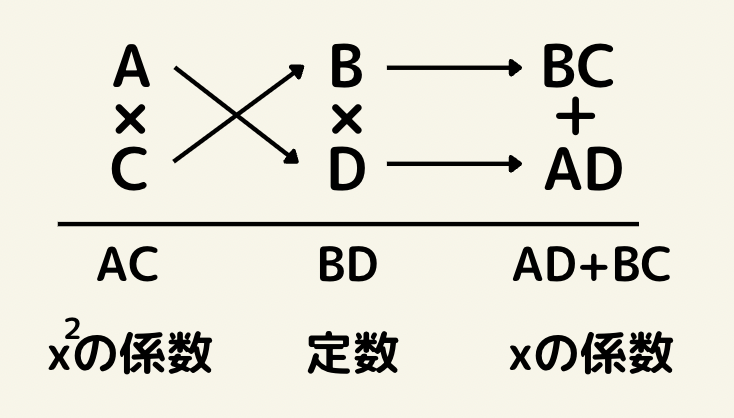
x^2の係数と定数項の因数の組み合わせパターンを考えその中でかけ合わせてBCとADを作りBC+AD＝xの係数になるパターンを考えていきます。
なぜそうなるの？
例えばax^2+bx+cを因数分解したとしたら。
因数分解した後の形は係数は不明ですが(Ax+B)(Cx+D)の形となるはずですよね。
※係数や項をABCDと仮置きしただけです。
この式を展開した時、ACx^2 + (AD+BC)x + BD となります。
と言う事は、元の式のaにあたるものがACです。
同様にまとめると
a=AC
b=AD+BC
c=BD
となります。
つまりここからたすきがけの決まりが導き出せます。
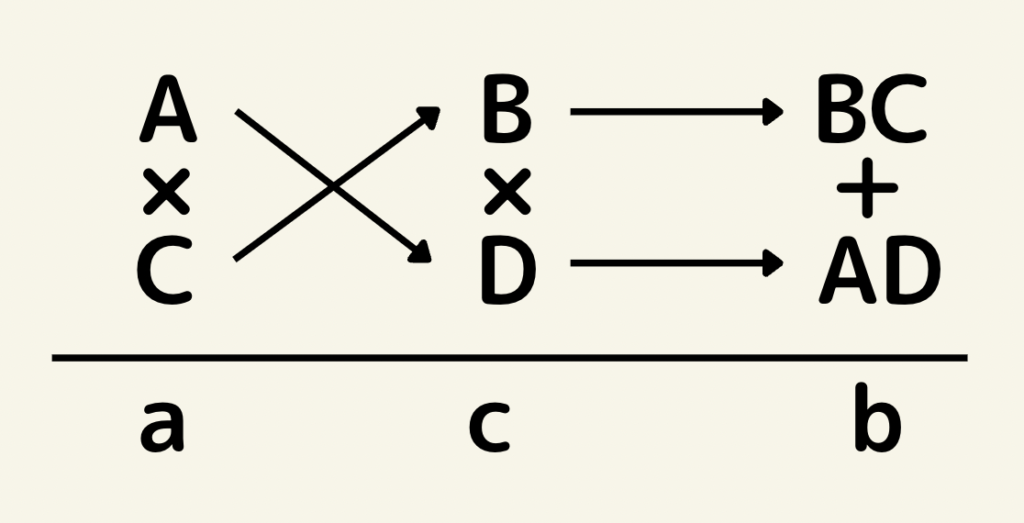
つまり因数分解のたすきがけとは、因数分解が出来たと仮定した時の係数を比較して導き出されたものという事です。
因数分解たすきがけの問題を解いてみよう！
基本問題編
次の式をたすきがけで因数分解しましょう！
※x^2とはxの二乗を意味する
（１）6x^2+7x+3
（２）2x^2+5x-3
（３）8x^2+6xy-5y^2
【解答】
（１）
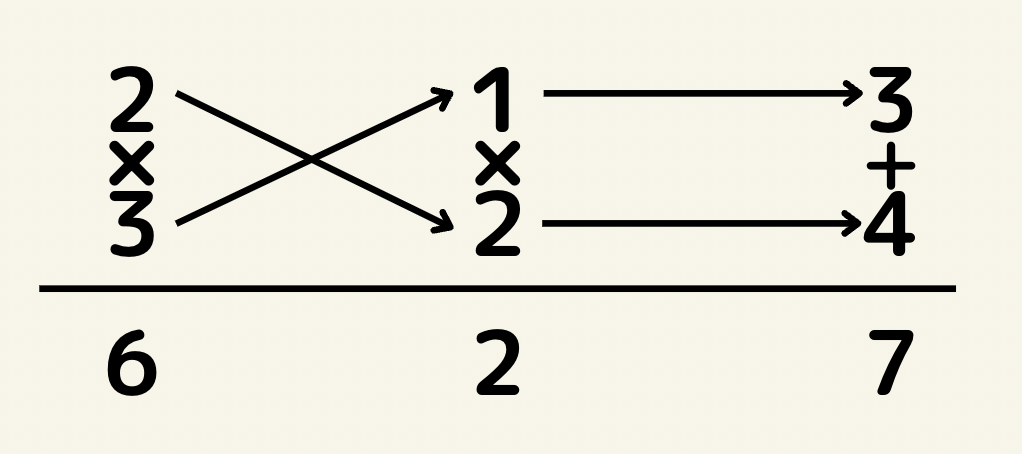
よって(2x+1)(3x+2)
（２）
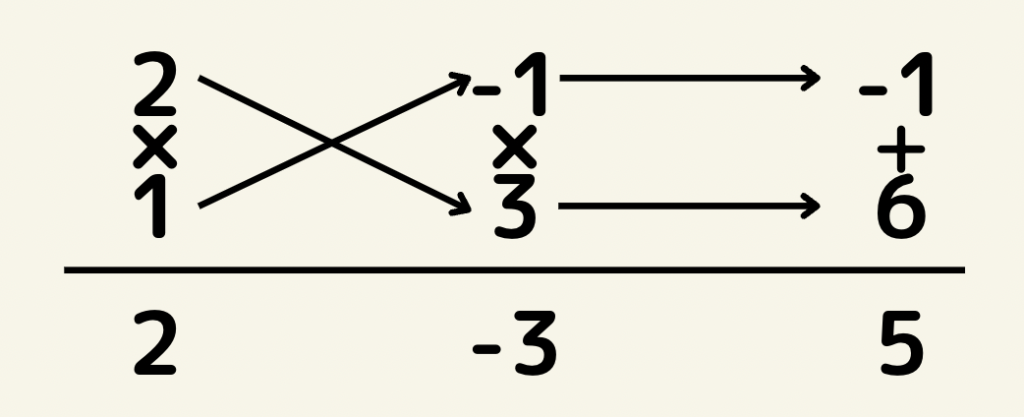
よって(2x-1)(x+3)
（３）
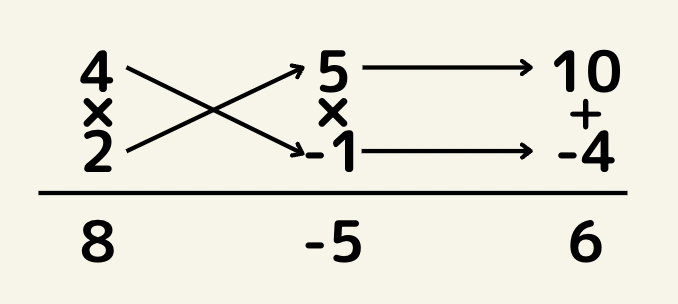
よって(4x+5y)(2x-y)
応用問題編
次の式をたすきがけで因数分解しましょう！
2x^2+xy+4x-y^2+y+2
【解答】
2x^2+xy+4x-y^2+y+2をxについて整理すると
2x^2+(y+4)x-(y+1)(y-2)になる。
たすきがけをすると
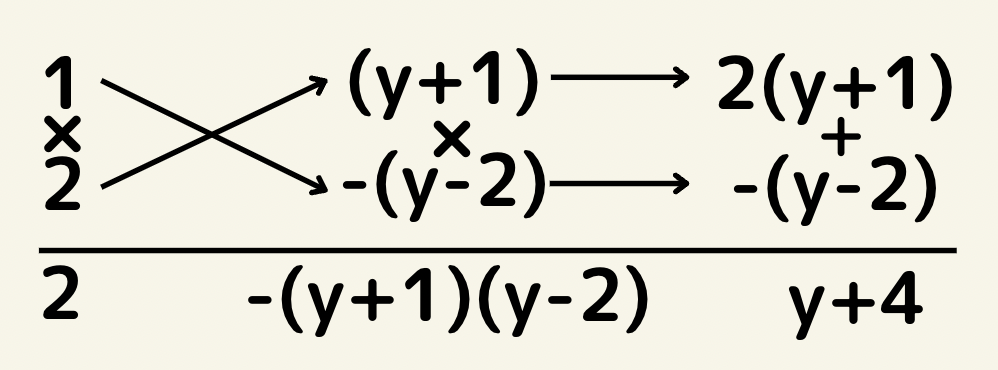
よって(x+y+1)(x-y+2)となる。
このように高校で習う因数分解では因数を数字ではなく(y+1)のような形でたすきがけを行う場合もあるので注意しよう！
ただ、きちんと学べば簡単にできるようになるので繰り返し勉強していきましょう！
以上！京都市中京区にあるアイデア数理塾、油谷がお届けいたしました！
京の算数学 解答#219
