数学コラムの目次
京の算数学問題#657

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
今は空前の中学受験ブームと言えます。
地域によっては私学無償化になり、コロナ禍の対応以降中学受験は非常に人気になっています。そんな中で中学受験算数といえば「特殊算」と呼ばれる通常授業ではやらないが受験では頻出になる計算方式が重要になってきます。
ですが特殊算のやりすぎで方程式が苦手になってしまうお子さんもいます。
今日はそんなおはなしです。
和差算で考えてみる
例えば京の算数学問題「Aくんのクラスは30人で男子は女子より6人多い。男子と女子の人数は?」に対して、特殊算と方程式両方で考えてみましょう。
特殊算
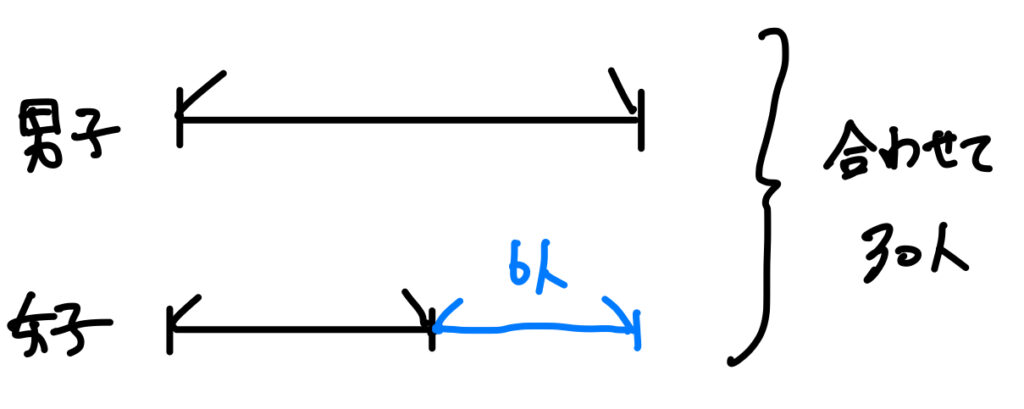
※青で書かれている6人は30人には含まれません
男子の人数+女子の人数=30人です。
つまり男子の人数=女子の人数+6人であると言えます。
と言うことは30人+6人が男子の人数の2倍になります。
よって男子の人数は(30+6)÷2=18人になります。
同様に女子の人数=男子の人数−6人となりますので、
30人−6人=24人が女子の2倍の人数になります。
よって女子の人数は(30-6)÷2=12人が答えになります。
方程式で考える
方程式の場合、男子の人数をx人とおきます。
女子の人数は30-x人なので、方程式を立てると、
30-x=x-6となり、2x=36 x=18となり男子の人数がわかる。
つまり女子は30-18=12人となる。
連立方程式で考えてみる
中学2年で学ぶ連立方程式の場合、男子の人数をx人、女子の人数をy人とします。
男女の生徒数の合計は30人なので
x+y=30
男子と女子の生徒数の差は6人なので、
x-y=6
これらを連立して解くと、
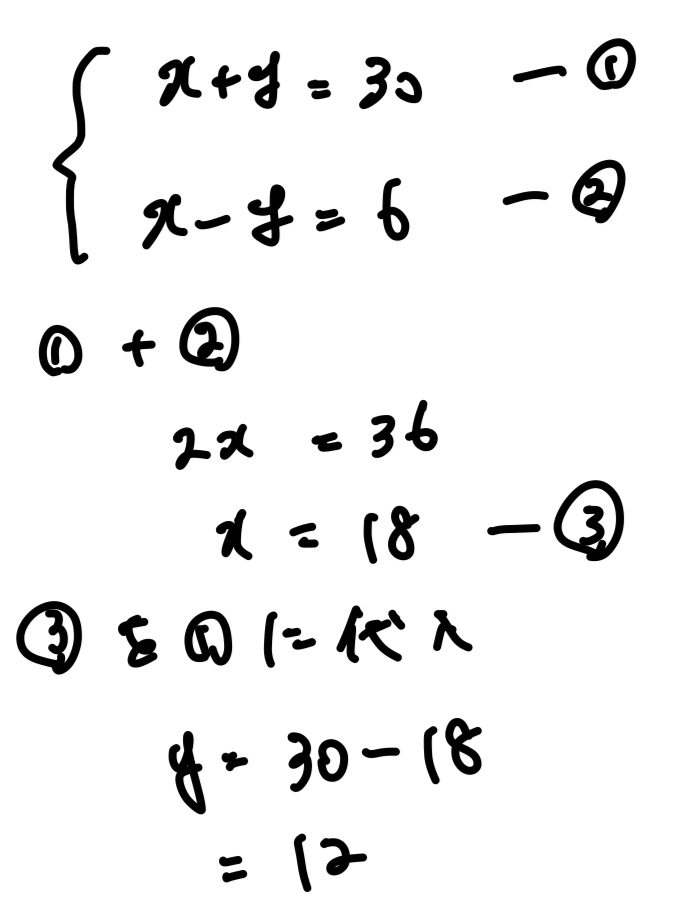
X=18,y=12となるので、男子は18人、女子は12人ということがわかる。
なぜ特殊算で方程式が苦手になるのか?
中学受験では特殊算をテクニックとして学ぶところが多いです。
ですので解けたらOKとなります。
中学になると方程式で解けや連立方程式で解けなど問題文に解き方の指示が書いてある場合が多いです。
ですが中には中学受験でやったから方程式使わなくてもとけるじゃん!とそのまま解いてしまう生徒もいます。
本来数学の学びとは同じ答えになるもので合ってもさまざまな解き方を学び、どの解き方でも解けるようにする事が求められます。
つまり答えは合っていても問題の意図と異なるので解答としては間違いになるのです。
特殊算の意味は理解しづらい
一方で特殊算の理解はなかなか難しいものがあります。
特に成長過程である小学生はまだ脳も発達段階です。
つまり理屈は理解できていないけど解けると言う現象に陥りやすいのです。
私は中学受験を経て中学生になった生徒には必ず「特殊算は捨てましょう」と言います。
もちろんテクニックとしても理論としても特殊算は素晴らしいものがあるのですが、捨てなさいと極端な指示を出さないと子どもたちにはなかなか伝わらないところがあるのです。
意図がわかるのはその先、今は理由よりもこうした方がいいよと道筋を提示することも大切なことなのです。
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#657




