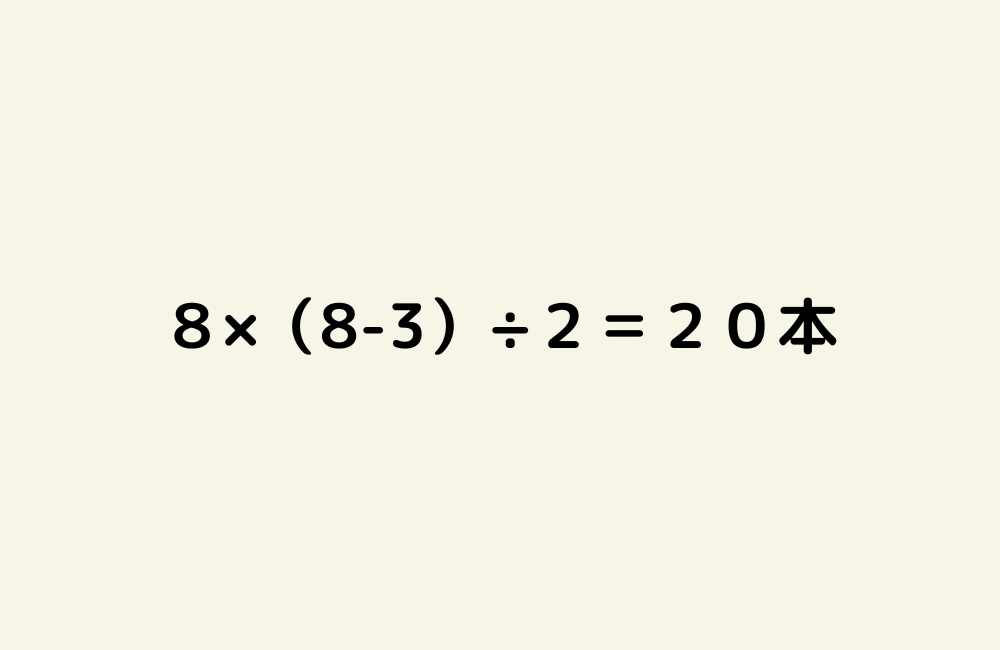数学コラムの目次
今日の数学問題#377

数学コラム
みなさんこんにちは!京都市中京区で学習塾を運営しております。ゆたに たくやです!
京都府公立高校の2023年の入試も前期が終了しました。
当塾の受験生たちもすごく不安な様子で当日を迎えました。
私もドキドキですが、きっと良い結果が出るんじゃないかな?とそんな気がしています。
今日のブログは京都府公立高校の前期数学を解いてみたので総評を書いていこうと思います。
問題は公開されていますのでそちらをご確認ください。
今回は難易度やや難しいレベル
今回は特に平面図形が難しいと感じた。
照明の段階から書き方に困った生徒は多かったはずです。
比も複雑な数字になるのでこれであってるの?と思ってしまう受験生が多そう。
規則性はプログラミング。これも流行りだろうなという印象。
個人的には面白かったけれど、中学入試にも出てきそうな問題^^;
関数の問題も少しひねった出題の印象。
全体的にやや難しいなというレベルだった。
大問1 計算ミスさえしなければ、、、
例年通り計算ミスをしなければなんとかなる。
気になるのは(5)の変化の割合の求め方。きちんと定理が理解できていれば解けるのだが、計算ミスも増えそうな印象。(8)も単純な角度を求める問題ではなく、内角の和を使ったり、補助線を引いたりなど苦手な受験生は多そう。これは例年より難しいと感じた。(9)くじを区別しないという視点が解釈できているか?単純に樹形図書けばOK。
大問2 統計の仕組みをどれだけ理解できているか?
(1)の時点でかたまってしまう受験生がいそう。純粋に方程式を立てるのではなく、aとbの組み合わせを考えていく必要がある。
これが突破できれば(2)もスムーズに解けそう
大問3 立体として捉え平面として捉える
正八面体の図を見るときに立体として捉える場合と平面として捉える見方が必要になる。
例えばABFDは正方形である。
この見方ができるかどうか?
ただ比較的空間図形は例年よりも簡単な印象。
複雑な考え方さえしなければ特に(3)まで苦なく解けそう。
大問4 面積中心の関数問題
今回は結構珍しいなと思いました。
どちらも面積をベースに問われる問題です。
(1)は問題なく解けると思います。(2)に関してはやや難しいレベルだと思います。
(2)は点Fを仮置きしてそれぞれの面積の関係性に目星を付けたらいけるがここは時間がかかりそう。
大問5 今回の最大難問
今回の目玉はこれ。
(1)の段階から証明の書き方でつまづきそう。
なぜなら今回は対象移動を行うからだ。
大抵受験対策で勉強しているのは同位角などオーソドックスな相似の証明パターンですが、今回は折り返しているので対称移動を行う。それも2回も折り返しているので余計にイメージがしにくい。
(2)3:4:5に気づけるのか?二等辺三角形に気づけるか?がポイント。でもこの時点で難しい。せめて1:2:√3にしてくれ^^;
(3)最大難問これできたらマジすごい。補助線引けば一発なんだけど、そこに至るまでの過程と求める比が結構鬼畜なので、計算ミスも多そう。
大問6 プログラミングの規則性
規則性でプログラミングを使うのは面白い。
解いていて面白かったが(1)は数えるだけでOK。ここは落とせない。
(1)は階差数列に気づけるか?がポイント。これさえ気づければ解ける。
(2)は上+左+下―右=左+下になる事が気づけるか?がポイント。
矢印を4方向ごとに法則性を見つけ組み合わせるのは結構しんどいかも。
実際解いてみて感じたのは、全体的に公式に当てはめて終わり!のパターンと組み合わせを考えるパターンが明確に分かれているような印象でした。
全体的に難しい!という印象ではなく、メリハリが効いている構成だなと思いました。
受験生の皆様お疲れ様でした!
以上!京都市中京区のアイデア数理塾 ゆたに たくやがお届けいたしました!
今日の数学 解答#377