数学コラムの目次
京の算数学問題#221

京の算数学コラム
今日は因数分解の応用問題をまとめていきます。
公式をただ覚えるだけでなく使えるようにするためには置き換えの問題や2回因数分解をするタイプの問題は非常に有効です。
ぜひチャレンジしてみましょう!
置き換えの因数分解
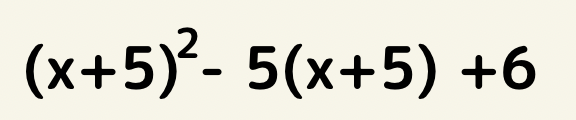
(x+5)=Aと置くと
A^2 -5A +6となります。
因数分解すると(A-2)(A-3)となり、
A=x+5を代入すると
(x+5-2)(x+5-3)=(x+3)(x+2)になる。
この置き換えの因数分解は入試の頻出問題ですのでぜひ押さえておきましょう!
共通因数をくくり出してから行う因数分解
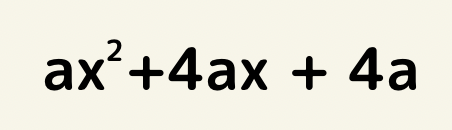
共通因数はaなのでaで括ると
a(x^2 + 4x +4) さらに因数分解すると
a(x+2)^2となる。
一度共通因数をくくりだし、因数分解の公式を使って因数分解をする2回因数分解するパターンの問題です。
1つの文字について整理してから行う因数分解
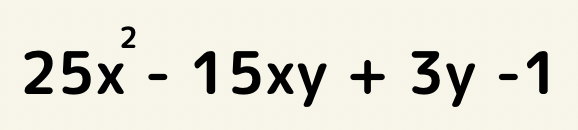
文字の次数を比較し一番次数の低い文字について整理する。
今回はyについて整理をする。(yだけを文字ととらえる)
-3(5x-1)y+25x^2-1
=-3(5x-1)y+(5x+1)(5x-1)
ここでA=5x-1とすると、
=-3Ay+A(5x+1)
=A(-3y+5x+1)
=(5x-1)(5x-3y+1)になる。
対称式の因数分解
対称式とは、x+y=y+xのように文字を入れ替えても答えが変わらない式の事です。
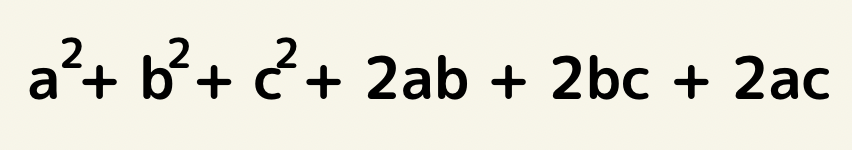
まずは同じ文字(今回はa)について整理をしてみましょう。
a^2 + 2(b+c)a + (b^2 + 2bc + c^2)となります。
a^2 +2(b+c)a + (b+c)^2と因数分解できるので、
置き換える因数分解と同様に、A=b+cとし、置き換えると
a^2 +2Aa + A^2なので
(a+A)^2となり、A=b+cを代入すると
答えは、(a+b+c)^2となる。
交代式の因数分解
交代式とはどの2つの変数を入れ替えても元の式の−1倍になる式の事です。
例えば、x-y=-(y-x)となる式の事です。
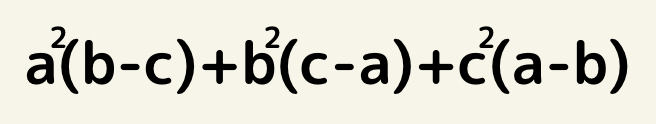
この場合も同様にaについて解いていきましょう
(b-c)a^2 + cb^2 – ab^2 + ac^2 – bc^2
=(b-c)a^2 +(c^2 – b^2)a + cb^2 – bc^2
=(b-c)a^2 – (b+c)(b-c)a + bc(b-c)
ここでA=b-cと置くと
Aa^2 – A(b+c)a + Abcで共通因数Aをくくり出すと
A{a^2 – (b+c)a + bc}
=A(a-b)(a-c)
=(b-c)(a-b)(a-c)となる。
その他の因数分解パターン
【問題】
(1)a^2+2ab+b^2-c^2
(2)(a+b+c)^2-(a+b+c)^2
(3)x^4-x^2-12
【解答】
(1)(a+b)^2-c^2 でa+b=Aとすると、A^2-c^2=(A+c)(A-c)
よって、(a+b+c)(a+b-c)
(2)a+b=Aとすると、(A+c)(A-c)=A^2-c^2
よって、(a+b+c)(a+b-c)
(3)x^2=Aとすると、A^2-A-12=(A+3)(A-4)
よって、(x^2+3)(x^2-4)=(x^2+3)(x+2)(x-2)
このように因数分解の解法パターンにはいくつかの法則があることがわかります。
文字の組み合わせを見つけてパズル感覚で取り組むと面白いですよ。
算数好きあつまれ〜!
京の算数学 解答#221



