アイデア数理塾 今日の問題#098
今日のコラム
先日のロッテ佐々木投手の完全試合未遂の件について采配に関して色々話題に上がってますが、、
そんなことより、勝った日ハムですよ！
この勝利は何回も言いますがデカいです！
野球は相手よりも1点多く取れば勝てるスポーツですので勝利の方程式は、0点に抑えて1点で勝つというのが理想系。
ただプロ野球はエンターテイメントな要素が強いので、勝つこと以上にファンへの還元が必要になってきます。新庄監督の采配は個人的には大好きですし、スモールベースボールこそ日本らしさがあって良いと思う一方で、チームとしてファンを楽しませているというより監督がファンサービスやってる感があってちょっと違和感を感じている今日この頃。
スターって難しい^^;
さて今日は数学の小話。
循環小数って知ってますか？
例えばこんなやつ
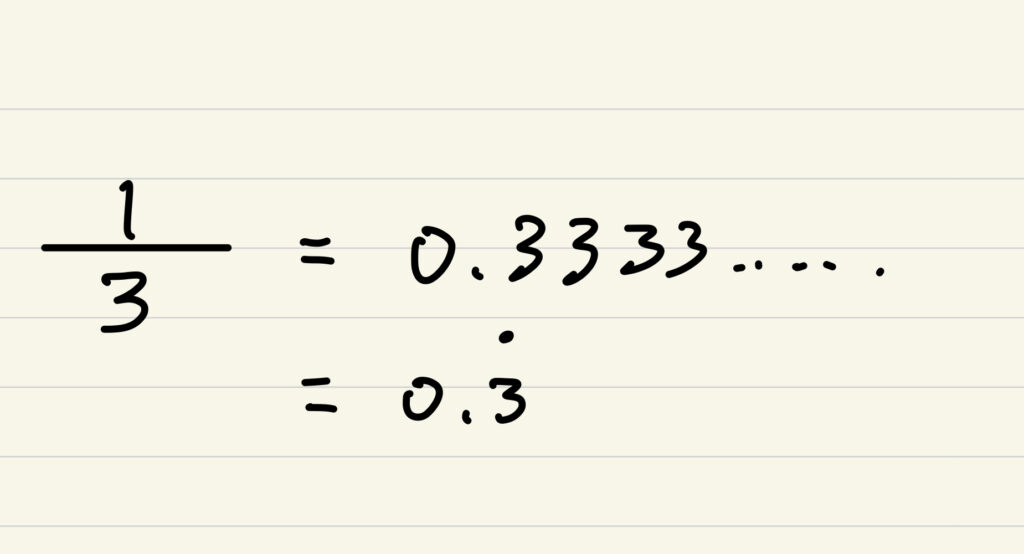
この黒丸のついている下の数字が続いていくという意味を表している。
ただここで疑問点がある。
次の問題にチャレンジしてみよう！
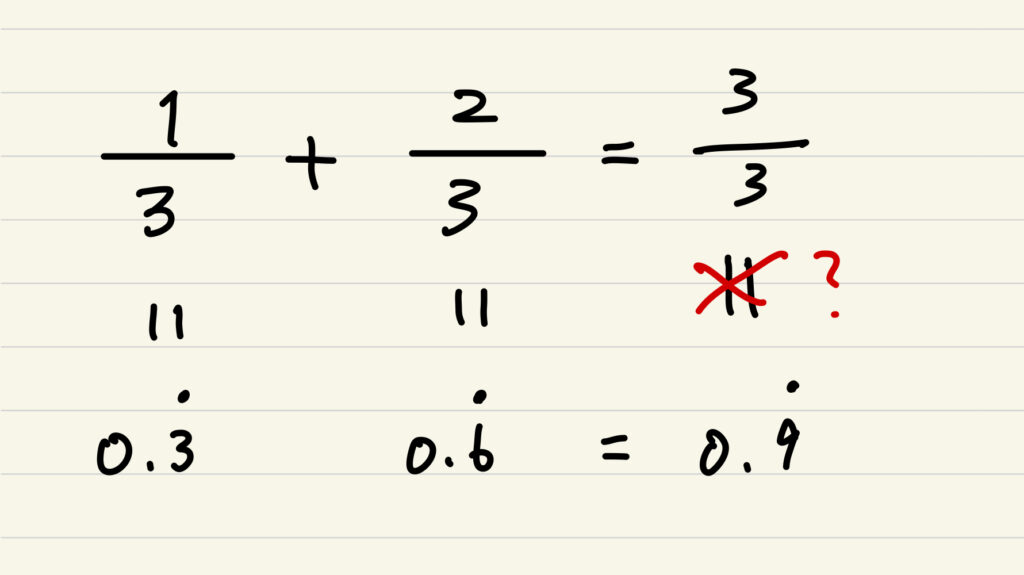
お察しの良い方はお気づきかと思いますが、1/3+2/3=3/3=1これは納得いくと思いますが、0.333333….+0.6666666….=0.9999999……
これは１ではないですよね。ということは、どういうこと？
はい。もちろん当時学生だった僕もそう思いました。
今まで＝（等号）は左辺と右辺が同じ数出ないといけないはずなのだが、限りなく１に近いとはいえ、＝じゃなくて≒じゃないのかな？なんて疑問を巡らせていました。
これを解決してくれるのが「無限等比級数」である。数Ⅲの範囲です^^;
0.999999999…..=0.9+0.09+0.009+……. と書き換えることができる。
これは初項「0.9」公比「0.1」の等比数列の合計だと言い換えることができる。
等比数列を無限に足したものを無限等比級数という。
無限等比級数は −１＜公比r＜１の時、初項/(1-r)に収束する。
収束するとはその値に限りなく近くなるという意味。
つまり、今回の例の場合はこうなる。
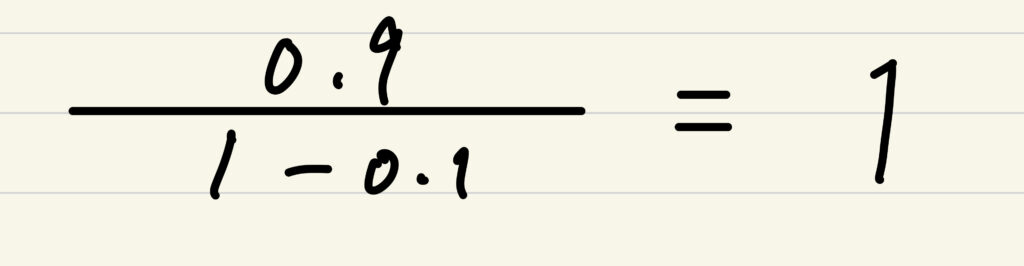
この収束するということは限りなく１だと言えるので≒ではなく＝を使うんだとか。
すごくモヤモヤしているのが余計モヤモヤした解説だったことは言うまでもない笑
以上！京都市中京区のアイデア数理塾 油谷がお届けいたしました！
今日の解答#098
