アイデア数理塾 今日の問題#093
今日のコラム
数学というと代数学（方程式などの計算分野）幾何学（図形問題）に大分される。
学校によっても、中学の時から２分割され並行して授業を進めていくクラスもある。
学校の数学という授業のキモは「数学的な思考」を身につけること。
ただ計算をするだけはなく意味を考えながら本質をとっていく。
今日は数学の基礎的特徴である分解と総合についてのお話をしていこうと思います！
分解と総合
数学の基本は分解と総合と呼ばれる2つの作用からなる。
例えば２８＋３＝３１ このような計算の場合各位ごとに分けて塊を作る必要がある。
28=(10×2)+8 ここに3を足すと 28+3=(10×2)+8+3=(10×2)+11=(10×3)+1
つまり１０の塊が３つと１の塊が１つに分解できる。
これを総合すると31になる。
この考え方は素晴らしいもので、図形に至っても多角形の内角の和を求めるためには三角形に分解する必要がある。そして三角形は辺が3つに分解できる。この辺の組み合わせを変えることで様々な図形や幾何模様が出来上がる。
世の中の発明の基本原理はこの考え方だとも言える。
ビジネスの世界でもTTP（てっていてきにぱくる）をまずやってみよう！と言われることもある。世の中の成功モデルを真似し分解し、総合して新しいものを組み立てていく。
分解と総合の考えは実は小学校の算数からやり続けているのにそれを意識していないところに問題がある。小学校の算数中学の数学をしっかり学ぶだけで社会人の基礎が出来上がるとも言えるのだ。
数的思考を鍛えるブラックボックスゲーム
ブラックボックスゲームは入口→□→出口の回路の中で何が行われているのか？を想像し解答していくものです。
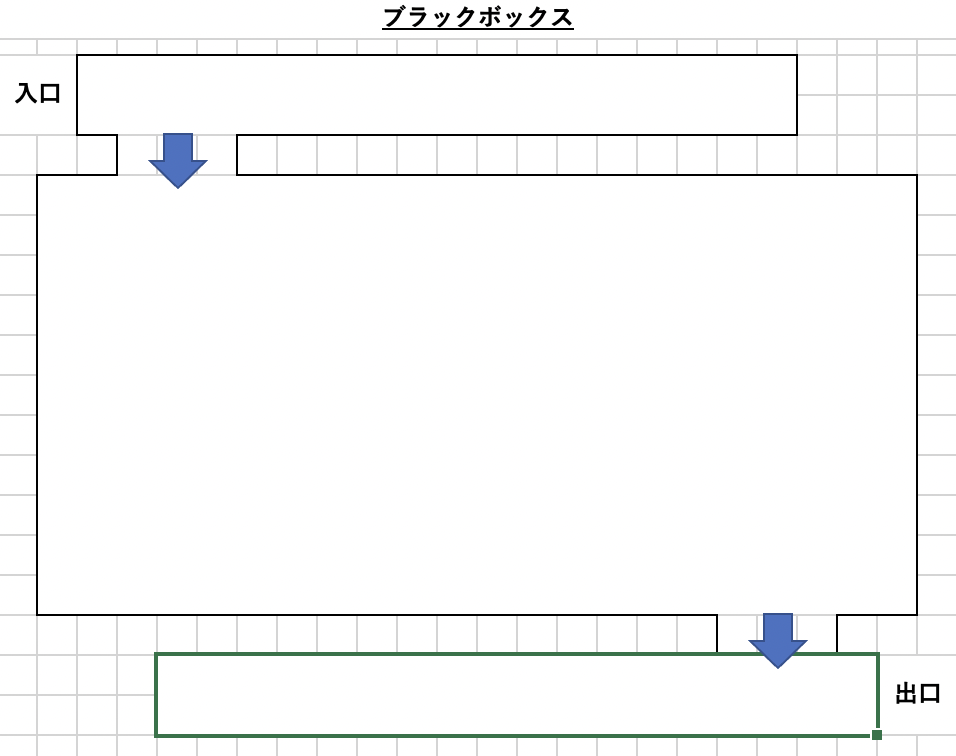
この考えは分解→総合の考えも必要であり、関数の基本的な考え方はこれになる。
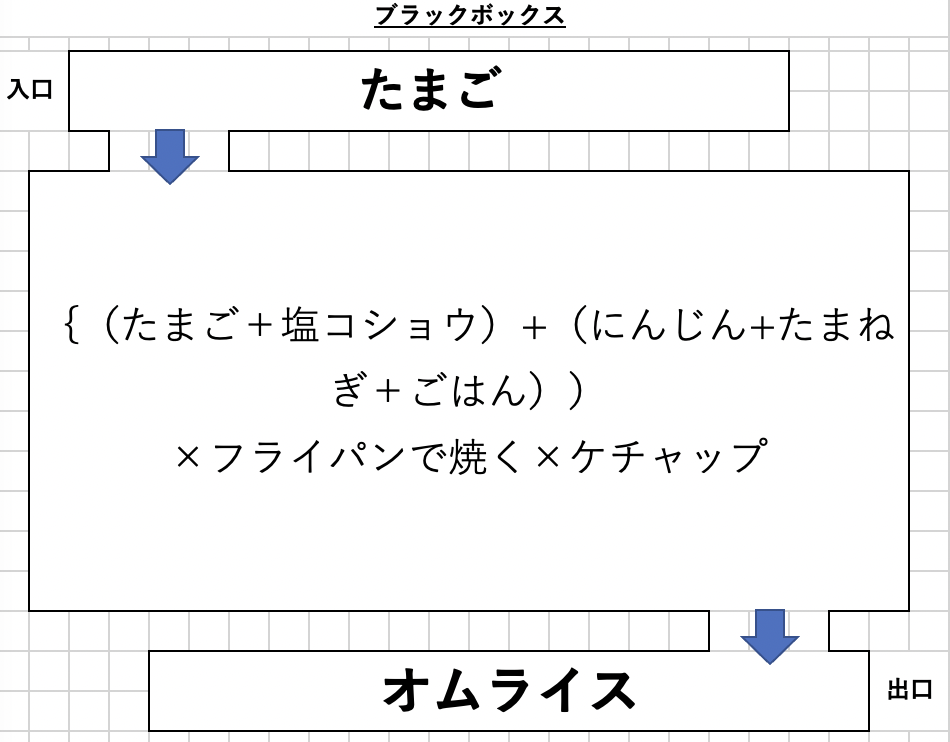
例えばたまごを入れたらおいしいオムライスが出来上がるとしよう。
それなら、（卵＋塩コショウ）と（にんじん＋たまねぎ＋ごはん）をそれぞれ炒めて卵でくるみケチャップをかけたら完成になる。
式にすると
｛（たまご＋塩コショウ）＋（にんじん＋たまねぎ＋ごはん）｝×フライパンで焼く×ケチャップ＝おいしいオムライス
こんなとこだろうか？
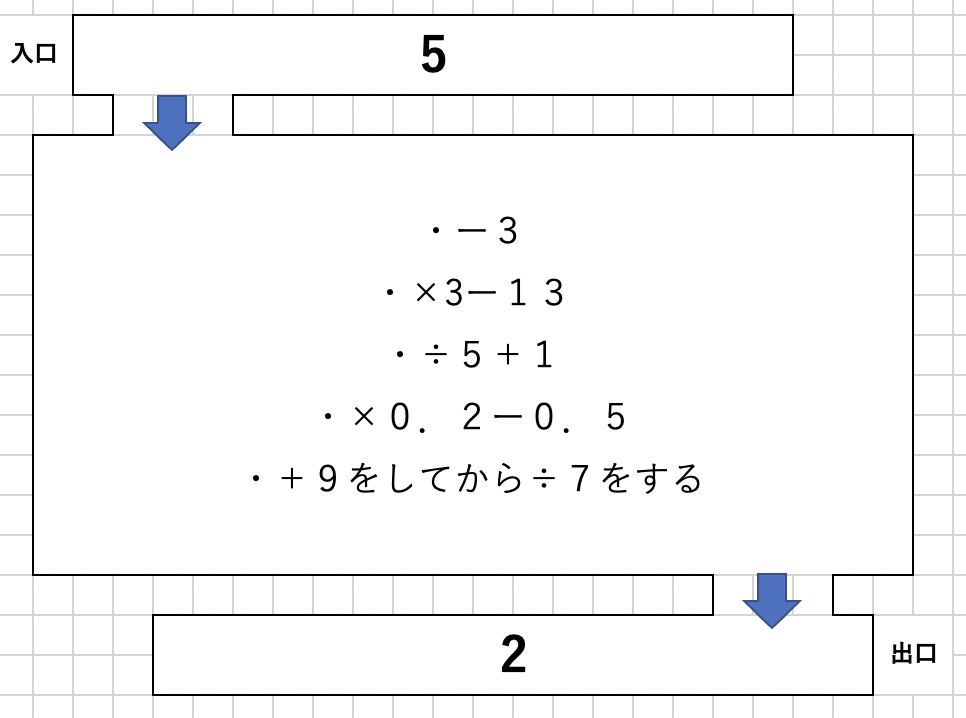
ブラックボックスを数字でやるとこうなる。
５をいれると２が出てくる。
この間で行われていることはなんだろうか？
例えば５−３、５×３−１３でもいい。
パターンは無限にある。それに今まで使った知識を総動員しないといけないので結構難しい。でも慣れてくると割とスムーズにできるようになってくる。
ぜひ子どもたちと一緒にチャレンジしてほしいなと思う。
以上！京都市中京区のアイデア数理塾 油谷がお届けいたしました！
今日の解答#093
こうやって式があっているか確かめることを検算と言います。
