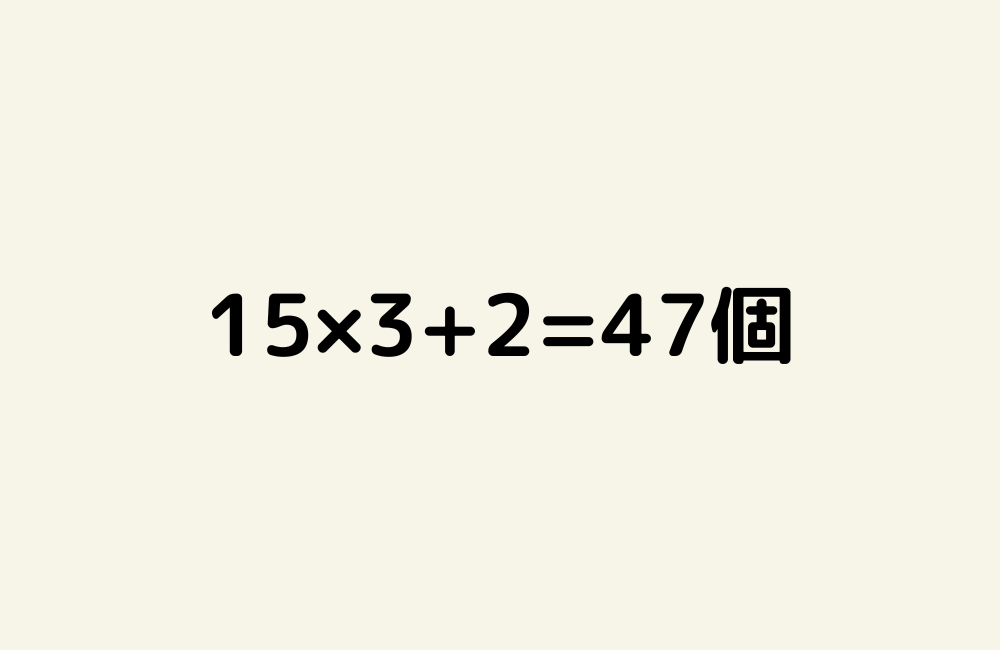数学コラムの目次
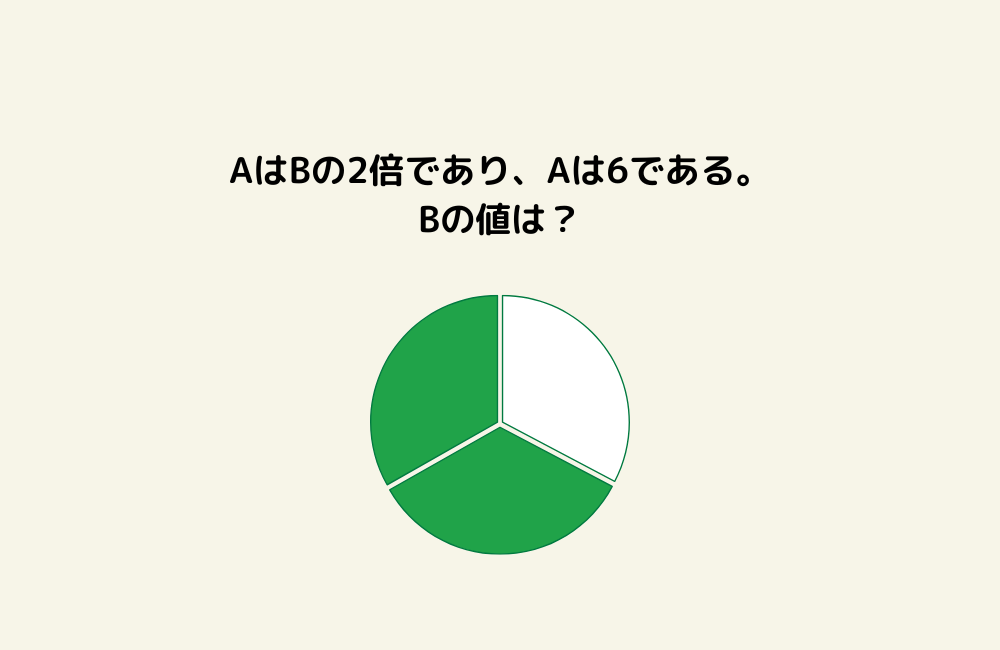
京の算数学問題#1014

アイデア数理塾はこちら
算数学コラム
こんにちは!京都市中京区でアイデア数理塾を運営しています、油谷拓哉(ゆたに たくや)です!
中学数学の最初に登場する「素数」という概念。
実はとても奥深く、数学の世界では長年研究されてきたテーマでもあります。
今日は、素数の基本と“なぜ1は素数ではないのか”という意外な事実について、わかりやすくお伝えしていきます。
素数ってなんだろう?
まずは定義から見ていきましょう。
素数とは、「1と自分自身以外では割り切れない自然数」のこと。
たとえば、
2 → 1と2でしか割れない
3 → 1と3でしか割れない
5 → 1と5でしか割れない
つまり、割れる数(約数)が2つしかない数を「素数」と呼びます。
素数の歴史 〜誰が最初に考えたの?〜
素数に関する最古の記録は、紀元前3世紀ごろの古代ギリシャにさかのぼります。
偉大な数学者ユークリッドが著書『原論(エレメンツ)』の中で、
「素数は無限に存在する」
ということを初めて証明したのです。
なんと2000年以上前から、素数は数学者たちの興味の的だったのですね!
小学生でもできる!素数の見つけ方
素数は、中学生だけでなく小学生でも楽しく探すことができます。
その方法がこちら!
◆ エラトステネスのふるい
古代の数学者「エラトステネス」が考案した、素数を見つける方法です。
やり方はとてもシンプル。以下の手順で行います。
ステップ①:2〜20までの数を書き出す
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
ステップ②:2を残して、2の倍数を消す
→ 残るのは
2, 3, 5, 7, 9, 11, 13, 15, 17, 19
ステップ③:3を残して、3の倍数を消す
→ 残るのは
2, 3, 5, 7, 11, 13, 17, 19
ステップ④:5や7の倍数を消す(今回は消すものがない)
ステップ⑤:残った数が素数!
最終的に残る素数は:
→ 2, 3, 5, 7, 11, 13, 17, 19
では、なぜ「1」は素数じゃないの?
ここが今回のテーマの本題です。
「1」は確かに「1と自分(=1)で割れる数」です。
でも、素数ではありません。
これは、数学の世界で大切な「一意性(いちいせい)」という考え方が関係しています。
◆ 一意性ってなに?
「ただ一つに決まっていること」を一意性といいます。
たとえば、10という数は
→ 10 = 2 × 5 と、素数の積で一通りに表せます。
ところが「1」を素数に含めてしまうと…
→ 10 = 2 × 5 × 1
→ 10 = 2 × 5 × 1 × 1
→ 10 = 2 × 5 × 1 × 1 × 1 × 1 …と、無限に1をかけ続けることができてしまいます。
これでは「ただ一つの分解」に決まらなくなってしまう!
だからこそ、「素数に1を含めてしまうと数学的に都合が悪い」のです。
素数の定義は変わることもある?
実は、時代や文化によって「1を素数とする」考え方も一部にはありました。
でも、今の数学の世界では「1は素数ではない」というのが一般的であり、
中学・高校・大学の教科書でもこの定義が採用されています。
「なぜそうなったのか?」を知ることで、数学の奥深さにも触れることができますね。
おわりに:素数を楽しもう!
素数は、シンプルな定義でありながら、とても奥深い世界を持っています。
「なぜ1は素数じゃないの?」
「どこまで素数は続いていくの?」
そんな疑問から、数学の探求がスタートするかもしれません。
素数の世界、ぜひお子さんと一緒に楽しんでみてください!
以上、京都市中京区のアイデア数理塾、油谷拓哉(ゆたに たくや)がお届けしました!
算数好き、あつまれ〜!
京の算数学 解答#1014