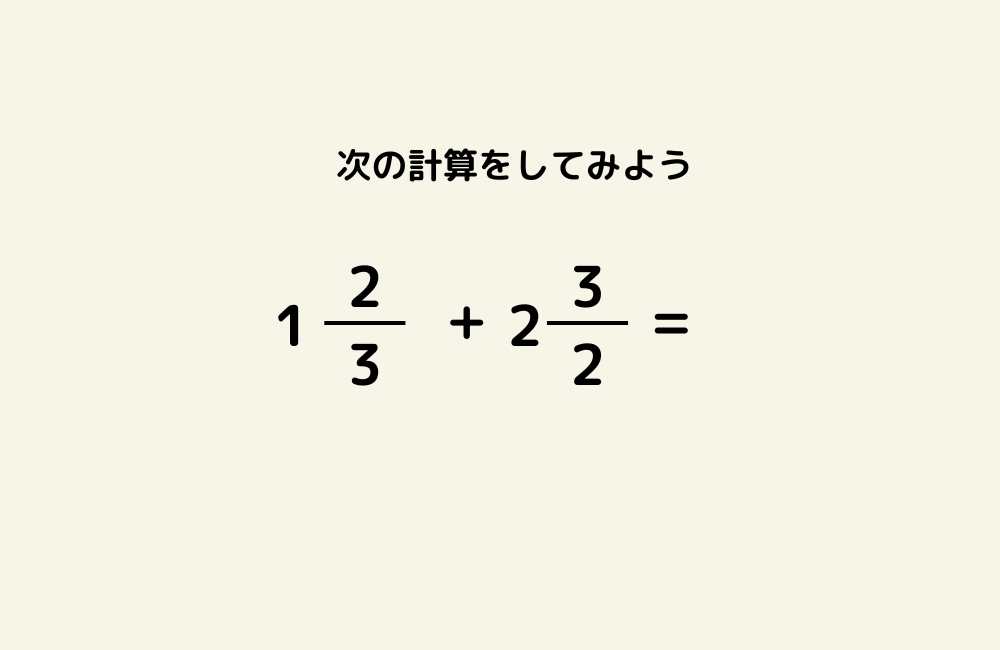京の算数学問題#1008

アイデア数理塾はこちら
算数学コラム
小学5年生の算数は、これまでの学習を土台にしながら「より高度な概念」や「複雑な計算」が登場する学年です。
「倍数・約数」「分数の計算」「単位量あたり」「割合」「速さ」「円周」など、今後の算数学習の基礎となる単元が一気に学習範囲に入ります。
この時期につまずいてしまうと、その後の学習が難しくなるため、 「どこでつまずくのか」「どう指導すれば理解できるのか」 をしっかり把握することが重要です。
そこで、本記事では 小学5年生がつまずきやすいポイントと、その克服法(具体的な指導法) を詳しく解説していきます。
1. 倍数と約数|用語の混乱を防ぐ教え方
つまずきやすいポイント
- 「倍数」と「約数」の区別がつかない
- 最小公倍数・最大公約数の求め方がわからない
- 約数をすべて書き出せない(抜けがある)
効果的な指導法
1. 倍数と約数のイメージを明確にする
「倍数」は 数をどんどん増やしていく、「約数」は その数を割り切れる数 という違いを明確にすることが大切です。
- 倍数 ⇒ 数が大きくなる(3の倍数:3, 6, 9, 12…)
- 約数 ⇒ 数を小さく割る(12の約数:1, 2, 3, 4, 6, 12)
2. 約数の書き出し方をペアで考えさせる
12の約数を例にすると、
「1×12」「2×6」「3×4」 という かけ算のペア で考えると見落としが減ります。
3. 最小公倍数・最大公約数の求め方を整理
- 最小公倍数 ⇒ 「倍数を書き出して最小の共通のものを探す」
- 最大公約数 ⇒ 「約数を書き出して最大の共通のものを探す」
➡ 練習問題:「6と8の最小公倍数、最大公約数を求めよう」
➡ 詳しくはこちらの記事で解説!
2. 分数の計算(異分母・通分・約分)|計算をスムーズにする方法
つまずきやすいポイント
- 通分を間違える(最小公倍数を間違える)
- 約分の見落としが多い
- 帯分数と仮分数の変換が苦手
効果的な指導法
1. 通分のコツを教える(最小公倍数をすぐに求める)
例:「3/4 + 2/5」を計算するとき、
4と5の最小公倍数20を見つけて通分し、分子も同じ数をかける と理解させる。
2. 約分の見落としを防ぐため、共通因数を見つける習慣をつける
- 12/18 ⇒ 「12と18の最大公約数は6」だから、「分母と分子を6で割る」
3. 帯分数・仮分数の変換を何度も繰り返す
- 仮分数→帯分数:「17/5 = 3あまり2 → 3 2/5」
- 帯分数→仮分数:「3 2/5 = (3×5+2)/5 = 17/5」
➡ 練習問題:「5/8 + 3/6 を計算しよう」
➡ 詳しくはこちらの記事で解説!
3. 小数×小数・小数÷小数|小数点の位置を意識する
つまずきやすいポイント
- 小数のかけ算・わり算を「小数点の移動」としか考えていない
- 計算ルールを覚えても、計算の意味が理解できていない
- 整数の計算と混同してしまう
効果的な指導法
1. かけ算・わり算の意味を再確認する
- 「小数のかけ算 → 倍になる」ことを意識する
- 例:1.2 × 3 → 1.2を「3倍」にする
- 「小数のわり算 → 割合を考える」ことを意識する
- 例:3.6 ÷ 1.2 → 「3.6は1.2の何倍か?」
2. 小数の計算を「整数の計算」と比較して考える
例:
1.2 × 0.3 は 12 × 3 を計算し、答えに小数点を入れる
3.6 ÷ 1.2 は 36 ÷ 12 を計算し、小数点の位置を調整する
3. 「1より小さい数」の計算で、数の変化を実感させる
- 「0.5 × 0.5」はどうなる?(1より小さくなる)
- 「0.5 ÷ 0.5」はどうなる?(1になる)
➡ 詳しくはこちらの記事で解説!
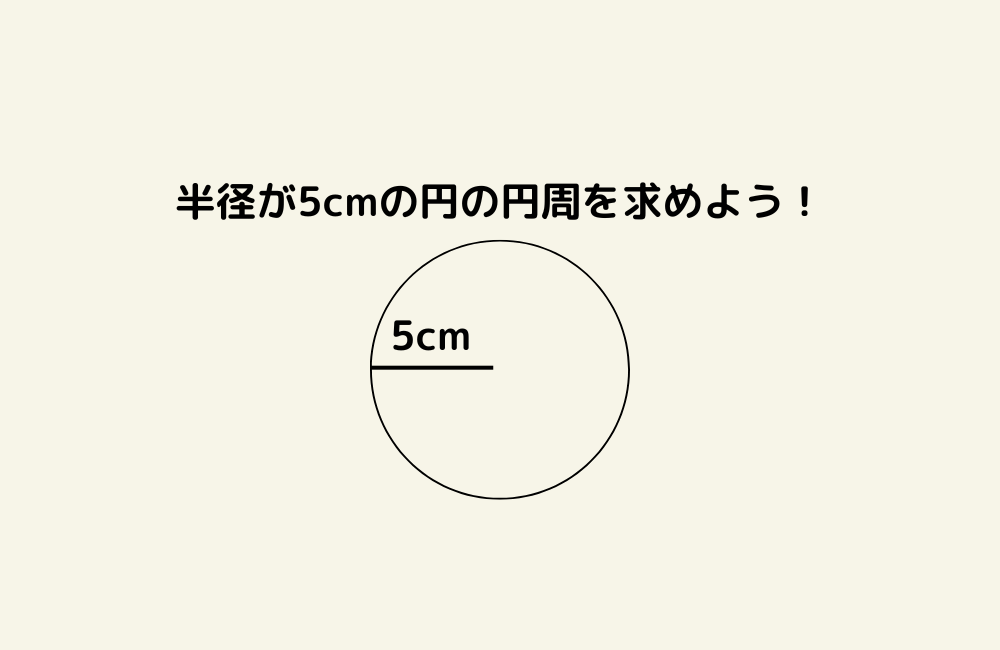
4. 多角形と円周の求め方|円周率の意味を理解する
つまずきやすいポイント
- 「円周率 = 3.14」と覚えるだけで、意味を理解していない
- おうぎ形の周りの長さが求められない
- 多角形の特性について理解していない
→内角がどこかわからない
効果的な指導法
1. 円周率の意味を説明する
- 円周率 = 直径に対する円周の比率
- 実際に 円の直径と円周を測って、3.14倍になることを確認する
2. 円周の求め方と面積の求め方を区別する
円周 = 直径 × 円周率(長さ)
円の面積 = 半径 × 半径 × 円周率(広さ)
→円の面積は詳しくは6年生で学ぶためここは触れるだけにしておく
3. 多角形の内角の求め方を2通りマスターしよう
多角形では内角の和を求める問題が頻出です。
「内角の1つの角」と「中心角を何等分?」の問題は混同しやすいので注意。
➡ 詳しくはこちらの記事で解説!
5. 面積・体積の単位変換|公式と単位を連動させる
つまずきやすいポイント
- cm²(平方センチメートル)と cm³(立方センチメートル)の違いがわからない
- 単位の変換が難しい(m² → cm² など)
- 表面積の求め方がわからない(展開図が苦手)
効果的な指導法
1. 単位の意味を整理する
面積の単位(cm²)= cm × cm(2回かける)
体積の単位(cm³)= cm × cm × cm(3回かける)
2. 単位変換の法則を理解させる
例:
1m² = 100cm × 100cm = 10,000cm²
1m³ = 100cm × 100cm × 100cm = 1,000,000cm³
3. 展開図を使って表面積を求める練習をする
- 実際に紙を切って、立体を作ることで理解が深まる
➡ 詳しくはこちらの記事で解説!
6. 単位量あたり|「1あたりの量」の考え方を身につける
つまずきやすいポイント
- 「〇〇を1とすると」の意味がわからない
- 割る数と割られる数を混同する
- 割合・速さ・比の利用につながる概念なので、つまずくと後々苦労する
効果的な指導法
1. 「1あたりの量」の考え方を練習する
例:
1m²あたりの人口 → 人口 ÷ 面積
1個あたりの値段 → 合計金額 ÷ 個数
2. 割る数と割られる数を意識させる
「どちらを1とするのか?」を常に確認しながら計算させる。
➡ 詳しくはこちらの記事で解説!
7. 速さ|単位変換をスムーズにする方法
つまずきやすいポイント
- 速さ・時間・距離の関係を混乱する
- 時速→分速→秒速の変換ができない
- 問題文の単位を読み間違える(kmなのにmで計算)
効果的な指導法
1. 「速さの三角形」を活用する
速さ・時間・距離の関係を
- 速さ = 距離 ÷ 時間
- 距離 = 速さ × 時間
- 時間 = 距離 ÷ 速さ
の 三角形の図 で視覚的に教える。
2. 単位変換の基本を徹底
- 1時間=60分
- 1分=60秒
- 1km=1000m
➡ 詳しくはこちらの記事で解説!
8. 割合|もとにする量を見つける方法
つまずきやすいポイント
- 「もとにする量」を勘違いする
- 百分率・歩合の変換がわからない
- 文章題の情報整理が苦手
効果的な指導法
1. 割合の基本公式を整理
- 割合 = くらべる量 ÷ もとにする量
- 例:「あるクラスの40人のうち、男子が16人。このクラスの男子の割合は?」
→ 16 ÷ 40 = 0.4(40%)
2. 「もとにする量」を見極める練習をする
文章題では、「何を1とするのか?」 に注目して情報を整理する。
➡ 詳しくはこちらの記事で解説!
まとめ|小学5年生の算数を克服するポイント
用語の違いを明確に(倍数・約数、速さの単位など)
計算ルールを確実にする(通分・約分・割合の公式など)
文章題は情報を整理しながら解く(もとにする量を明確に)
小学5年生の算数をしっかり理解することで、6年生以降の学習がスムーズになります!
京の算数学 解答#1008