数学コラムの目次
京の算数学問題#717

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
期末テストが近づいてきましたね!
中学3年生は今の時期平方根をやっていると思います。
今日は平方根の解き方のコツをお伝えしていきます。テスト前の参考にしてくださいね〜!
平方根ってなに?
平方根とは、「2乗するとある数aになる数」を言います。
例えば4の平方根とは言い変えれば「2乗して4になる数は?」と聞かれているので、±2です。
同様に5の平方根は?とは「2乗して5になる数は?」と聞かれているので±√5となります。
平方根と√(ルート)の違い
平方根は上述の通りですが、一方で√(ルート)は+と−のどちらかの数を指すものです。
上記の問題を例に考えてみましょう。
4の平方根は?と聞かれた場合は±2ですが、
√4=2となります。
一方で−√4=−2となります。
同様に5の平方根は±√5であり、√5はこれ以上計算できないのです。
ここはよく間違えるポイントなので注意をしておきましょう!
√の大きさを感覚的に掴む
例えば
1の二乗は1
2の二乗は4
3の二乗は9
4の二乗は16ですよね。
つまり言い換えれば
1は1を二乗した数である。
4は2を二乗した数である。
9は3を二乗した数である
となります。
ここでポイントとなるのは1→4→9→16→25とどんどん差が大きくなっていますよね。
例えばこの1と4の間にある数があってもいいと思いませんか?
そこで登場したのがルートです。
例えば√3であれば「二乗したら3になる数」なので、1〜4の間にあるはずです。
つまり√3は1.〜という整数部分を持つという事がわかります。
このようにおおよその値を推定するのもとても重要な考え方です。
√の計算は文字式で考えよう!
例えば次の計算をしてみましょう。
√2+√3+2√2−2√3
ここで√2=x、√3=yとおきます。
X+y+2x-2y=3x-yとなります。
つまり答えは3√2−√3となります。
ルートの計算は視覚的にわかりづらくルートの中に数字があるのでついついルートの中の数字同士を足してしまったりします。
視覚的に慣れるまでは一旦文字においてみると計算法則がわかりやすくなりますよ。
ルートの計算の手順
ルートの計算も下記の順序に従えば大丈夫です!
①○乗がある場合は展開する
②a√bの形に直し、分数は有理化しておく
③÷を×になおす
④()を外す
⑤同類項をまとめる
⑥分数の場合は有理化をし、約分を確認する。
問題を解いてみましょう!
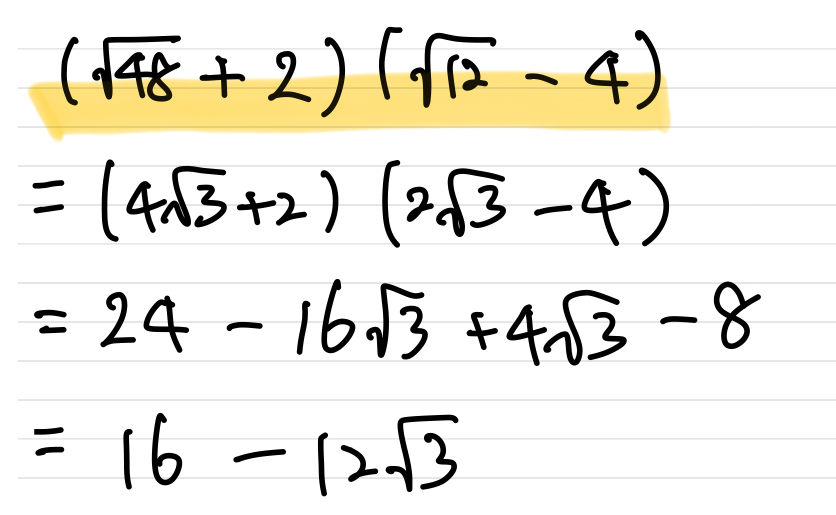
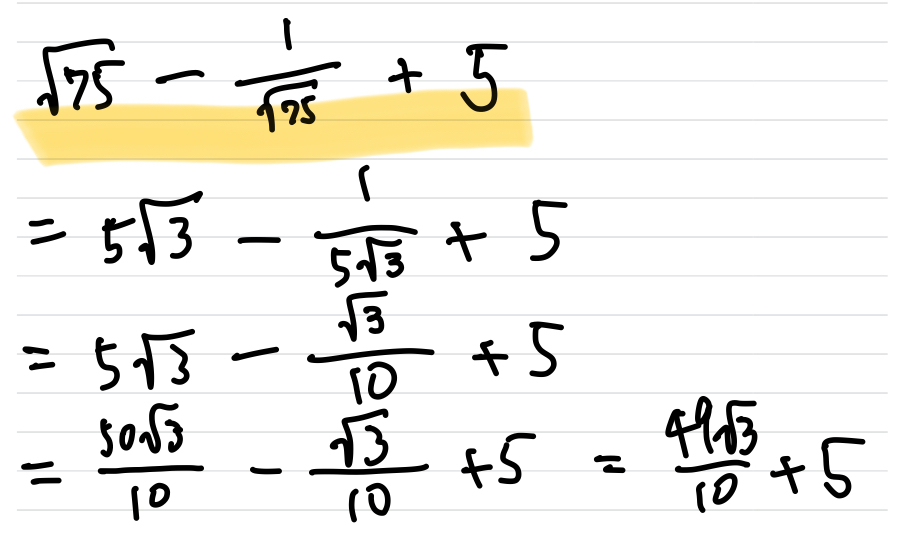
このように計算の順序を明確にしておくと計算ミスも減ります。
初めは途中式を丁寧に書く事が面倒くさいと感じられるかもしれませんが、途中式は計算スピードを上げるための練習なのでしっかり書く癖をつけておきましょう!
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#717




