数学コラムの目次
京の算数学問題#611

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
つい先日からSNSでおバズり申し上げているのが「ねじれの位置」でした。
京都大学や大阪大学の入学試験の問題でも取り上げられ受験生たちも「ノーマークだった」と話題になっていたねじれの位置ですが定義自体は小学生でもわかるようなものなのです。
今日は今話題のねじれの位置について解説をしていきます!
ねじれの位置ってそもそもなに??
ねじれの位置とは「平行ではなく交わらない2つの直線の位置関係」のことです。
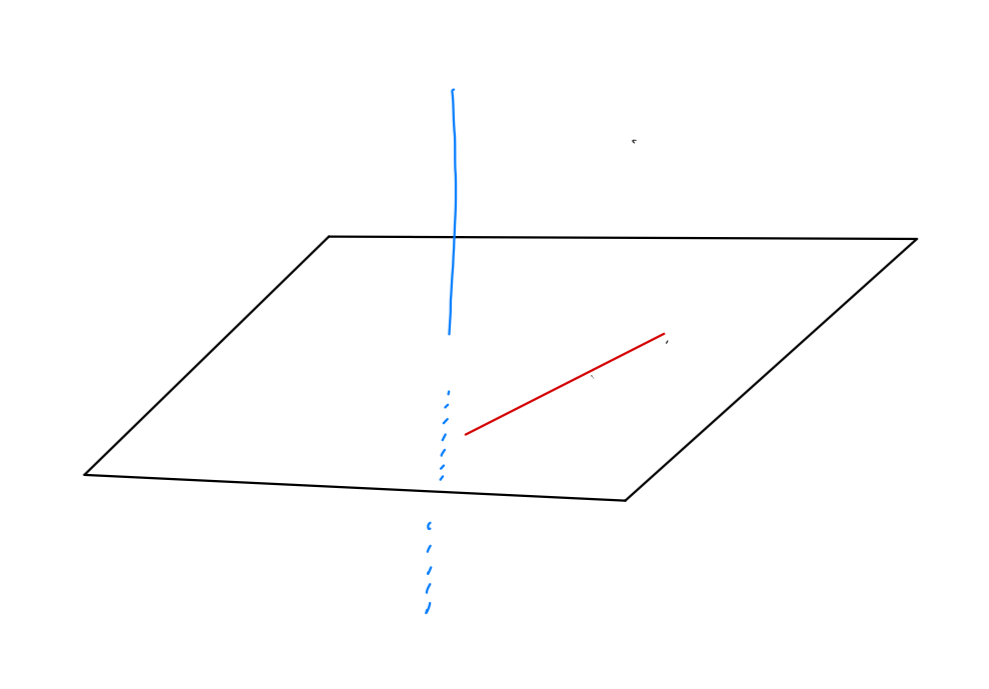
この図の2本の線は平行でもありませんし交わる事もありませんよね。
これがねじれの位置という関係です。
直方体で考える場合。
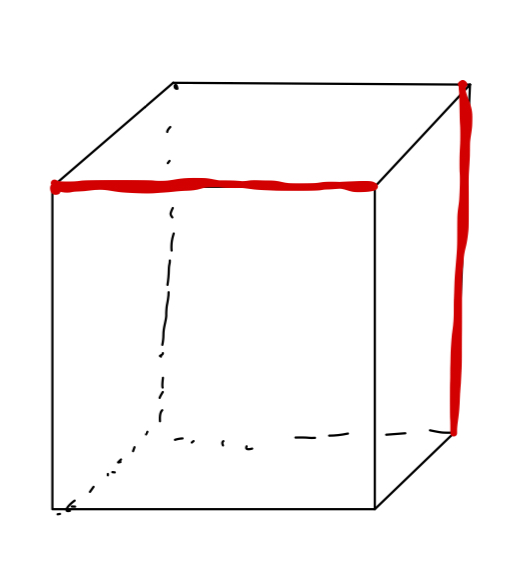
この位置がねじれの位置となります。
実は身近にあるねじれの位置
実はねじれの位置という関係性は身近なところにたくさんあるのです。
例えば立体交差点や地下道なんかはまさに平行でもなく垂直でもないねじれの位置にあります。
平面でなく空間を利用することで渋滞の緩和やデザイン性の向上などさまざまな利点があります。
大阪大学2024で出題されたねじれの位置の問題
「空間内の2直線l,mはねじれの位置にあるとする。lとmに直行する直線がただ1つ存在する事を示せ」
この問題はSNSでバズっていた今年の阪大の前期入試の問題。
ねじれの位置自体は中学1年の空間図形の単元で学びますが、あまりマークされていない単元であった事が今回のバズりにつながったそうです。
今回の問題のポイントは無数にあるねじれの位置の直線のうち1つl を決めることにある。
いわゆる盲点をつかれた!という問題である。
解いていると面白いな〜と思うものの、フルスロットルで授業を終えた油谷の体力がつきそうなので今日はこの辺で笑
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#611




