数学コラムの目次
京の算数学問題#341

アイデア数理塾はこちら
算数学ブログ
中学に入ると学ぶ指数ですが、高校2年の指数関数にてより深く学ぶことになります。
例えば3の2乗は9となります。
これは3×3という意味だからです。
では0乗ってどうなるのでしょう?また、0の0乗はどうなるのでしょうか?
今日のブログでわかりやすく解説していきます!
(仮説)0の0乗は0じゃないの?!
そもそも指数とは、何度同じ数をかけているか?と習っていたはずです。
例えば4の3乗(以下指数を4^3と書きます)の場合、4×4×4=64という意味になり、4が3回かけてあるという解釈になりますよね。
じゃあ4^0はどうでしょうか?4が0回かけてあるので0と言えるのか?!
実は数学の定義においてこれを0にすると非常にめんどくさいことになります。
0乗は1になる証明
指数の定義で
こんなのがありました。

n=0のときこの等式が成り立つとするなら、
a^0は1でないとスムーズに計算ができず都合が悪いという事がわかります。
ですので指数関数で学ぶ0乗は1とみなすのです。
0の0乗は1になる!ただし、、、
高校数学で学ぶ範囲の中では下記のように1と学んでいきます。
ここでa×2=2aとなるように、a=1×aと表す事ができます。
つまり、a^0とは掛け算下記のように表せるので、0の0乗も1とした方が都合が良くなります。

ただし!これはあくまで都合がいいので1としましょうと定義をした上での話です。
代数学など別の視点では、
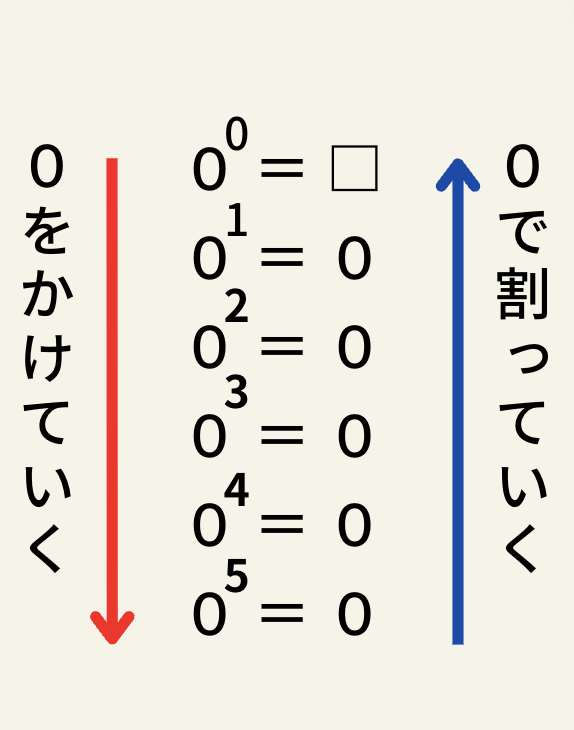
この画像のように、0を順にかけていくと指数が増えていくのですが、0で割ると指数は減っていきます。
ただ0乗の場合0で割るという行為自体ができないので定義できないとされています。
数学の公式は特に理由のないものもある
このように数学の公式は一見意味がありそうで説明できそうだけれどもそうした方が都合がいいからそうしましょうと言った「ちからわざ」が結構あるのです。
このような視点で数学を考えてみるのも面白いですよね^^
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#341




