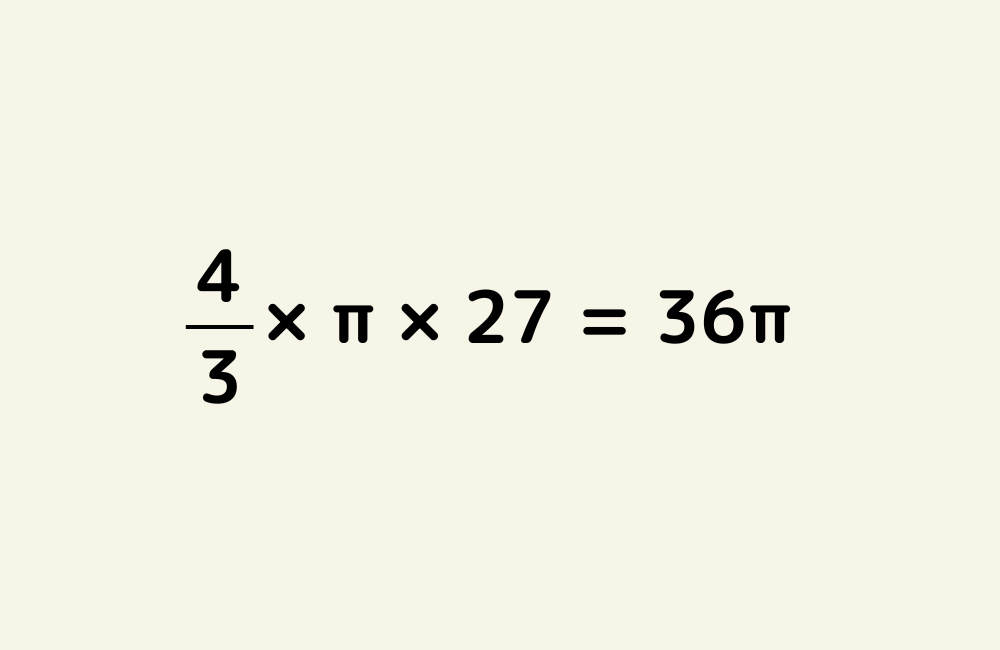数学コラムの目次
京の算数学問題#295

アイデア数理塾はこちら
算数学コラム
特に小学生において年々問題が難しくなっているように感じる^^;
図形問題はいかにイメージできるか?が鍵になるのですが、機械的にも解けてしまうのが小学生です。
今日はおうぎ形を例にどんなふうに解くのか?を書いていますので、解くのに迷ったら是非みてください^^
円の面積の求め方
公式:半径×半径×3.14(円周率)
これは比較的覚えやすいと思います。
円周の求め方と混同しないようにさえすれば大丈夫ですが、そもそもなぜこの式で面積が求められるのでしょうか?
おそらく小学生にとって面積とは、正方形をイメージする場合が多いと思います。
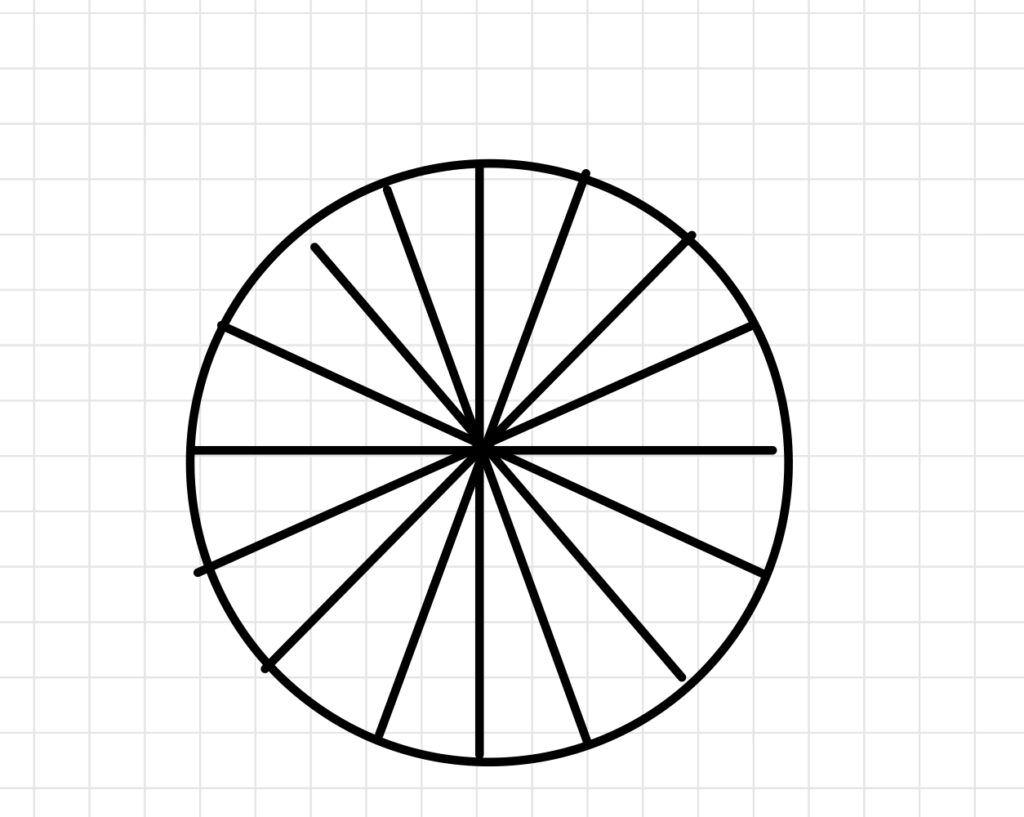
円をめちゃくちゃ細かく分けていき並べると。
細かく分ければ分けるほど長方形に近づいてきます。
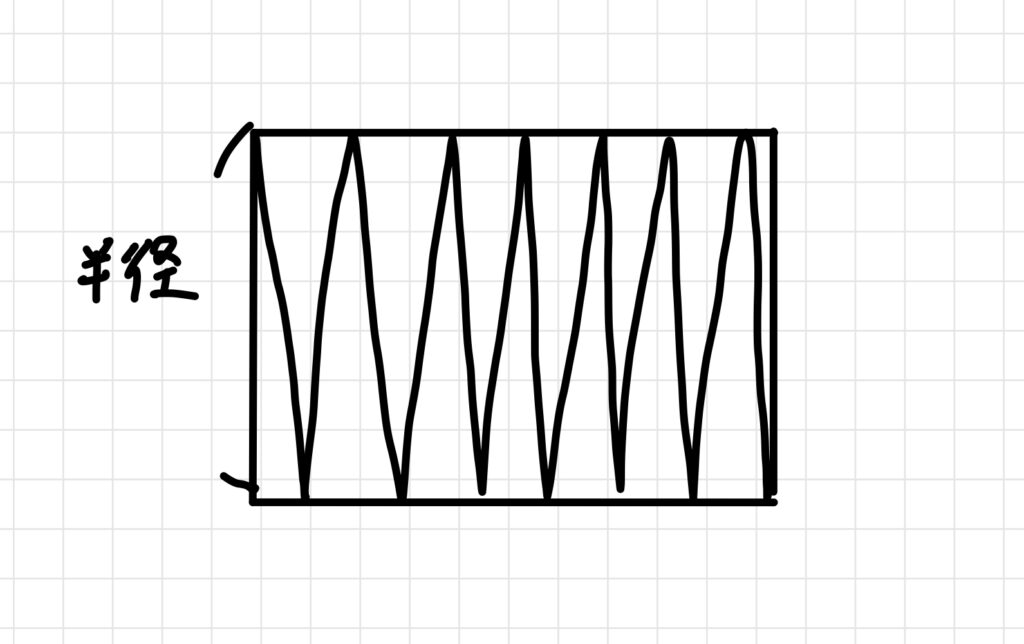
縦は半径の長さで、
横は円周の長さの半分ですので、円周÷2の長さになります。
また、円周は直径×3.14ですので直径は半径の2倍です。
つまり長方形の面積はたて×横で求められるので、
半径×円周÷2=半径×半径×3.14となります。
ただ、円は丸なので、いくら細かく切って繋いでも弧の部分はどうなるの?と疑問に思われる方もいらっしゃると思います。
ですが、数学には限りなく0に近い場合0として扱うと言う考え方もあり、そこら辺は気にしなくて大丈夫です。
あくまでも円を限りなく細かく分けた時と言う解釈になります。
円周率ってそもそも何?
円周率は円周の長さは円の直径の何倍か?を表した数字です。
つまり、円周率=円周の長さ÷円の直径の長さで求めることができます。
さまざまな円の円周と直径の関係性を調べたところ3.14159265….と割り切れない数字ですが、一定になることがわかりました。
それゆえ直径から円周の長さを推定できるようになったのです。
おうぎ形の面積の求め方
おうぎ形は円の何%か?と言うのが基本的な解釈になります。
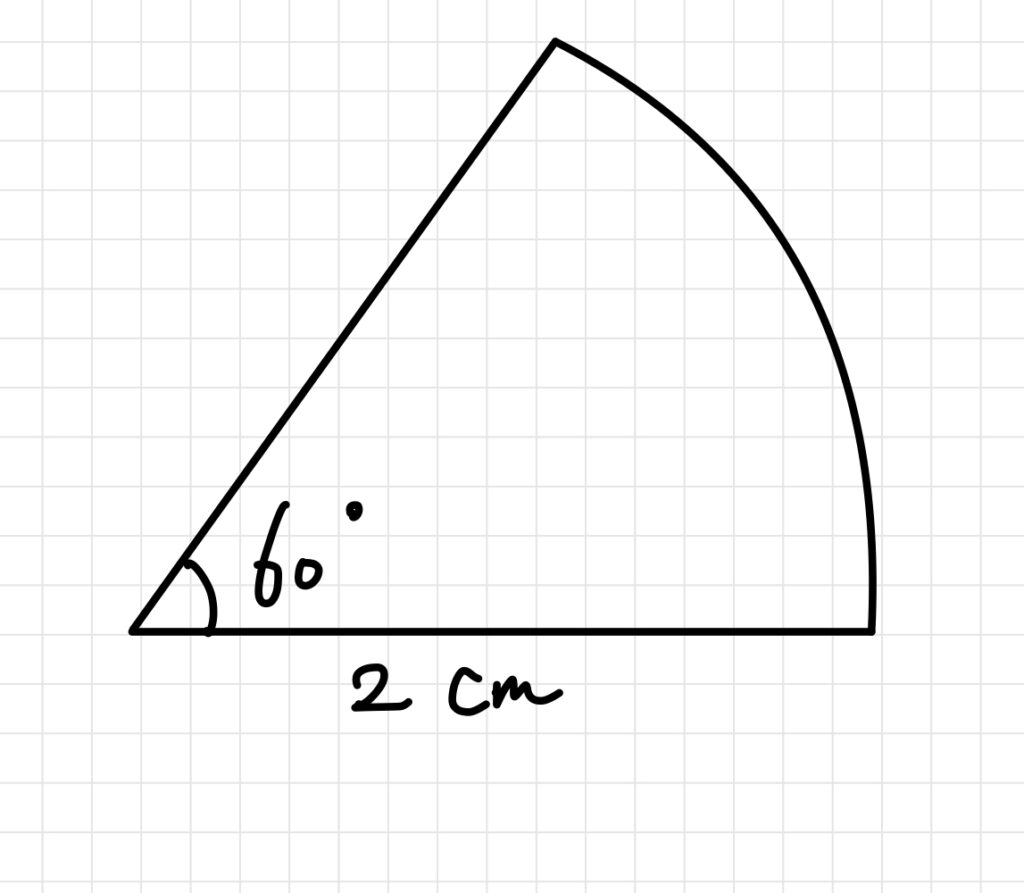
例えば上記の図ですと、
円の場合、2×2×3.14=12.56となりますが、
この場合中心角は60度ですので、円の中心角360度に対して
60/360になっていることがわかります。
つまり、12.56×60/360≒2.1となります。
おうぎ形のポイントは本来360度ある円が中心角何度までしか無いか?を割合で求めることです。
レンズ型のおうぎ形
おうぎ形の頻出問題でレンズ型と言うものがあります。
通常の解き方は対角線を引き、おうぎ形の面積から二等辺三角形の面積を引き、2倍します。
この場合だと
(おうぎ形の面積)3×3×3.14×90/360=7.065
(二等辺三角形の面積)3×3×1/2=4.5
(7.065-4.5)×2=5.13
でも実はこの問題は、一発で解けちゃいます!
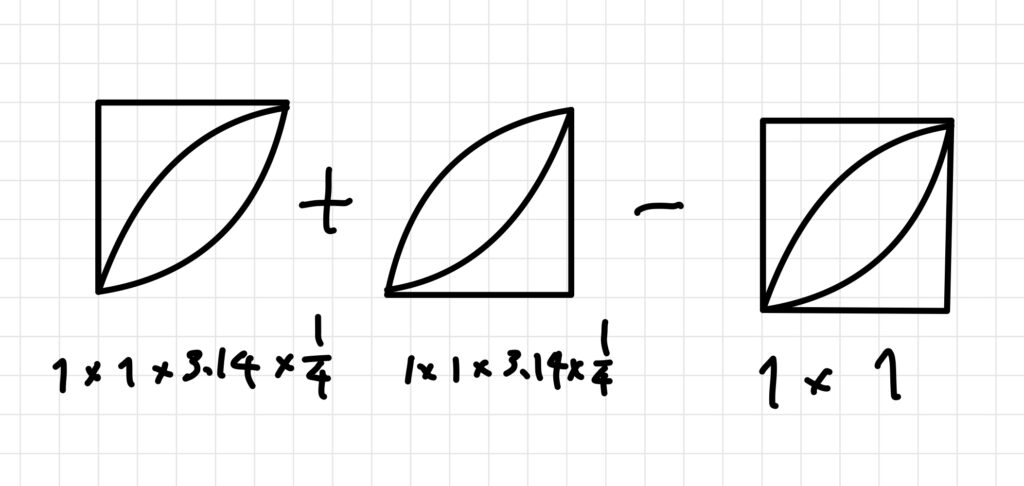
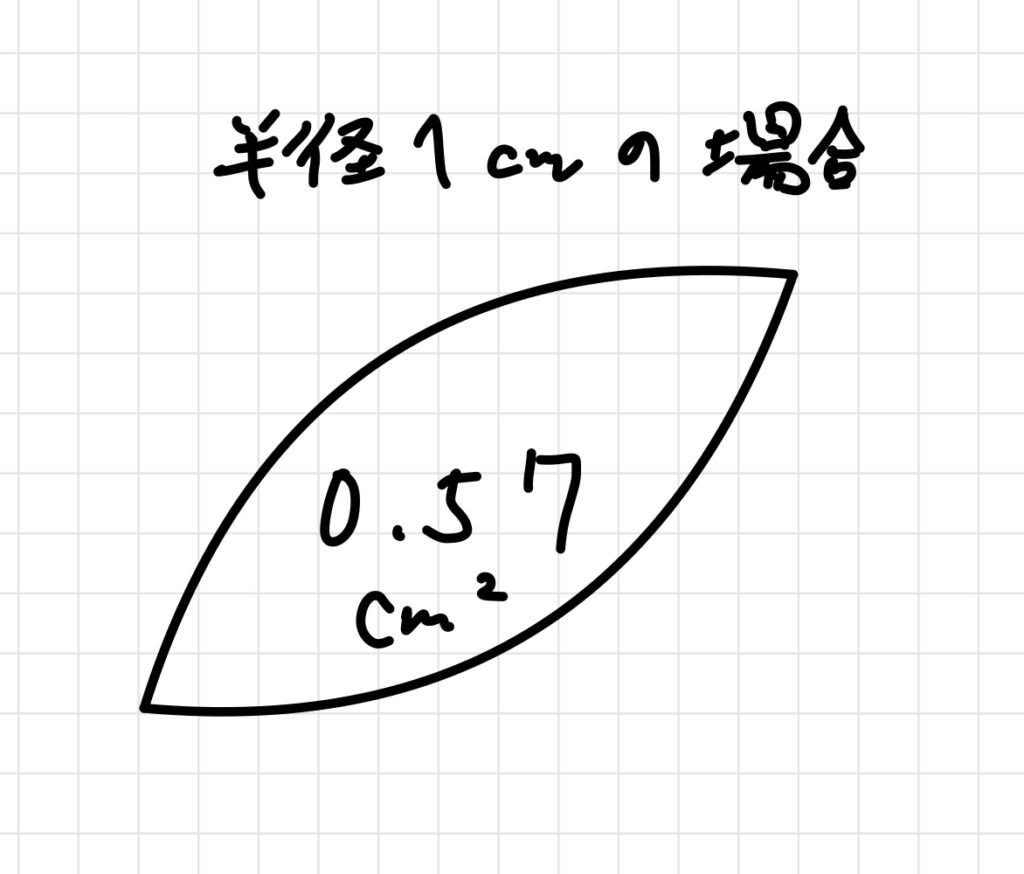
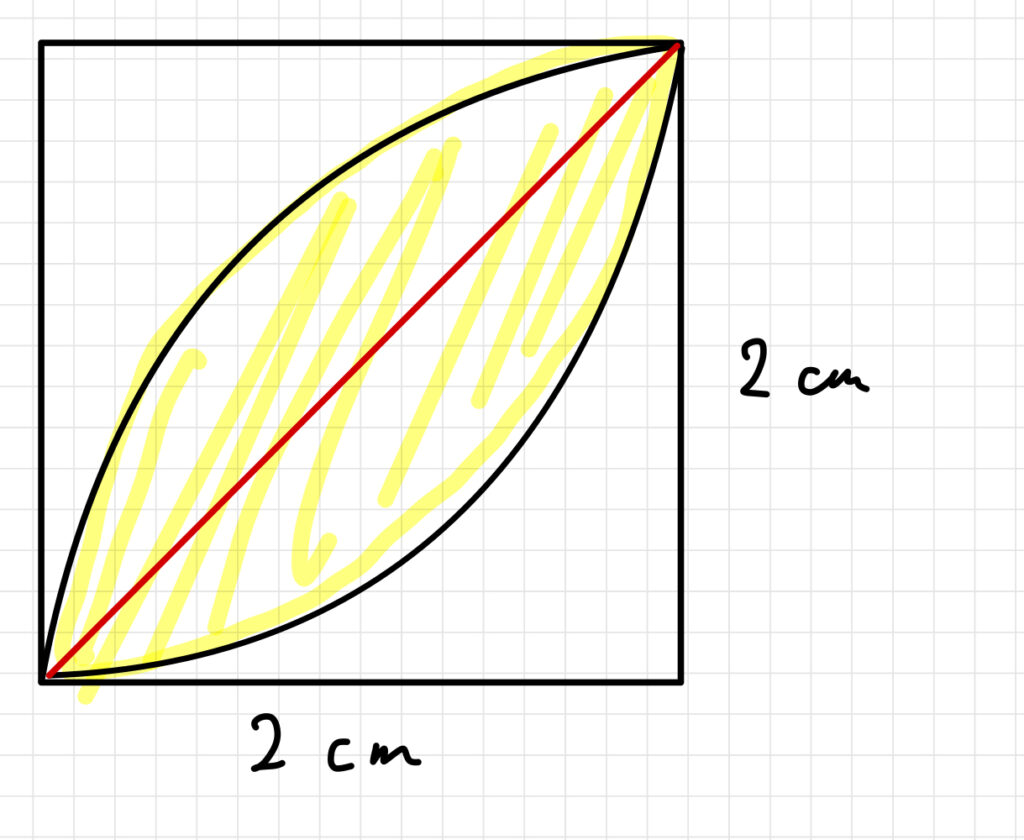
半径1のおうぎ型を考えた時に、
中央のレンズ型を求めようと思うと、このように0.57という数字が出てきます。
つまり、半径3のおうぎ形の場合は3×3×0.57で答えが出せることになります。
不思議ですね〜
でも公式ってこうやってできてきたんだと思うとやっぱ数学って面白いですね^^
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
京の算数学解答#295