数学コラムの目次
今日の数学問題

今日の数学コラム
夏休みを目前に期末テストの結果がそろそろ帰ってきて成績表の結果にドキドキしているのではないでしょうか?中学生になるとテストの様式が一気に変わり数学になった事で一気に難しくなりましたよね。
これから夏休みを迎え次の単元は中学2年生では連立方程式〜一次関数です。
今日は9月の中間テストでスタートダッシュを決めるために連立方程式を詳しく解説していこうと思います。これを読めばもう大丈夫^^休み明けぜひ良いスタートを切りましょう!
連立方程式とは?
2つ以上の方程式を組み合わせた物の事を言います。
では復習も兼ねてそもそも方程式とはどういう物なのか?

このようにまだわかっていない数をxとおいた等式の事を言います。
=を等号と言います。=を挟んで左側(3x+2)を左辺、5を右辺と表現します。
3x+2が5になるxを求める事を方程式を解くと言います。

方程式の解き方はx=という形にするのが基本です。
左辺から-2をする場合、右辺からも-2をする必要があります(2つ目の式)
これにより左辺の+2が右辺へ-2となり移動しているように見えます。これを移項と言います。(3つ目の式)
以下同様に両辺を÷3し、x=を求めるのが方程式の解き方です。
この方程式を連立する(並べた)のが、連立方程式です。
蛇足ですが方程式の語源は中国で用いられていた算術で格子状に数を並べて計算していた事から由来しています。
二元一次方程式とは?
中学2年生で学ぶ連立方程式は主に2元1次方程式を連立させたものを扱います。

元とは文字の種類です。この式の場合はxとyの2種類の文字が使われていますので2元となり、次は式の次数を表しますので1次式となります。
補足問題
次の式は何元何次方程式でしょうか?
(1)3x+2y+z=2
(2)x+3=1
(3)xy+2=0
答え
(1)3元1次方程式
(2)1元1次方程式
(3)2元2次方程式
連立方程式の2つの解き方
連立方程式は方程式の解き方が基本になります。
加えて2つの式を足したり引いたり(加減法)、代入したり(代入法)して、一方の文字を消し一つずつ数を紐解いていきます。
加減法の解き方
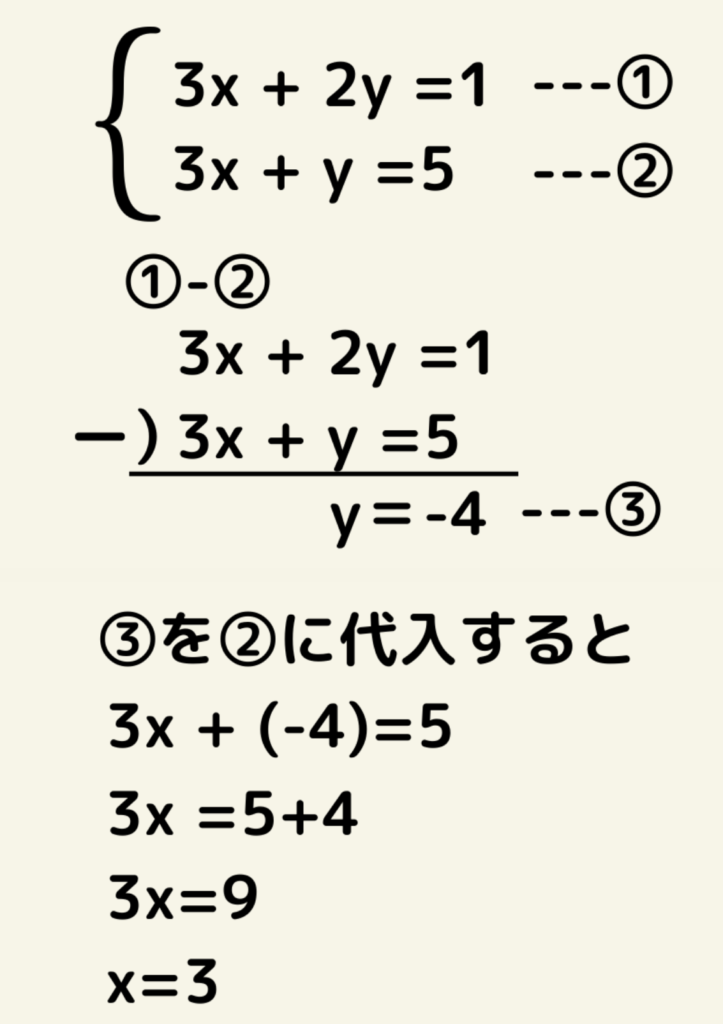
加減法は一方の式から一方の式を足したり引いたりして、文字を一方に統一し方程式にしてから求める方法です。今回の例題では、3xが揃っていますが、揃っていない場合はかけたり割ったりして係数を揃えてから加減法を使いましょう。
なぜ加減法が成り立つのか?
加減法は2つの式の共通点を抜き出すことによって、一方の文字に統一する事ができます。 例えば次のような例題があったとします
【例題】
いちご3個とりんご2個を買うと150円した。
いちご2個とりんご1個を買うと90円でした。
いちごをx円とりんごをy円とすると、
3x+2y=150
2x+y=90という2つの式が出来る。
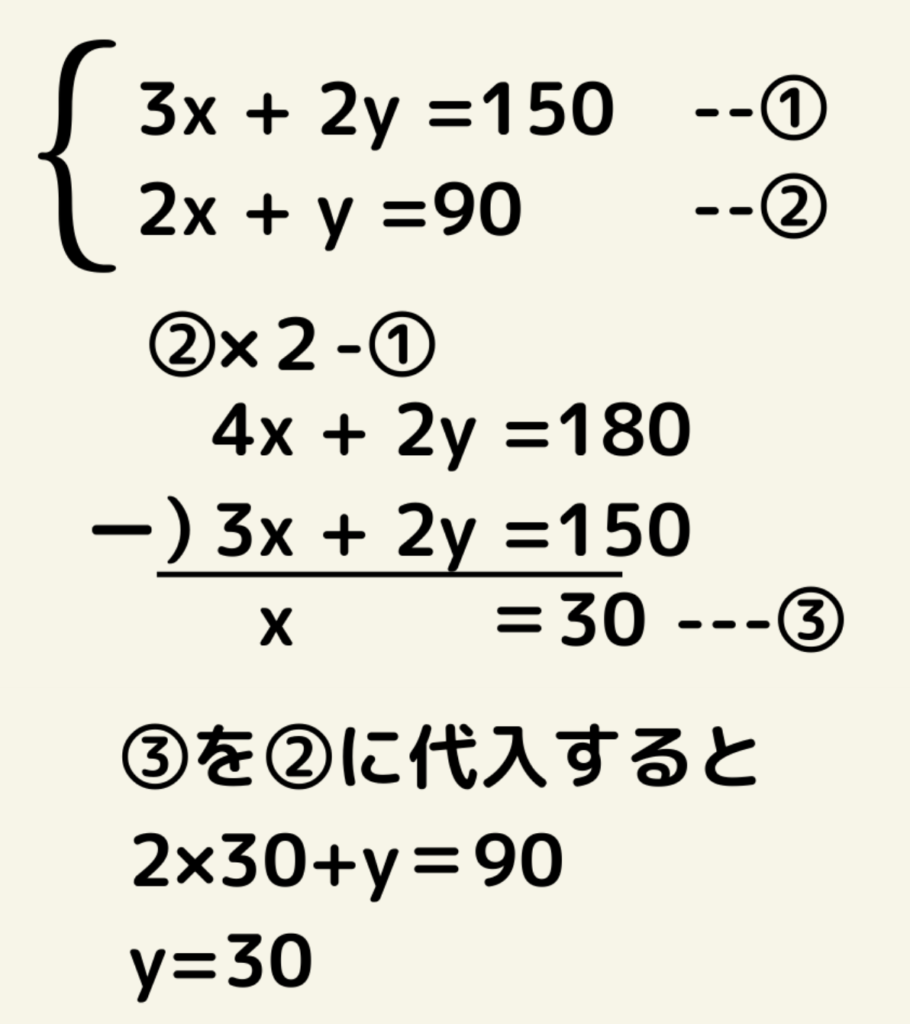
よっていちごは30円りんごは30円という答えになる。
加減法はイメージで理解すると良い
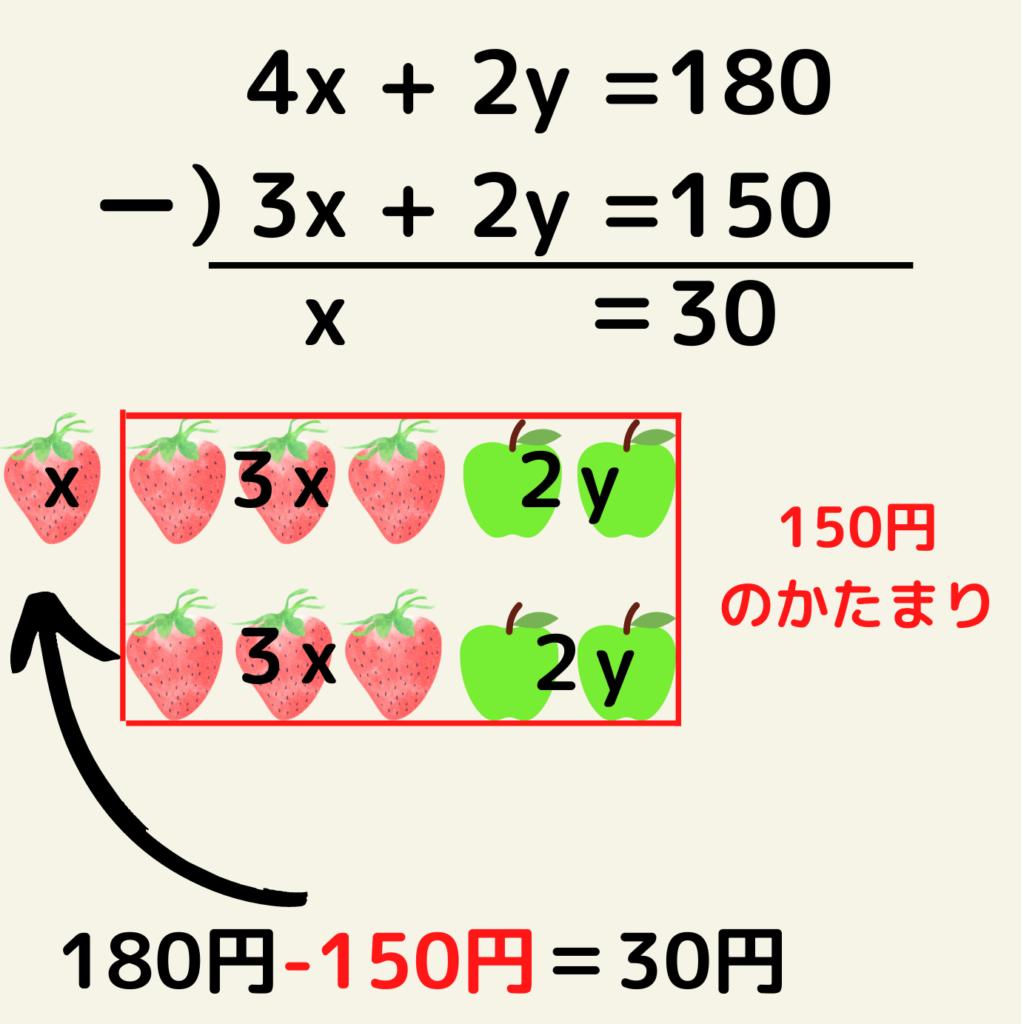
1つ目の式をこのように図で表すと、係数を揃えて上の式から下の式を引く事で係数が減るのがわかる。
イメージとして連立方程式を捉えると原理が分かりやすいですね。
代入法

代入法は一方の式をy=もしくはx=という形に整理しもう一方の式に代入する事で文字を減らす手法です。
この場合②の式を整理してy=にしてから①のyに-3x+5を代入している。
計算が少し難しいので敬遠される場合も多いが、代入法で解きなさいといった解法を指定されている問題も出されることもありますし、代入法の方が解くのが簡単な場合もあるので必ず覚えておきましょう。
補足
②を整理したときに③ではなく②’(2ダッシュと読みます)とした理由は、②の式を変形しましたよという意味を強調するためです。
③としても問題はありませんが、こだわりです笑
代入法をイメージで理解しよう

同様の問題を代入法で解くとこのようになる。
イメージとしては、

要するに代入方でも加減法でも同様で、xとyに同じ値が入ると仮定しているので足したり引いたり代入したりが出来るのです。
連立方程式の解答の書き方に気をつけよう!
- 2つの式に①,②と番号を振る(後に何の式について言っているのかを分かりやすくするため)
- 何の操作をしたのか明確に示す(加減法の場合は①―②、②+①×2など、代入法の場合は①を②に代入するなど)
- x,yどちらかが分かったら③とおく(操作を分かりやすくするため)
- ③を①か②の式に代入する。
- 解答を書く。(解答の書き方は学校によって指導が違うので学校の先生に確認しよう!)
解答の書き方は以下の場合が多い。
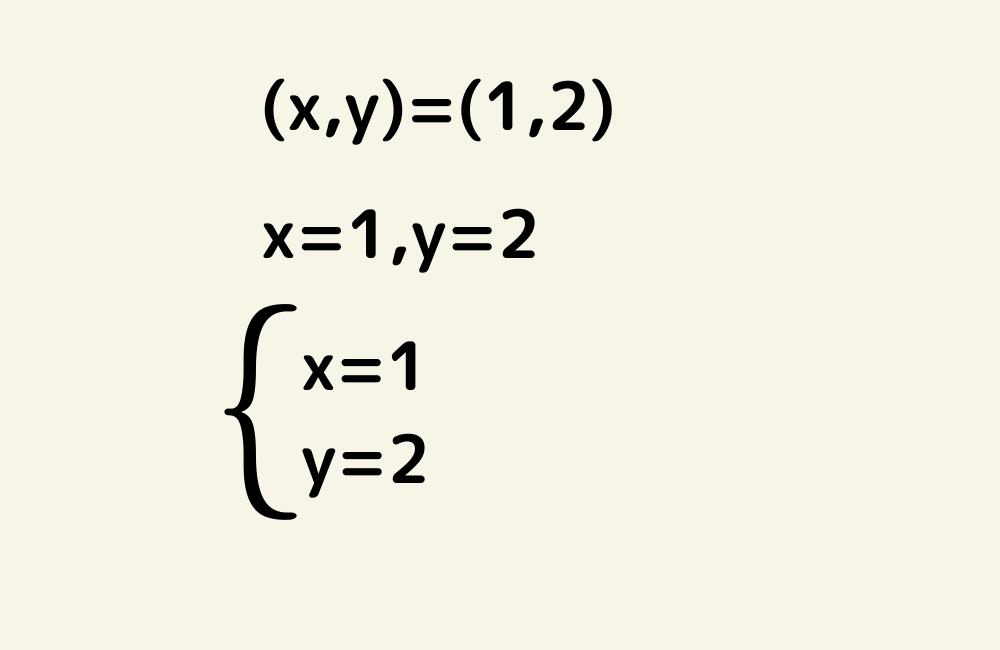
正直どれでも正解です。
解答は、出題者に自分の考えを伝えるためにあるのできちんと教科書通りに書けるようにしておきましょう!
相手に伝わる解答が書けるという事はきちんと流れを理解しているという事なので学校の先生は特に重要視して見ています!
減点されるともったいないのでここは丁寧に^^
解答が合っているかの確認方法
xとyを出す事が出来たら合っているかどうかを確認するもの必要な事です。
テスト中は全てを確認する必要はありませんが自信のない問題や、解答の確かめを繰り返していると、あれ?これおかしくない?とミスに気づく力が身に付きます。
確認方法は求めた答えを①と②の両方に代入する事です。

例えばこの式の場合解答は
x=3,y=-4と解く事ができましたので、①と②に代入してみます。
①の式に代入すると
(左辺)3×3+2×(-4)=9-8=1なので(右辺)と等しくなります。
②の式に代入すると
(左辺)3×3+(-4)=9-4=5なので(右辺)と等しくなります。
ここから求めたx,yが正しいという事がわかります。
グラフで理解する連立方程式

中学で学ぶ連立方程式はxとyの2つの文字を使います。
①と②の式のxとyを加減法、代入法を用いて共通の値を求めるのが連立方程式を解くというものでした。
①の式について
x=1の時y=0、x=2の時y=-1というように、どちらか一方の値が決まればもう一方の値が決まります。これを関数と言います。中学1年生や小学生で学んだ比例反比例のグラフと同じ理屈です。
表にすると

②の式について
同様に表にすると

この2つをグラフにすると、
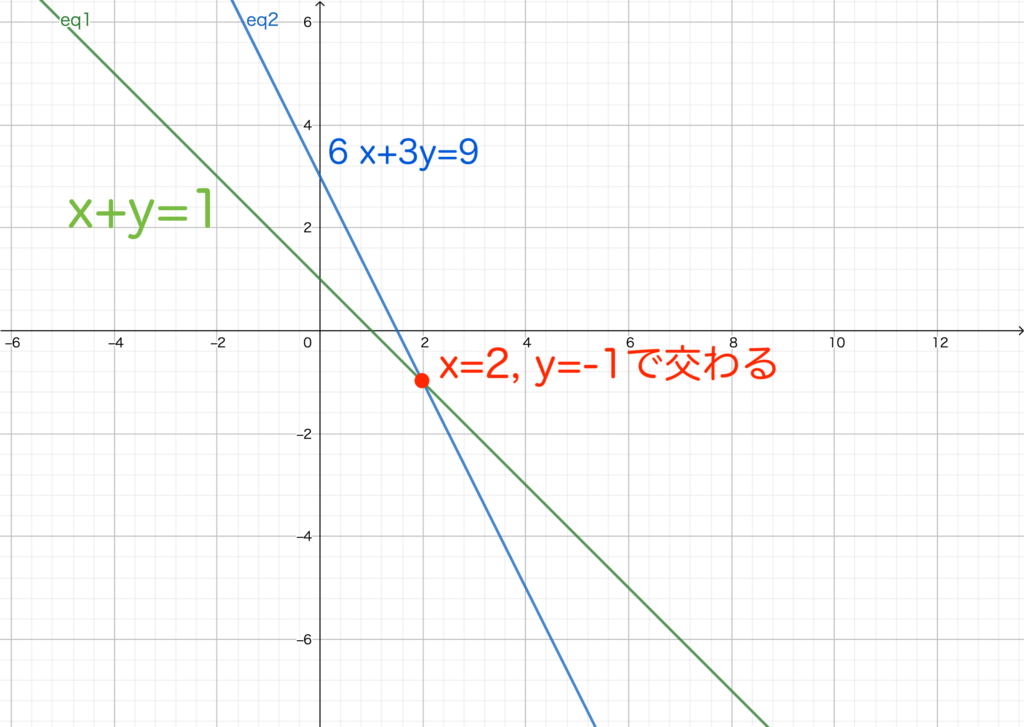
このように①と②の共通解つまり、交点が連立方程式の解だと言い換える事が出来ます。
この考え方は本質を理解するためには非常に重要で、こんなイレギュラーな問題も解凍する事ができます!
イレギュラー問題その1

この問題を加減法で考えてみましょう。
2の式全体を2で割るとx + y=1になりこれは①と同じになります。
この式を①式から引いた場合式が左辺も右辺も0になってしまいxとyどちらも消えてしまい計算する事ができません。
そんな時は①と②の交点が連立方程式の解だという事を使いましょう!

そうすると同じ直線なので全て重なってしまいます。
よってこの連立方程式の解は「全ての実数」になります。
イレギュラー問題その2

これも同様に加減法で考えると、
②の式全体を2で割るとはx+y=4となりますので、
この式を①から引いても0=−2となり、おかしな事になります。
この場合もグラフを考えると

このように並行になり交わることはありません。
つまり交点がないと言い換える事ができます。
よってこの連立方程式の解は「解なし」になります。
これで安心!連立方程式頻出問題7パターン
係数が揃っている連立方程式

このように2つの式の係数どちらか一方が揃っている場合は加減法で計算しよう!

つまり、(x,y)=(21/4,-9)が答えになります。
そのまま引けば比較的簡単に答えを出すことが出来ます。
【計算を楽にする裏技】
このような問題の場合、加減法が定石ではありますが、代入法を応用するともっと計算を楽にする事が出来ます。
例えば①の式4x+y =12 を 4x=12-y の形に変形します。
そして②の式に代入をすると
(12-y)+2y=3とすれば、y=-9 とかなりスムーズに計算することが出来ます。
x=でしか代入法は出来ない訳ではなく、少し柔軟な発想を持てばこのように簡略化ができるのが数学の面白いところですね^^
係数がバラバラの連立方程式
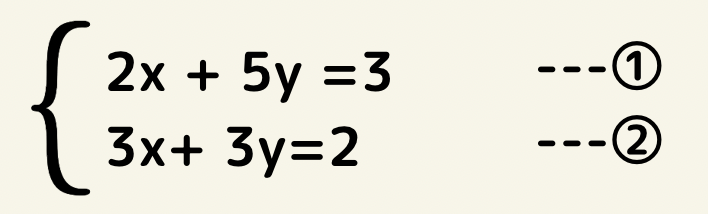
係数がバラバラの場合は①②それぞれのxかyのどちらかの係数を最小公倍数で揃えます。
今回の問題では2xと3xに着目し、①×3ー②×2で計算していきます。
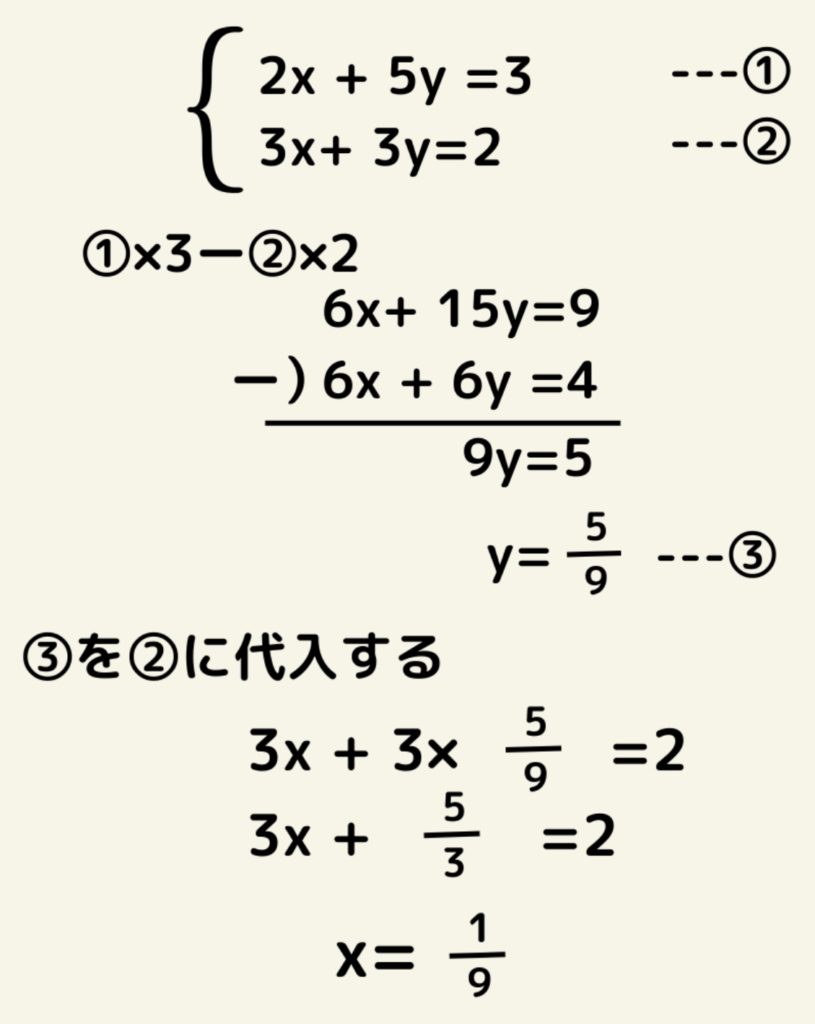
よって答えは(x,y)=(1/9,5/9)になる。
y=,x=になっている連立方程式
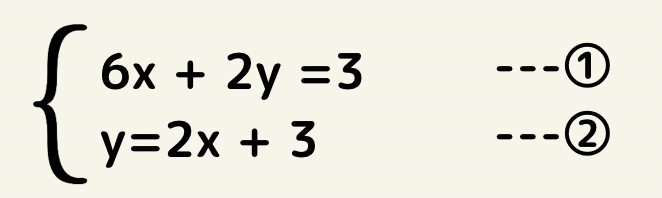
この場合は②の式を①に代入する方が良いと思います。
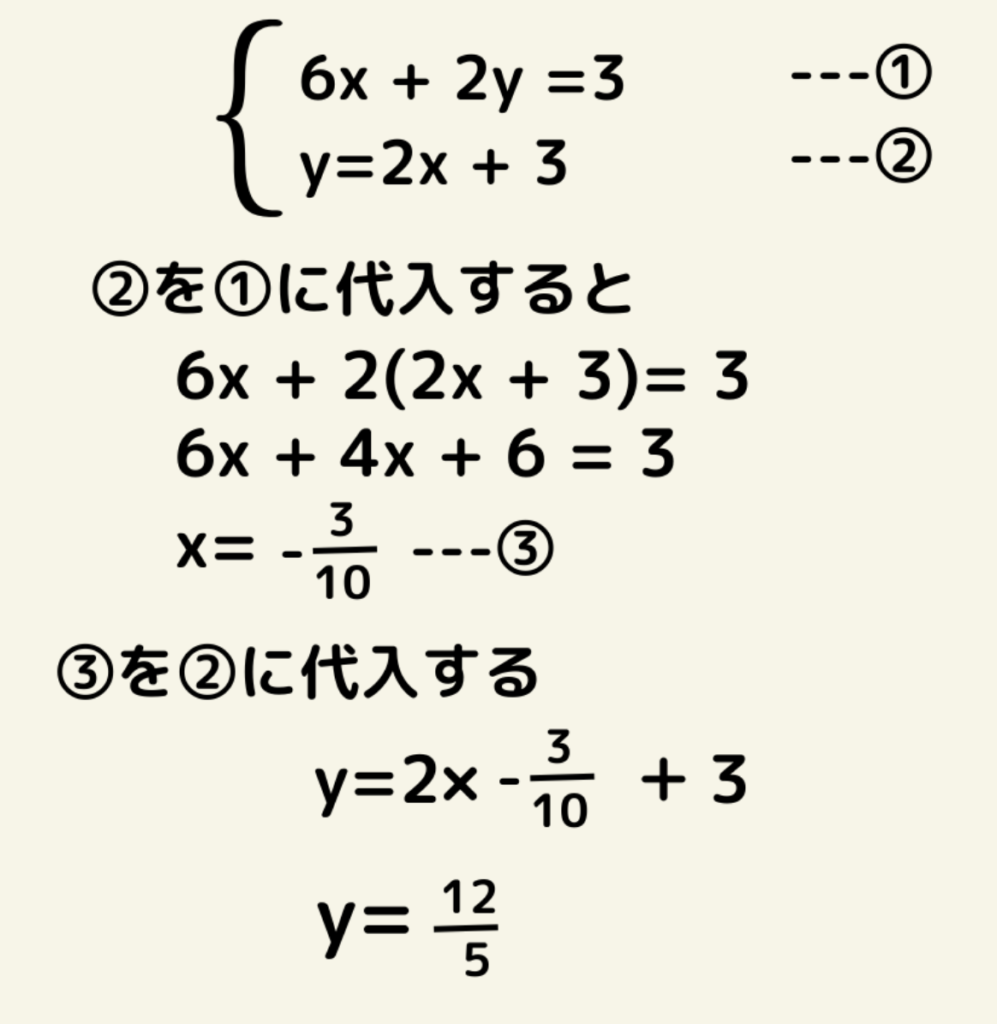
よって答えは(x,y)=(-3/10,12/5)となる。
少数や分数が混じっている連立方程式
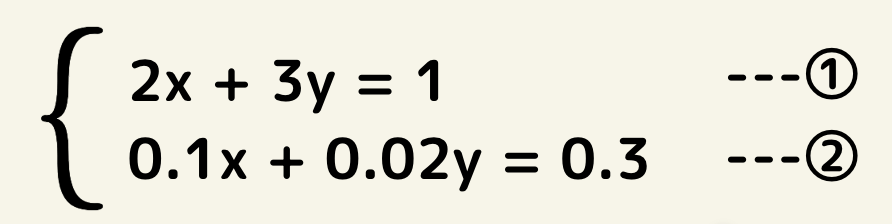
少数や分数が混じっている問題は先に式を整数だけの形に式変形してしまおう!
②式×100をすると
10x + 2y =30 となり、
さらに、全体を2で割ると
5x + y = 15となりかなり計算がしやすくなる。
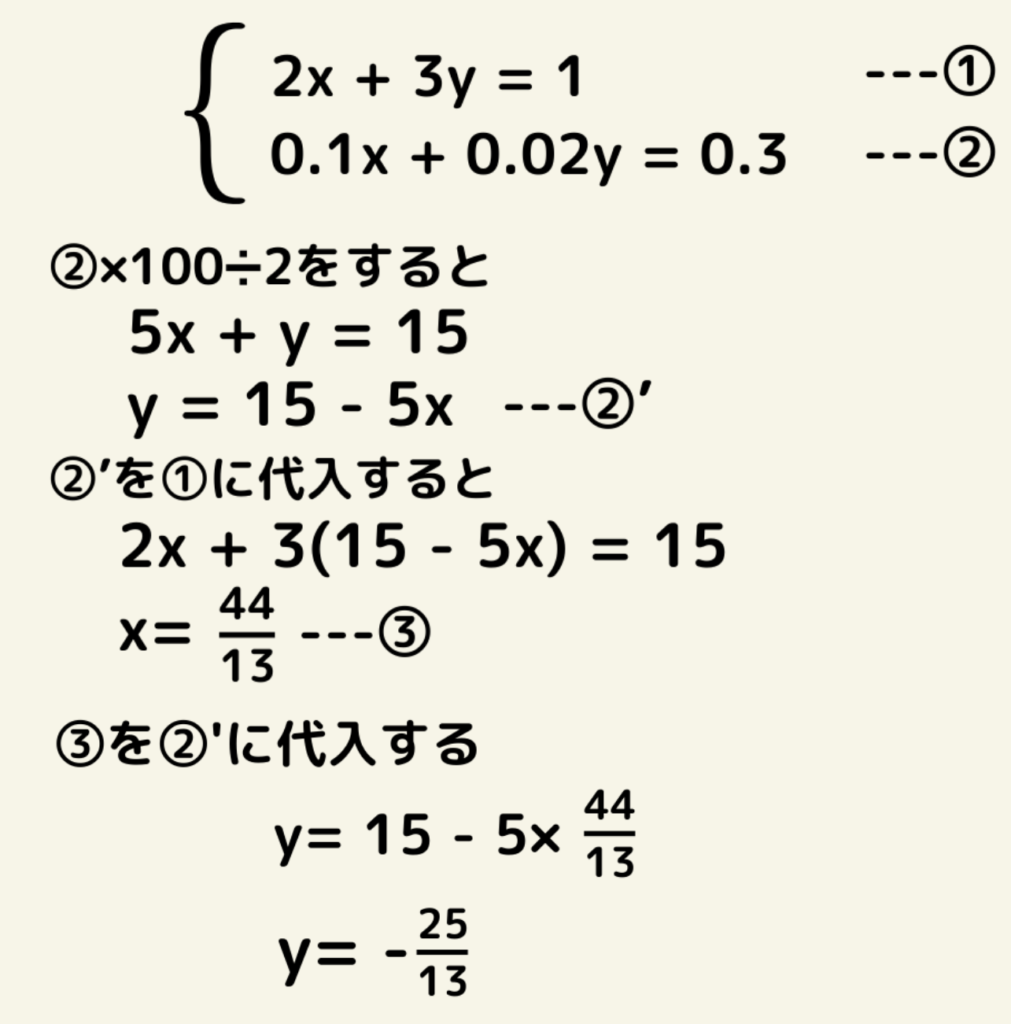
よって(x,y)=(44/13,-25/13)となる。
分数の時も同様で分母の最小公倍数を全体にかけて式を整理してから加減法か代入方で計算をしましょう!
計算の得意な人はいかに計算を楽にするか?を考えている人が得意とする分野なので、ぜひ効率化を目指して頑張ってみてください!
=が連なっている連立方程式
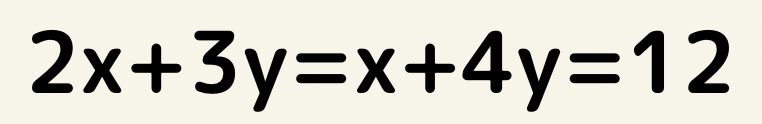
この場合は、切り離して連立方程式を作りましょう!
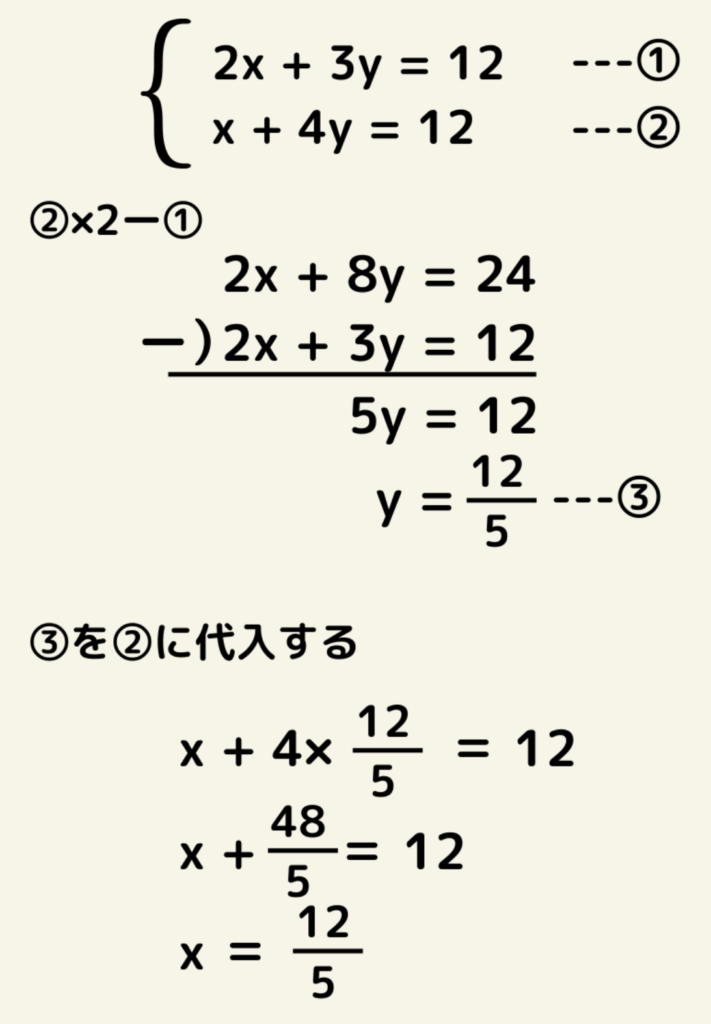
連立方程式が出来てしまえばあとは同じように解くだけです^^
比例式が混ざった連立方程式
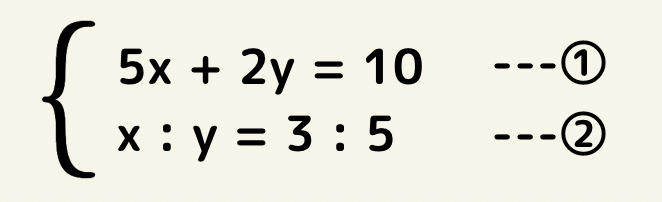
比例式は内×内=外×外で求められるので、②の式を先に整理しましょう。
②より
3y = 5x となる。
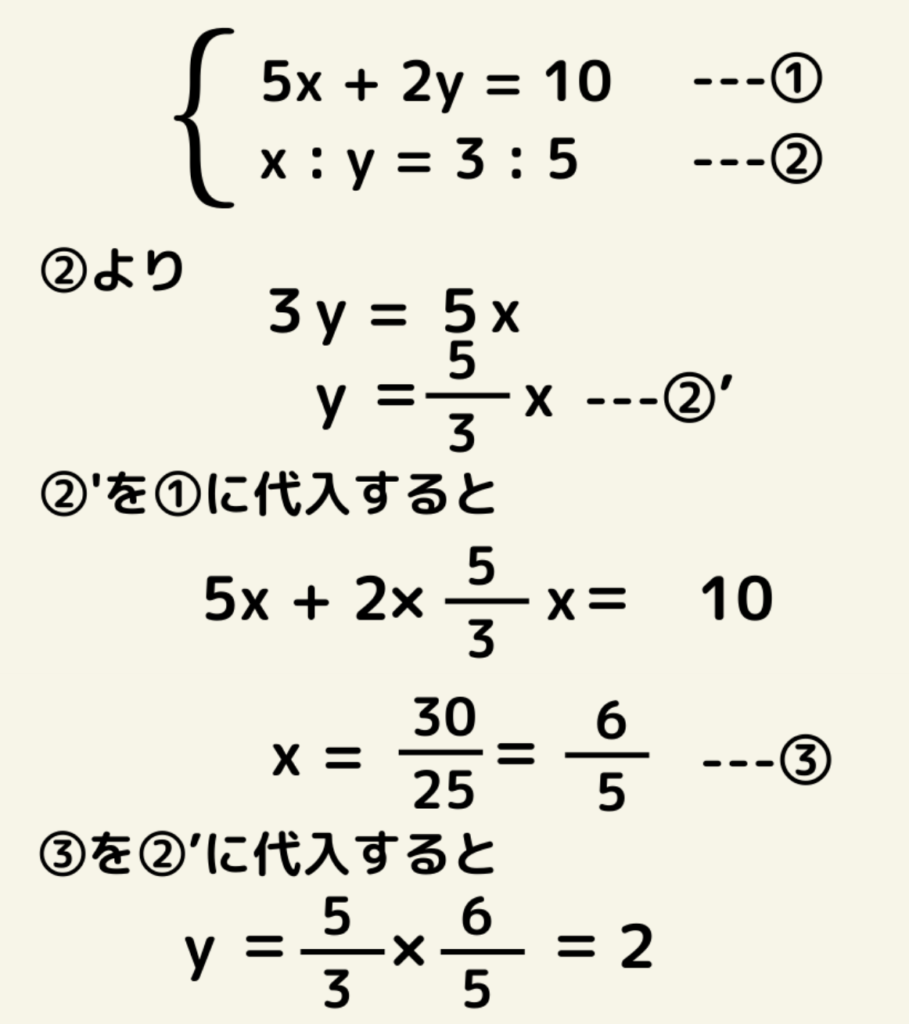
よって(x,y)=(6/5,2)となる。
比例式の問題もまずは連立方程式の基本形に戻してから計算をしよう!
解からa,bを求める連立方程式

このような問題があった時は、まずx,yの解を①、②それぞれに代入してaとbだけの式にしよう!
①式より
2a + (-1) = 2 だから a=3/2
②式より
2a + b = 6 a=3/2なので、代入すると、
2×(3/2) + b = 6
b=3
よって(a,b)=(3/2,3)となる。
今回の問題は①の式にaしかなかったのでスムーズに解けましたが、①と②両方にa,bが存在する場合はa,bの連立方程式を解くこととなります。
x,yがa,bに変わるだけですので今まで同様、基本形で解くことが出来ます。
連立方程式文章題解き方のコツ
連立方程式の文章題で重要な事は問題のイメージができているかです。
必ず次の2つを意識してください。
・何をx,yに置くのか?を明確にする。
・速さや濃度の問題などは図示して解く事を徹底する。
それでは良くある文章題をやってみましょう!
問題1(個数を求める問題)
1個40円のりんごと1個50円のいちごを合わせて10個買ったら代金の合計が470円になった。りんごといちごはそれぞれ何個買ったでしょうか?
解答
方針:りんごをx個、いちごをy個とし①個数の合計 ②料金の合計の2つの式を立てる。
りんごをx個、いちごをy個買ったとする。
個数について:x + y = 10
合計金額について:40x + 50y = 470
連立すると

つまり りんご3個 みかん7個を購入した。
表で考えてもわかりやすいのでおすすめです。

迷った時は活用しよう!
問題2(距離を求める問題)
家から学校まで840mある。
途中の公園まで分速40mの速さで歩き公園から学校まで分速60mの速さで歩いたら合計で17分かかりました。家から公園まで、公園から駅までのそれぞれの距離を求めなさい。
解答
方針:図示して全体像を把握する。家から公園までをxm、公園から学校までをymとおき、①全体の距離 ②かかった時間の2つの式を立てる。

家から公園までをxm、公園から学校までをymとする。
全体の距離:x + y = 840
かかった時間:40/x + 60/y = 17

よって、家から公園までは360m、公園から学校までは480mある。
問題3
2桁の自然数があり、十の位は一の位の2倍より1小さい。
十の位と一の位の数字を入れ替えてできる数は、元の数より9小さい。
元の数を求めなさい。
解答
方針:十の位をx、一の位をyとおき立式する。もし分かりにくければ実際に数字を当てはめてイメージを作りやすくする。
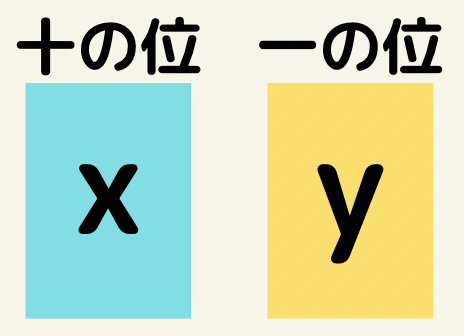
十の位をx、一の位をyとおく。
十の位は一の位の2倍より1小さい
→x = 2y – 1 と表すことができる。
十の位と一の位の数字を入れ替えてできる数は、元の数より9小さい
→10y + x = 10x + y -9と表す事ができる。
ここでのポイントは2桁の数字の表し方です。
例えば51という数字があったとき10の位は5、一の位は1ですね。
51=5×10 + 1 と表すことが出来ます。
つまり、2桁の整数は10x + yと表すことが出来ます。
一の位と十の位を逆にした場合は、10y + xと表せます。
もし文字でのイメージが掴みづらい場合は、数字を当てはめてみて、確認をしてください。
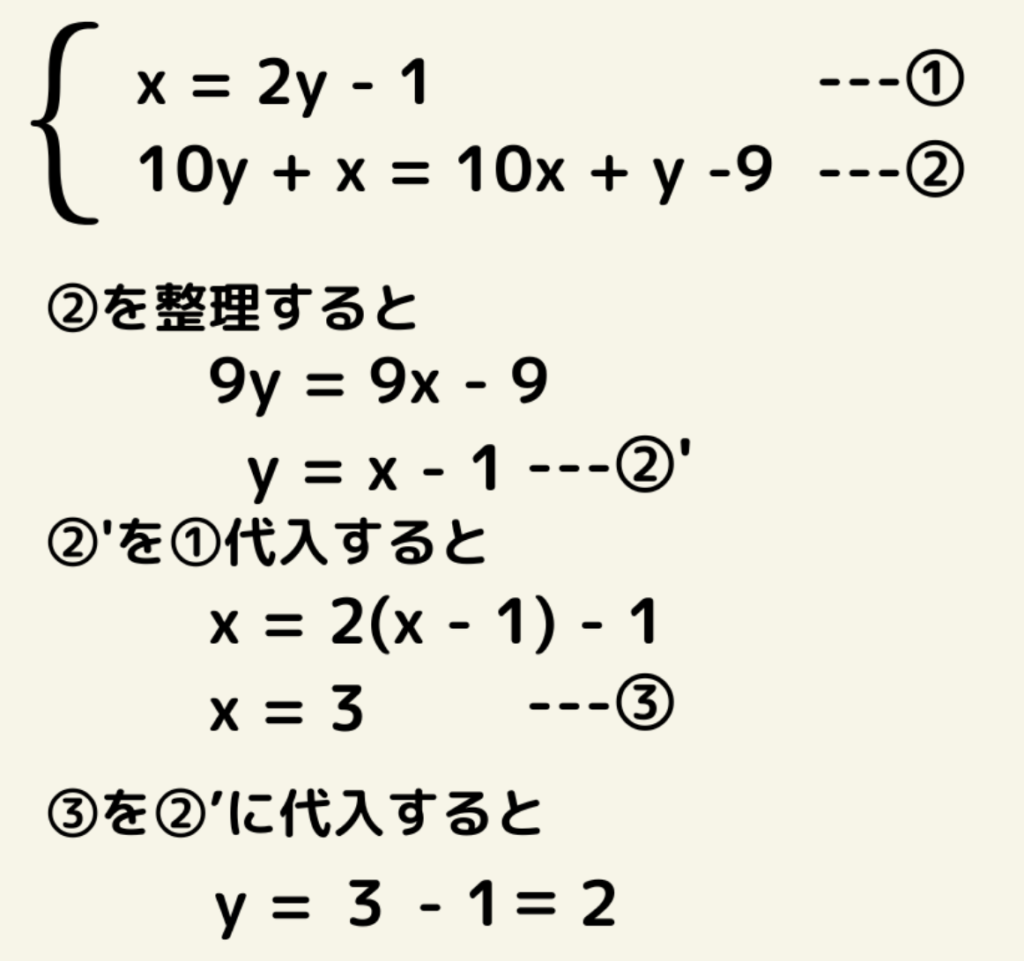
つまり、元の2桁の自然数は32である。
問題4
ある列車が1200mのトンネルに入り始めてからで終わるまでに65秒かかった。
同じ速度で500mの橋を渡り始めてから渡り終わるまで30秒かかった。
この列車の長さと速度を求めよ。
解答
方針:列車の長さをxm,速度を秒速ymとする。トンネルの場合と橋を渡る場合で連立方程式を作る。
今回の問題は、列車の長さがポイントです!
列車がトンネルを通る、橋を渡るというのは、
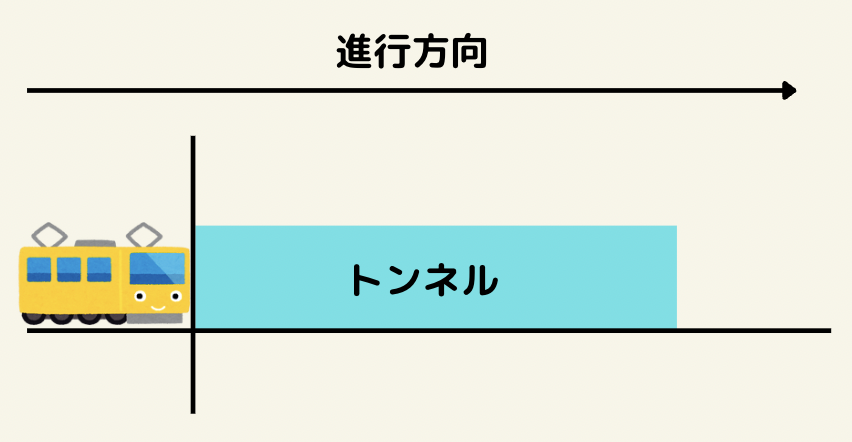
列車がトンネルや橋に差し掛かった瞬間から、
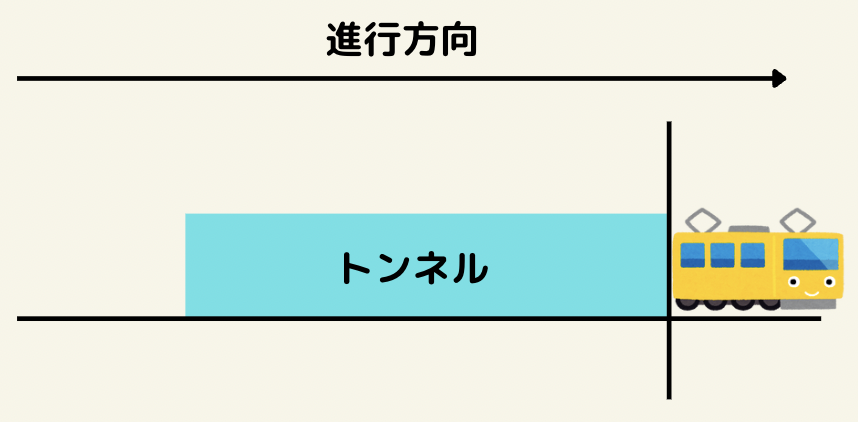
列車がトンネルから完全に出たときまでの事を言うので、
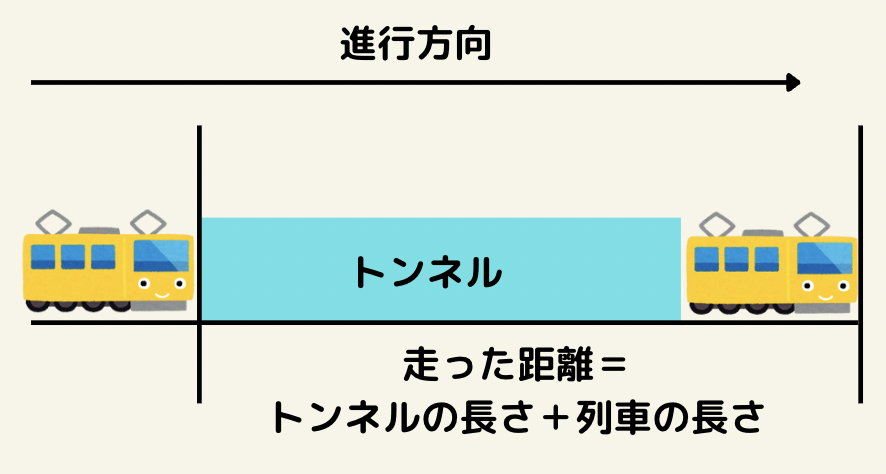
列車が走った距離はトンネル(橋)の長さ+列車の長さとなる。
列車の長さをxm,列車の速度を秒速ymとすると、
トンネルを通る式

なので、65y = 1200 + x
橋を渡る式

なので、30y = 500 + x となる。
連立方程式を計算すると、

つまり、列車の長さは100mで速度は秒速20mである。
問題5
濃度が2%の食塩水Aと8%の食塩水Bを混ぜ合わせて5%の食塩水300gを作った。
それぞれの食塩水を何gずつ混ぜ合わせたか求めよ。
方針:混ぜる前と後では食塩の重さ、食塩水の重さは変わらない。Aの食塩水をxg、Bの食塩水をygとして、①食塩の重さ②食塩水の重さの2つの式を立て連立する。図示するのがおすすめ。
食塩水Aをxg、食塩水Bをygを混ぜ合わせたとする。

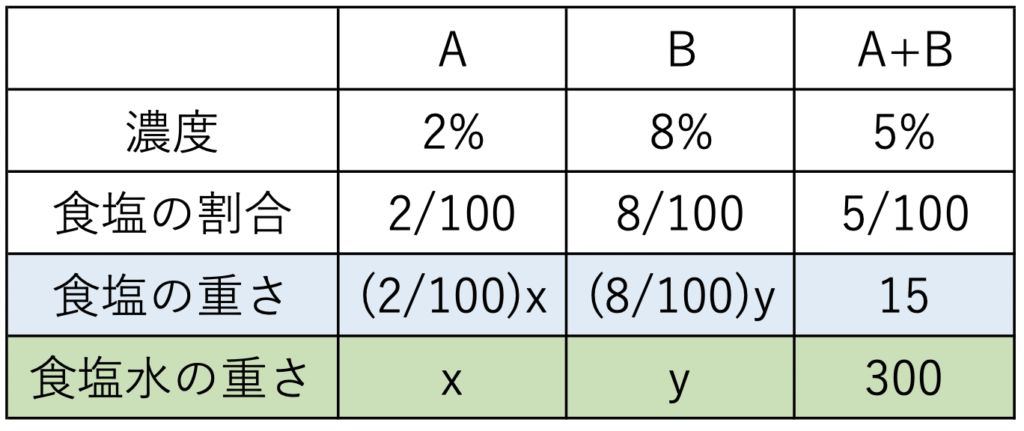
このように図示したり表を作るとわかりやすい。
求める式は
①食塩の重さについて
(2/100)x + (8/100)y = 15
②食塩水の重さについて
x + y = 300
この2式を連立する。

よって食塩水Aを150g、食塩水Bを150g混ぜ合わせると良い。
今回は連立方程式について詳しく解説してみました。
これで夏休み明けの授業もバッチリですね!
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
今日の数学 解答



