数学コラムの目次
今日の数学問題#049
上下の直線が並行で一方の三角形の面積が18cm^2の時、黄色の三角形の面積は?
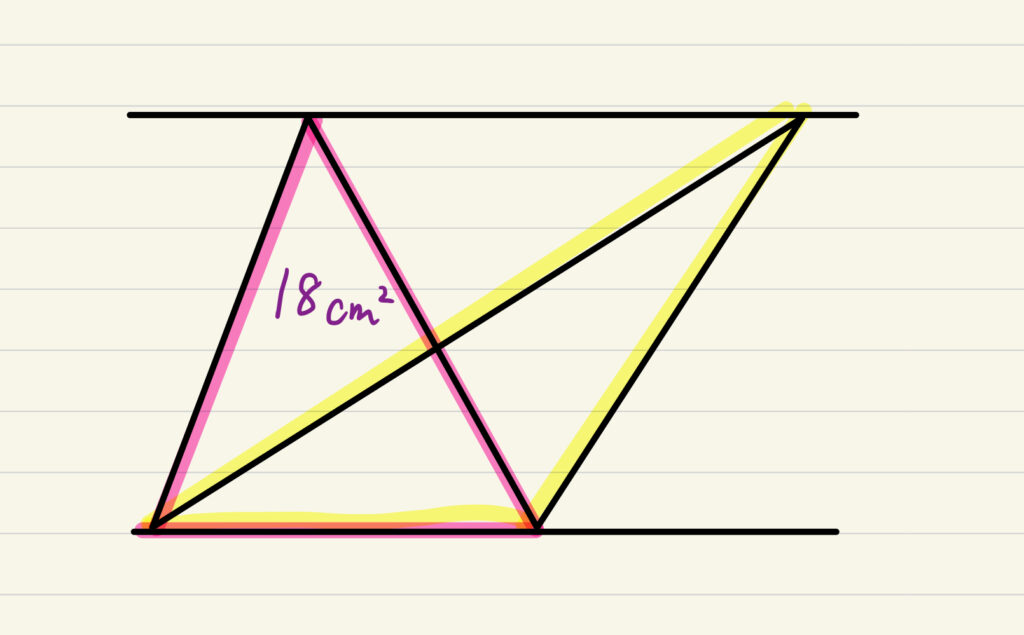
今日の数学コラム
4番セカンド牧
DeNAの4番に2年目の牧が定着しそう^^
セカンドの強打者が日本では少ない印象、最近でこそ、山田哲人選手がいるがプロ2年目での4番はすごいこと。
ベイスターズの4番セカンドって、個人的にローズが思い浮かぶんですが私だけでしょうか?汗
諦めなきゃ何とかなる
話は変わって…僕も野球歴だけで言うとそこそこ長くて、小学4年生の終わりから初めて今もまだ続けているからかれこれ、20年は野球を続けている。
続けているとは言っても途中で辞めたりとかしているので、部活動としてやっていた期間は短い、ただ自分の経歴を話す事でちょっとでも悩んでいる学生さんの力になれればと思う。
小学校の時、野球を始めたきっかけは近所のお兄さんでした。
元々僕自身は何やっても続かないと言われてたくらい飽き性で、水泳をやってた時も伏し浮きが出来ないから、コーチに怒られるからと言う理由でやめた。
だから、僕が野球やりたいって言った時も両親からは反対されていたが、4年生の終わりくらいにたまたま近所のお兄さんが紹介してくれて、クラブチームの体験に参加した。
それからは野球にどハマりして、不器用ながらも楽しいから頑張れた。
ただ超がつくほど下手で不器用だったのは間違いない笑。
まさに打てない・守れない・走れないの3拍子揃った選手だった笑
ただ、なぜか今回は諦めなかった。
下手だと言われても純粋に野球が楽しかったからだと思う。極度の怖がりで打席に立つたび震えていたけど、初めて6年生になってヒットを打った。
友達もでき病気がちだった身体もしっかりしてきて超健康体に。
中学も続けて野球部に入った。
中学生時代
中学校に入ると球拾い期間の後、1年生も数名練習に参加できるようになる。
なぜかそこに選ばれた僕。
当然のことながら体が震えて試合に出たらエラーはする、ボールには当たらない。
当然試合に出れなくなった。だけど不思議な事に最終打席で強烈なライトライナーを打ったことだけは覚えてる。
「なんでお前が選ばれんねん、下手くそやのに」
友達にもそう言われた。
あとは自分なりにコツコツ練習していて迎えた2年生の時、いきなり打てるようになった。
これがなぜかわからないのだけれど、ボールがめちゃくちゃ見えるようになった時期があった。それからちょくちょく試合で使ってもらえるようになって背番号ももらった。
秋の大会で12打数8安打を記録。完全に人生のキャリアハイ笑
3年になって近所の強豪クラブチームが内部分裂し、半数名がうちの野球部に入部し、ベンチウォーマーと化した僕は腐りかけてましたが、最後まで何とかやり切りたいという思いだけで中学野球を完遂。
高校生時代
高校へ入り野球するつもりはなかったんですが、見学に行ったときにやっぱりやりたくなって、入部しました。
ただ、1年生の夏に体を壊してそのまま退部をします。
この時期はめちゃしんどかったですが、リハビリしながら何とか卒業し近畿大学へ進学。
大学生時代
大学では軟式野球部に入ることを決めました。
理由は中途半端で終わったので諦めきれなかったのとやっと身体が動くようにでと思って入部しました。
大学2回生の時に投手に転向して、そこから今までず〜っと投手。
案外投手になったのが良くて、この時に実は器用だったんじゃないか説が浮上。
クセ球のストレートや変化球は一通り投げられて、「よくそんな球投げられるな」と言われていた。
ただ、3回生の時、イップスを発症。キャッチボールすらままならなくなり、そのまま引退を迎えた。
そして、現在
社会人になって草野球をやりながら仕事に没頭していると、なぜか投げられるようになり、クラブチームに移籍そこから今に至るのだが、、、
こうやって書いてみると驚くほどにメンタルに引っ張られているな〜と感じる。
その経験があったから今はメンタル面のサポートをトップアスリートにもできてるんだと思うんだけど^^;
経歴だけ見たら全然ダメダメでも実は大人になってからやり方次第で大きく変わることが出来る。それは僕自身が体感しているし、まさか学生の時の僕が今のようにメンタルの先生や塾をやってるなんて誰も想像つかなかっただろうと思う。
「お前ほんまになんもできひんな」
そう言われ続けてきたから。
だけど諦めずにコツコツと努力して人を頼って食らいついて行ったら何か見えてくる部分が絶対にある。
だからもしこのブログを読んでいる方の中で同じように挫折している人がいたら諦めないでほしい。
大丈夫。やり方次第で何とかなる。
以上。
今日はすごく真面目な話をしてしまいました笑
京都市中京区のアイデア数理塾 油谷でした!
今日の解答#049
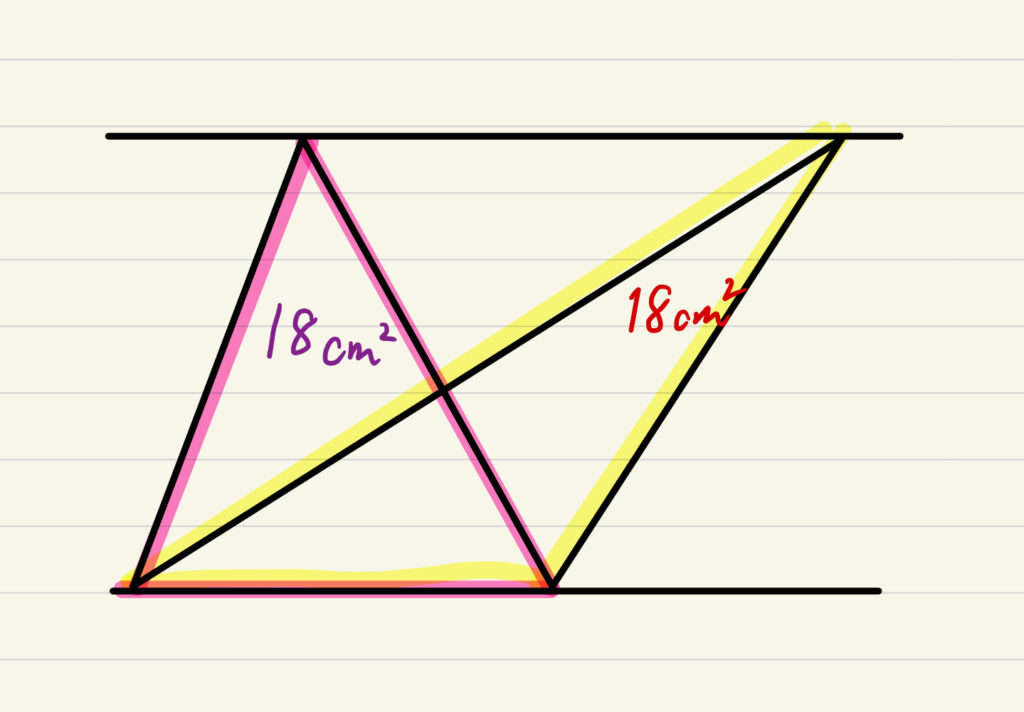

三角形の面積は底辺×高さ÷2で求められる。
今回は上下の直線が並行なので高さが同じで底辺も同じなので、面積自体も同じになる。
つまり一方の三角形が18cm^2だから黄色の三角形も18cm^2になる。


