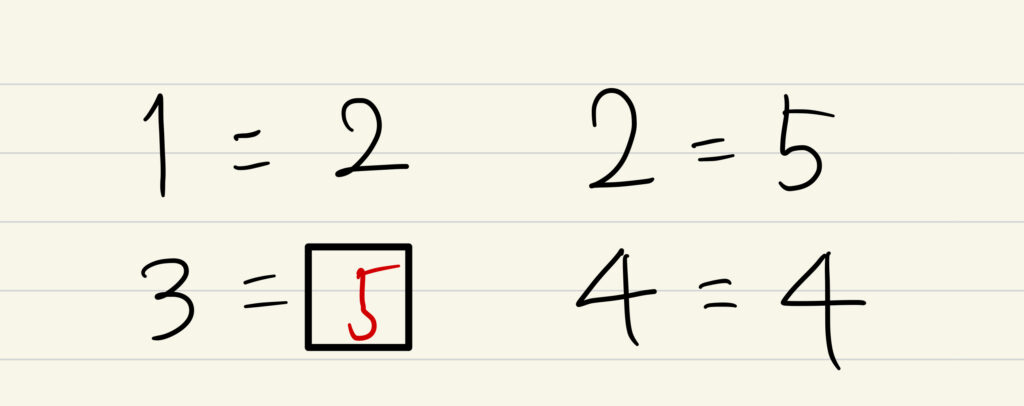数学コラムの目次
京の算数学問題#008
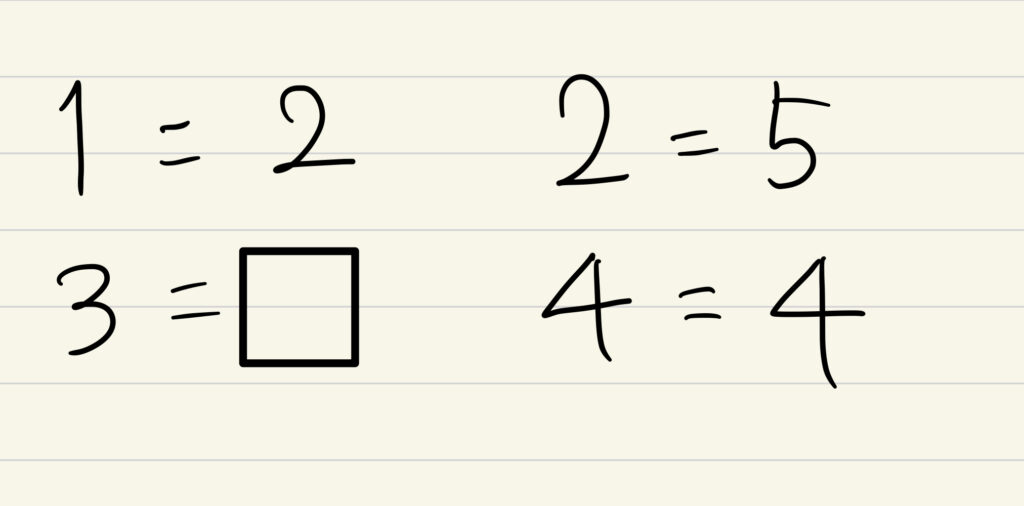
今日の問題はなぞなぞです!
法則を見つけましょう!
アイデア数理塾はこちら
算数学コラム
今日は個人的に好きな数学の雑学を紹介していきます!
知ってるものはあるかな??
それでは今日もいってみましょう!
数学雑学って個人的には小学校ぐらいからかな?
周りでも流行っていて、特に誰から聞いたでもなくなぜかみんな知ってたようなものってありますよね。
例えば18782(いやなやつ)を2回足したらとか笑
小学生って面白くて当時今みたいにネットで何でも載ってる時代じゃなかったのに何であんな詳しいのかね?笑
誰か教えてください笑
142857(石には粉)の不思議
この不思議な数字に1から順にかけて行ってみましょう。
どんな変化があるのか?
142857×1=142857
142857×2=285714
142857×3=428571
142857×4=571428
142857×5=714285
142857×6=857142
お気づきになられましたか?
そう142857が後ろにずれているのです。
さらに×7をすると?
142857×7=999999
なんと!9が並びましたね!
まだまだ秘密があります。
142857と上記の1〜6をかけた数字を半分にして足してみましょう。
142+857=999
285+714=999
428+571=999
571+428=999
全て999になるのです!
これを証明しているサイトもあるので、もし興味があればぜひ検索してみてください!
これが解けたら1億円?!
2000年5月24日アメリカのクレイ数学研究所は「ミレニアム懸賞問題として」それぞれに100万ドルの懸賞金をかけたとのこと。
ちなみにその問題の1つであるポアンカレ予想は既に解決されています。
紙を何回折ると月に届く?
紙を半分に折ってさらに半分に折ってと乗数的に厚さが増していくと、なんと42回で月に届くと言われています。
ただ実際にはそんなに折れませんよね^^;
あくまで理屈上はという話です笑
小学生時代の僕は実際にチャレンジしてみたことがあるのですが、6回ぐらいで断念しました笑
面白数学用語
セクシー素数
差が6の素数の組のこと
ナルシシスト数
n 桁の自然数であって、その各桁の数の n 乗の和が、元の自然数に等しくなるような数
結婚定理
組み合わせ数学の一つで、ホールが証明した定理が成り立つことと、女性の要望に沿ったマッチングが存在することは同値だという。詳しくは結婚定理で調べるとややこしい証明が出て来ます笑
東京大学入学試験で出題された伝説の問題
「円周率が3.05より大きいことを証明せよ。」
この問題ってすごく核心をついていて、中学生までに習った内容で解けてしまうんです。
3より大きいは簡単なのですが、3.05以上というのがやらしいですねえ笑
この問題のポイントは、「円周率って何か説明できるの?」という
ところでしょうか。
円周率ってそんなに深く考えたことないと思うんですよ。
3.14!とは答えられても、円周率って何?が答えられる人は少ない、、、
円周率は円の直径に対する円周の長さの比率です。
円周➗直径で求めることができます。
これを発見したのはアルキメデスと言われていて、当時は3.14ではなく22/7を使っていました。
ちなみに円周率のπとはギリシャ語でπεριμετρου(周の意味)の頭文字を取ったものです。
このように実は日本トップクラスの入試は本質を問う問題が多いのです。
ただ問題を解くだけでいいのではなくなぜこうなるのだろう?とか公式ってどうやってできるのだろうとか理解していると全然解法やひらめきが変わって来ます!
小学生からできる楽しい数学
数学はある意味実験と似ている部分があります。
その一つが統計です。
例えばじゃんけんの手の出し方は1/3ですが、11567回のジャンケンデータを集めるとグーが一番勝率が高かったそうな。
気になったことを何回か同じことをしてみて確かめてみる。
これが実験です。
何回かチャレンジしてみると新たな疑問も湧いて来ます。
あ!ここでこれやってみたらどうなるだろうか?
あそこがミスだなとか
小学校の算数は一度やってみるというところをポイントにしてみましょう!
面積の求め方も画用紙を繋いでみたりとか、四角形の求め方も三角形を2つくっつけてみるとか、実はやって見るとノートでやるよりもはるかに定着しやすいことがわかります。
是非一度チャレンジしてみましょう!
京の算数学 解答#008
今日のポイント!
身近にあるものに答えが、、、

そう!答えはデジタル時計に隠されていました!
1はデジタルで棒が2本必要です。
同様に2は5本必要ですよね!
なので3は5本必要になります!