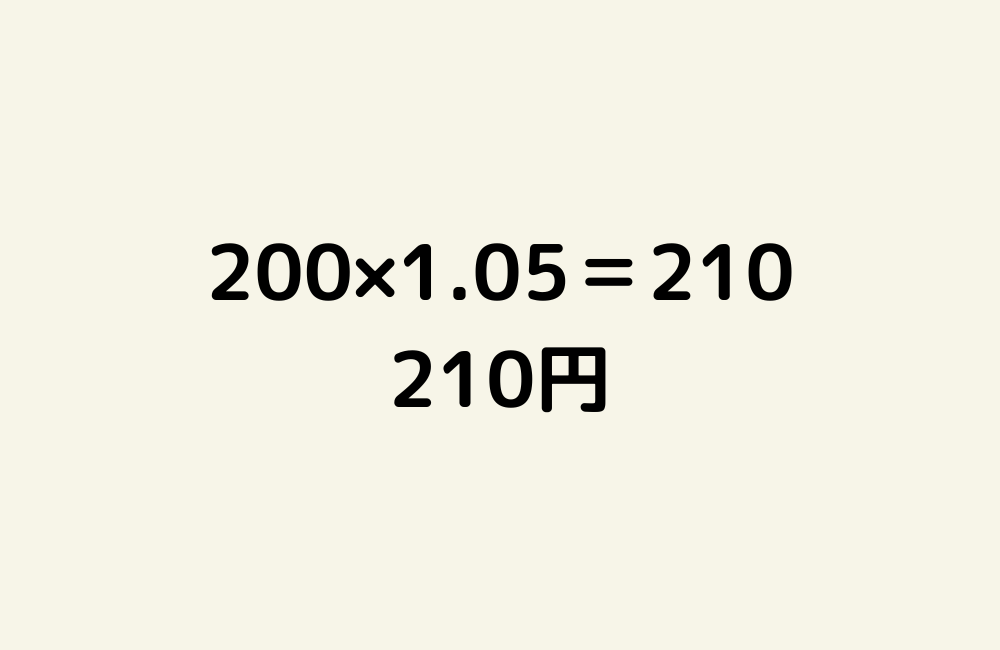数学コラムの目次
京の算数学問題#761

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
小学5年生になると、算数の授業で「割合」が登場します。割合は、日常生活でもよく使われる重要な概念です。しかし、初めて学ぶときには少し難しく感じることもあるでしょう。今回は、割合の問題を解くコツをわかりやすく解説します!
割合の基本とは?
割合の意味
割合とは、全体に対する部分の大きさを表す数値です。例えば、クラス全員のうち男子の割合や、リンゴ全体のうち青いリンゴの割合など、部分が全体のどれだけを占めているかを示します。
割合の表し方
割合は百分率「パーセント(%)」や「小数」で表すことができます。例えば、50%は0.5とも表せます。また、分数で表すことも可能です(例:1/2)。
割合を求める公式
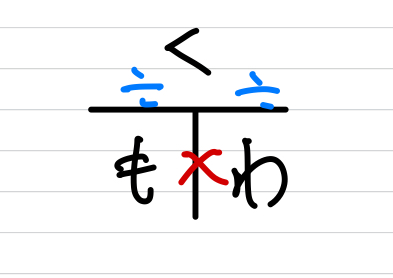
く→比べる量
も→もとにする量
わ→割合
例えば割合=比べる量÷もとにする量ですし、比べる量=もとにする量×割合となります。
まずは基本となる公式は押さえておきましょうね。
具体例
クラスに40人の生徒がいて、そのうち10人が男子だったとします。男子の割合は次のように求められます。
この時の男子の割合は、10÷40=0.25となります。
百分率で表すと0.25×100=25%となります。
百分率ってなに?
私たちが最初に習う割合の問題は小数で答える場合が多いです。
それはもとにする量(全体の量)を1とした時に比べる量がどれだけあるのか?ということです。
例えば、クラス30人のうち理系が3人だったら3÷30=0.1となります。
ただ、小数で表した場合わかりにくくないですか?
なので、もとにする量を100とした時に全体のどれだけあるのか?を考えてみましょう。
この場合0.1がクラス1人あたりにおける理系の割合なので×100をすると、10%となります。つまり100人のうち10人が理系であるのと同じであるといえます。
こうすればわかりやすいですよね。
割合の問題を解くコツ
コツ1 文章の「割合」の前がもとにする量
文章題においてまず重要なのは全体が何なのか?つまりもとにする量を考えることです。
例えば、たろうくんの1ヶ月のお小遣いは700円で、けんたくんの1ヶ月のおこづかいの1.4に当たるそうです。けんたくんのおこづかいは?
文章題においては割合の前に来るものがもとにする量になります。
この場合1.4というのが割合なので、けんたくんの1ヶ月のおこづかいがもとにする量になります。
つまり、今回の問題は「けんたくんのおこづかい」を求めたいので、もとにする量を求めたい問題であるということがわかります。
よって、700÷1.4=500円が答えになります。
コツ2 公式を覚える
割合を求める公式「く・も・わ」をしっかりと覚えましょう。
この公式を使いこなせれば、どんな割合の問題でも解けるようになりますので、まずテストの答案用紙に書いておくなど、しっかり活用していきましょう。
コツ3 図で考える
割合は図を用いると理解しやすい場合が多いです。
例えば、クラス30人のうち理系が3人だったら
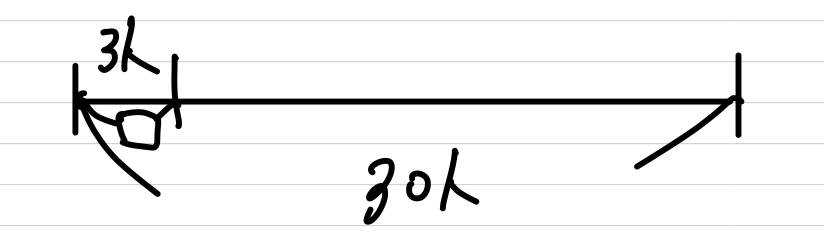
たろうくんの1ヶ月のお小遣いは700円で、けんたくんの1ヶ月のおこづかいの1.4に当たるそうです。けんたくんのおこづかいは?
この場合だと、
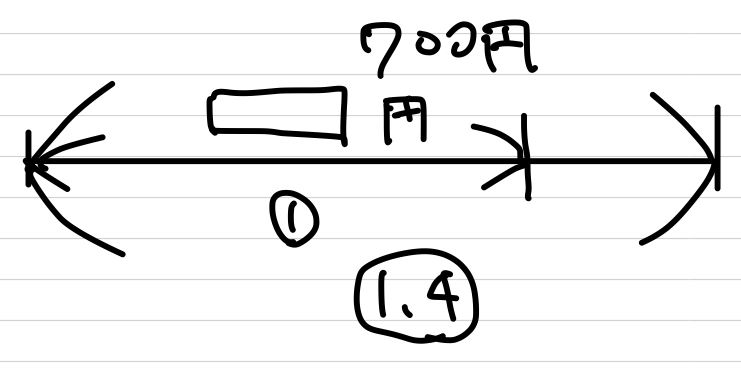
図を書くことで文章を整理していきましょう。
まとめ
割合の問題を解くためには、く・も・わの公式を理解すること。
そして文章題においては何がもとにする量なのか?を把握することを最初に行いましょう!また、図を書くことも効果的です。たくさんの問題に挑戦し、割合のマスターを目指しましょう!
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#761