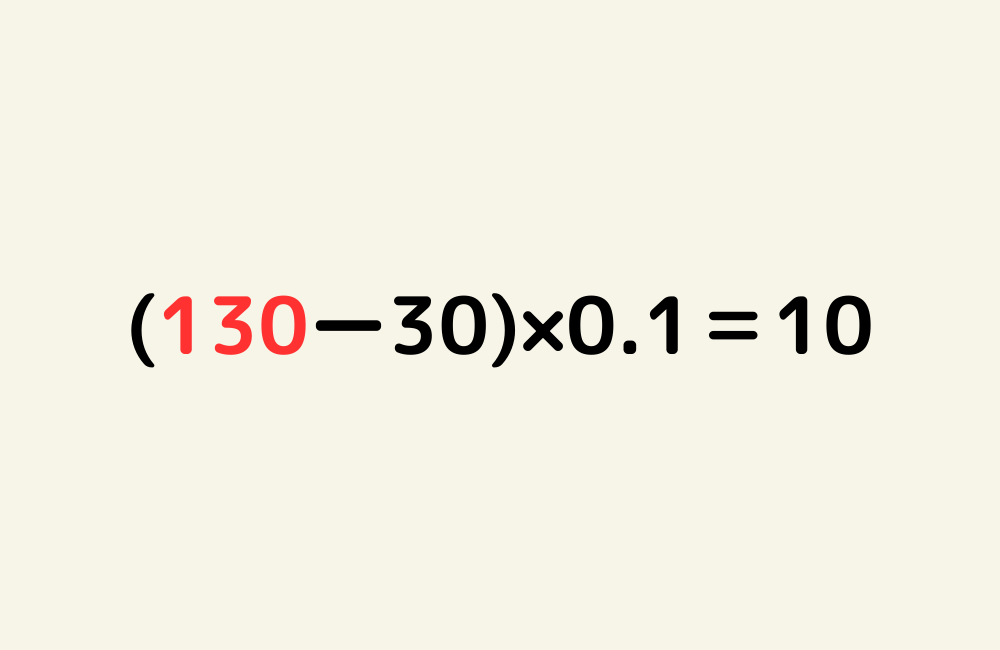数学コラムの目次
京の算数学問題#660

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
中学数学において素数という初めて学ぶ世界は、興味深く非常に奥が深い考え方です。
今日は素数の基本についてお話をしていきます。
素数はなぜ見つかった?
素数とは2,3,5,7のように、1とその数でしか割り切れない自然数の事です。
素数の発見は記録に残る限り紀元前3世紀あたりに古代ギリシアのユークリッドがまとめた数学書である言論に「素数が無限に存在する」という事が証明されています。
小学生でもできる!素数の見つけ方
素数の見つけ方は九九がわかっていれば導き出す事ができます。
エラトステネスのふるいと呼ばれるこの方法は、1を除く2〜20の整数を順番に書いていき、2は残したまま2の倍数を消していきます。
次に3を残したまま3の倍数を消していくというふうに少しずつ素数を絞っていきます。
①2〜20までの数字を書き出す
2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20
②2を除く2の倍数を消していく
2、3、5、7、9、11、13、15、17、19
③3を除く3の倍数を消していく
2、3、5、7、11、13、17、19
④残ったものから5、7を除くそれぞれの倍数を消していく(今回は無い)
⑤残ったものが素数
2、3、5、7、11、13、17、19
1は素数では無い理由とは?!
素数の定義では1は素数ではありません。
素数には一意性という考え方があります。
一意性とは存在するとしたら「ただ一つだけである」という考え方です。
例えば6であれば、10=2×5で表す事ができます。
ここに1が入ると10=2×5×1×1×1×、、、というように、いくらでも1をかける事ができてしまいます。
このようにいくらでも組み合わせが生まれてしまうことから、1は素数ではないとしたのです。
もちろん素数に関する考え方はいろいろあるのですが、1つの考え方としてご理解いただければと思います^^
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#660