数学コラムの目次
京の算数学問題#585

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
小学校5年生になると勉強する「円」ですが、「円周と面積を求める」という部分で非常に苦労している生徒が多くいます。
今日のブログは円マスターを目指して問題を解くコツをまとめています。
ぜひご参考にしていただければと思います!
円の定義とは?
円とは平面上の定点から等しい距離にある点の集合でできた曲線のことです。
この定点を円の中心と言います。
円の定義と一緒に算数用語も覚えておきましょう。
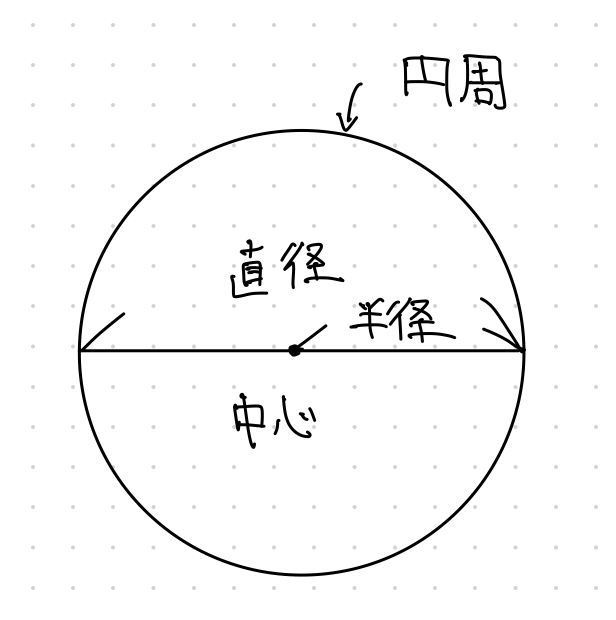
覚えておきたい円の公式
円周=直径×円周率(3.14)
面積=半径×半径×円周率(3.14)
小学校で学ぶ円の公式は中学になっても使用するのできちんと覚えておこう!
円周率ってなに?
円周率とは円の直径に対する円周の長さの比率です。
円周÷直径がおおよそ一定の値になるという意味です。
円周率は3.1415926535……というように永遠に続く無理数ですが、
小学校の単元では主に3.14という値を用います。
(中学に入るとπと文字に置き換えて使用します)
円の問題を解くコツ
算数が苦手な生徒の特徴としてその数字が何を表しているのか?がわからないというものがあります。
算数の世界では2や3という数字で表記されてしまいますので下記のポイントを守りましょう。
1.式に単位を必ず書くこと
2.式を1本にせず1つずつ完結させる
例えばこんな問題
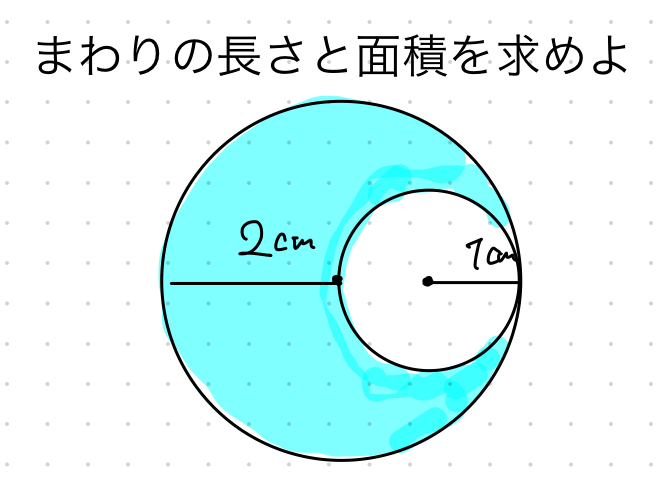
この青い部分の面積は大きな円から小さな円を切り取った問題です。
面積の場合は大きな円から小さな円を引けばいいですよね。
これを1本の式で表すとこうなります。
2×2×3.14―1×1×3.14=9.42
こうなると式も長くなりますし見間違いも増えてしまいます。
また、前の式が何を表しているのか?わかりにくく見えてしまいます。
そこで、下記の用に解いてみましょう。
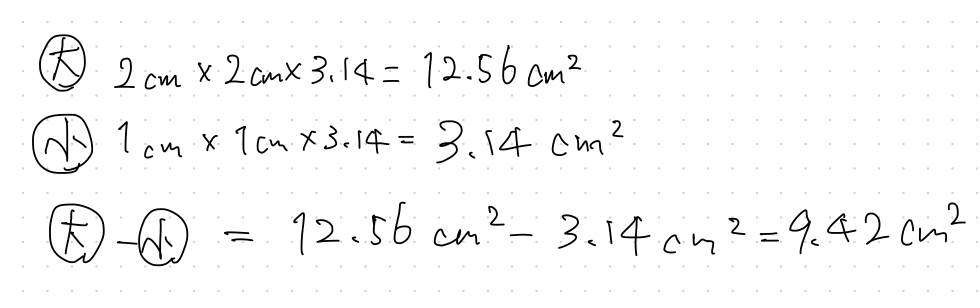
これだと何を求めているのか?明確ですし、式が分解されているので計算ミスも減ります。
次に周りの長さです。
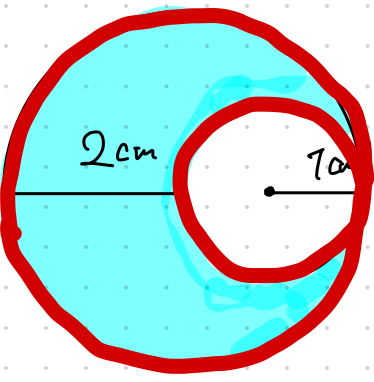
周りの長さとはこの赤く塗ってある部分なので2つの円の円周を求めます。

ここまで丁寧にする必要はないと思われるかもしれませんが慣れるまではここまで手順を明確にした方が結果的に正答率は上がります。
ぜひおためしください!
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#585




