数学コラムの目次
京の算数学問題#338

アイデア数理塾はこちら
算数学コラム
小学5年生の必修範囲である最大公約数はつまづく生徒も多く、
数字が大きくなればどう解いて良いかわからないと
困惑する場面を良く目にします。
でも大丈夫です!
最大公約数のコツがわかれば今まで10分かかっていた問題が3分程度で解けるようになります。
今日は最大公約数の解き方を3つの方法で学んでいきます。
最大公約数ってなに?
最大公約数とは最大の公約数という意味です。
例えば
42という数字があったとします。
42÷1=42
42÷2=21
42÷3=14 など
1,2,3,6,7,14,21,42というような「ある1つの整数を割り切る数」を約数と言います。
20の場合
1,2,4,5,10,20となりますが、
42と20の約数を比べると1,2のように共通の約数が見られます。
このように「2つ以上の整数に共通な倍数」を公約数と言いこのうち最も大きな公約数(42と20の場合は2)を最大公約数と言います。
実際に最大公約数の問題を解いてみよう!
【問題】
次の最大公約数を求めよう!
(42と63)
大きい方の数の約数から考える
まず63の約数を探していきます。
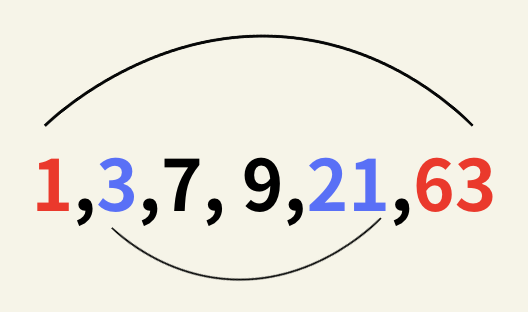
約数はこの図のようにペアになって出てきます。
例えば63=1×63なので言い換えれば1と63が約数と言えます。
約数は何で割れるか?よりもまずは何をかけたらこの数になるか?という発想の方がいいかと思います。
次に42の約数を求めていきます。
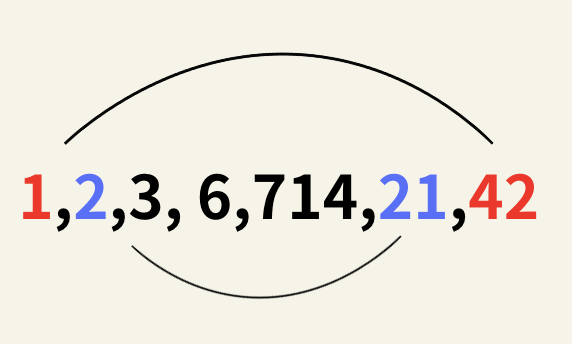
この中で公約数は、
1,3,7,21で最大公約数は21となる。
筆算を使って求める
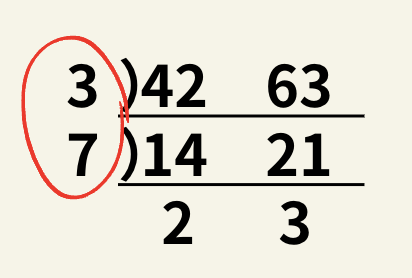
この左の丸の付いている部分をかけると3×7=21となり最大公約数が求められます。
この計算方法自体は求めたい対象の整数を横に並べ(3つ以上でもできます)、共通の割れる数で割れなくなるまで割っていきます。
割る数は大抵、2か3か5か7あたりなので出来るだけ簡単な数字で割っていくと良いです。
素因数分解で求める(中学生向け)
今回の問題だと
63=3×3×7
42=2×3×7
と表す事ができます。
最大公約数は「共通の素因数のうちより小さい方をかけたもの」になるので、
簡単に言えば、今回の場合3×7が共通していますよね。
なので3×7=21が最大公約数となります。
この方法は先日のブログにも書きましたが、筆算の根本的なやり方の解説に当たります。
なのでまずは1つ目のやり方をマスターしてから筆算にチャレンジしてみましょう!
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
京の算数学 解答#338




