アイデア数理塾 今日の問題#128
今日のコラム
「数学で応用がきかないんです、、」
その原因は実は勉強法にあったんです。
通常学校の勉強は基礎定着用の勉強法です。
つまり「言われたことをどれだけ正確に再現できるか？」という再現度を高める勉強法です。
問題集を開き何も見ずに問題を解けるか？という感じでしょうか？
定期テストで点数を取るためとカリキュラムを完遂するために進んでいきますがそれでは応用は効きません。というより素直な生徒ほど応用が効かなくなります。
そこで応用が得意な生徒の答案や解答を分析してみて思考がどうなっているのか？を調べていると重要な事がわかりました。
それは問題の作業工程１つ１つの意味を説明できていることでした。
わかりやすいのが、合同の証明問題。
作業工程を文章化するので、文章丸覚えしている生徒ときちんと理解している生徒の差が明確に現れます。
高校の式の計算や三角関数などは、よりこの「作業工程が説明できること」ができるできないが応用力に関係してきます。
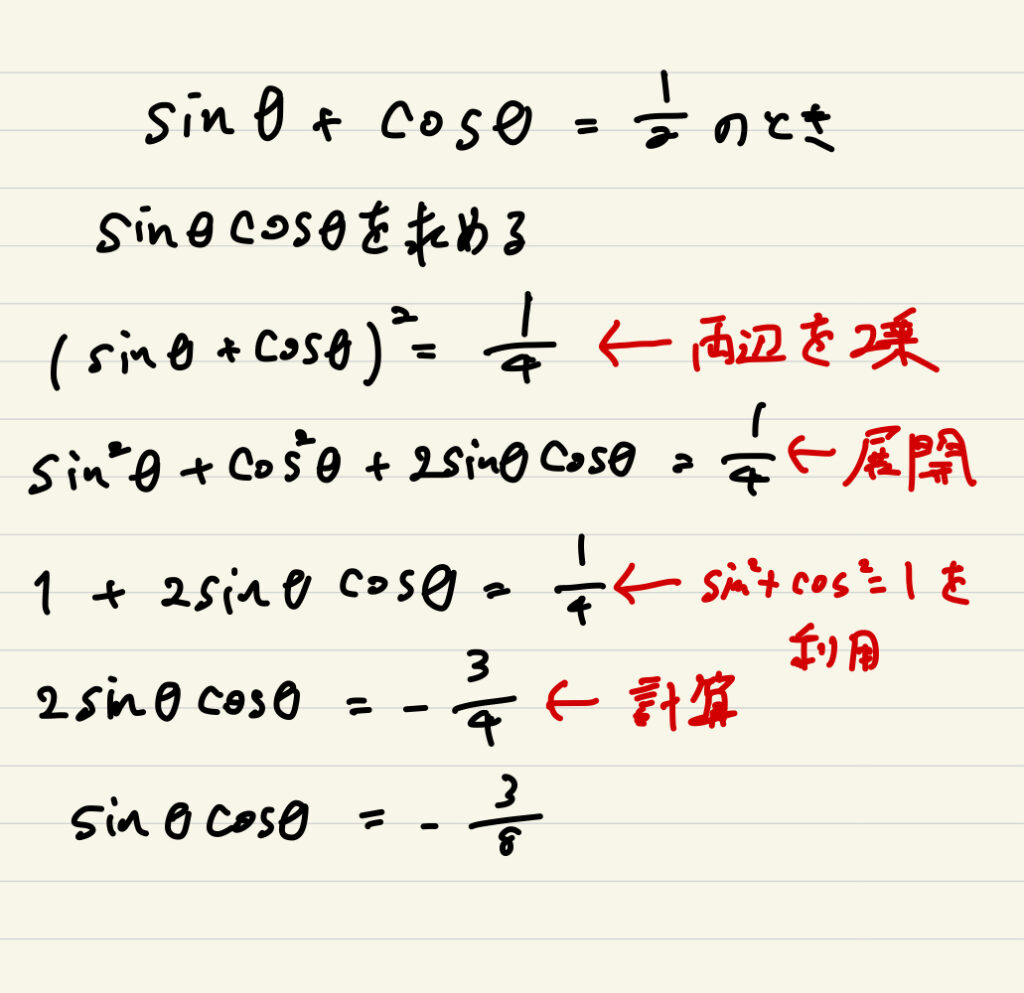
定番の三角関数の相互関係の問題なのですが、「数学できる」という人はこんな感じで、各工程の動作を説明はできると思います。
ただこれだけでは応用が効くとは言えません。
ここからさらにその動作は何のために？したのか？が説明できないといけません。
・両辺を２乗した→sinθcosθの形を作るため
・展開する→展開しないとsinθcosθの形にならないから
・sin^2+cos^2=1を利用→sin^2とcos^2を消したかったから
・計算する→sinθcosθ＝数字 にしたいから。
といったような感じです。
要は操作を覚えるだけではテストの点数は取れても受験では使えないんです、何のためにその操作をしたのかが最重要です。
これから応用力をガンガンつけていきたい方はぜひこの方法を試してみてください^^
以上！京都市中京区のアイデア数理塾 油谷がお届けいたしました！
今日の解答#128
