数学コラムの目次
京の算問題問題#111

アイデア数理塾はこちら
算数学コラム
パラドックスという言葉を知っていますか?
パラドックスとは正しそうに見えるんだけど実はそうじゃないと言うもの。
以前の記事でモンティ・ホール問題を取り上げましたが、あれも1種のパラドックスです。
2=1の証明??
数学の場合、仮説を立てて数字や定理を使い証明をすると言う事で相手にこの仮説は正しいんだ!と言うことを伝えますが、それゆえパラドックスが結構あります。
面白いのが2=1の証明です。
これから2つの方法で証明を行っていきますがそれぞれの前提として
「a=bとする」がありますのでご注意ください。
証明①
a=bのとき両辺にaを加えると
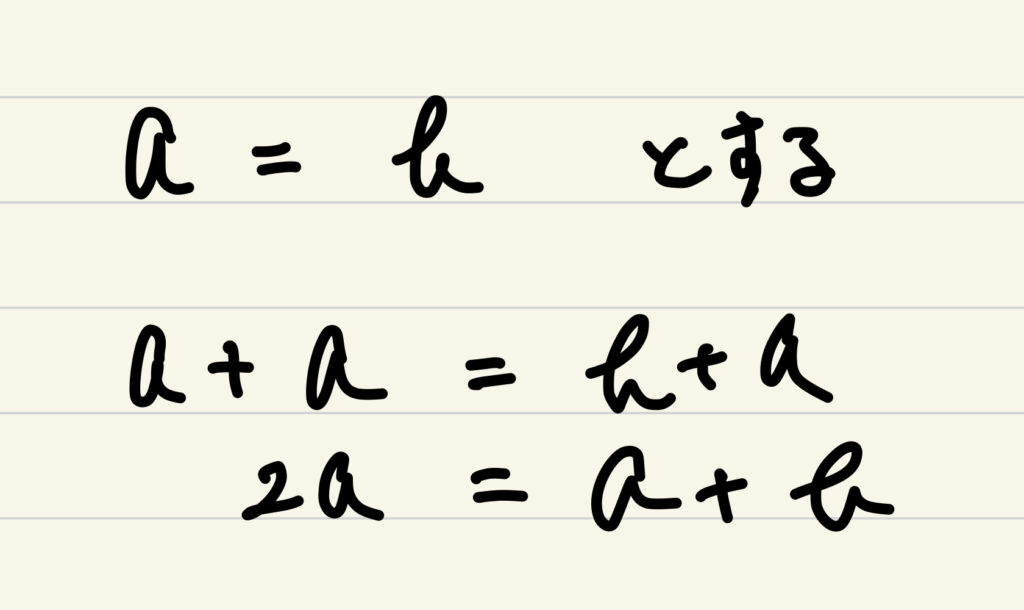
加えて両辺から2bを引くと
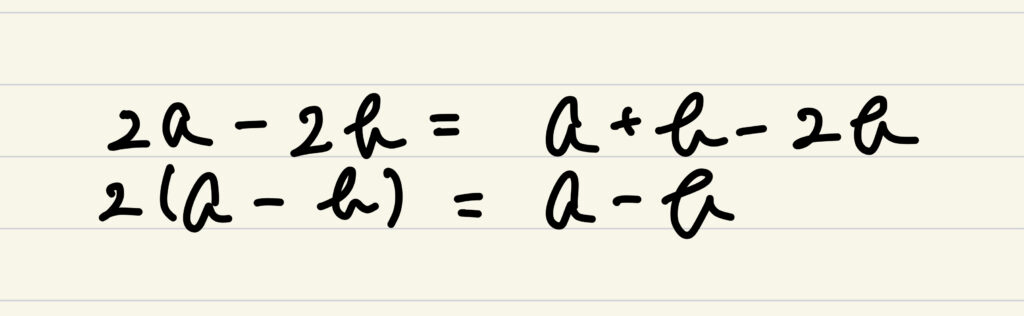
両辺を(a-b)で割ると
2=1になる。
証明②
a=bのとき両辺にaをかけると
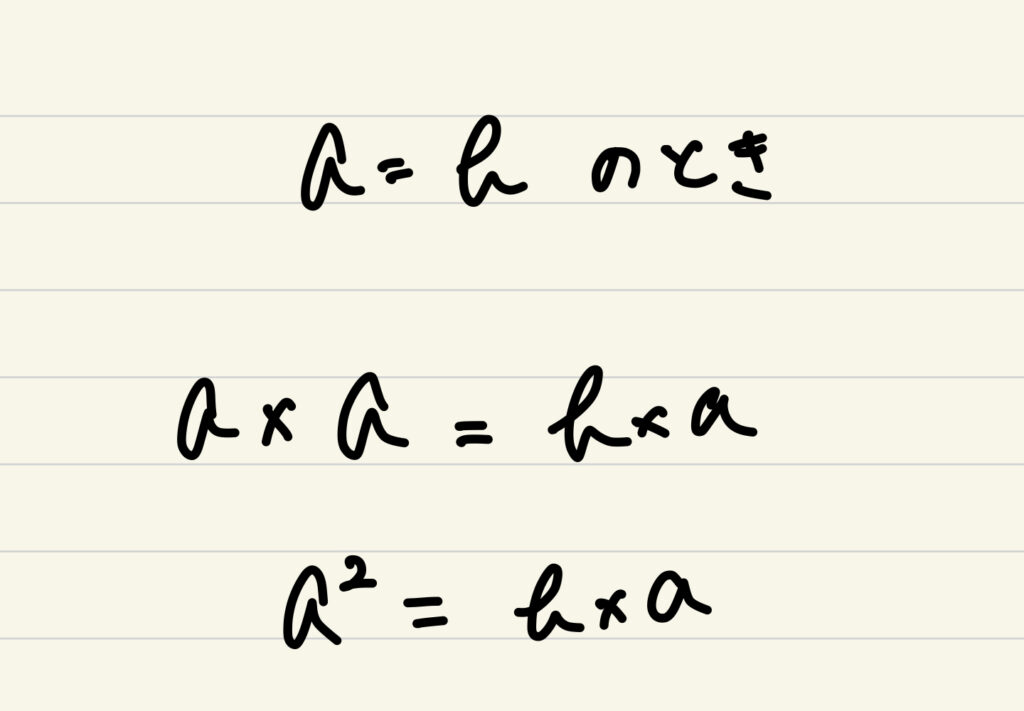
両辺からb^2を引くと
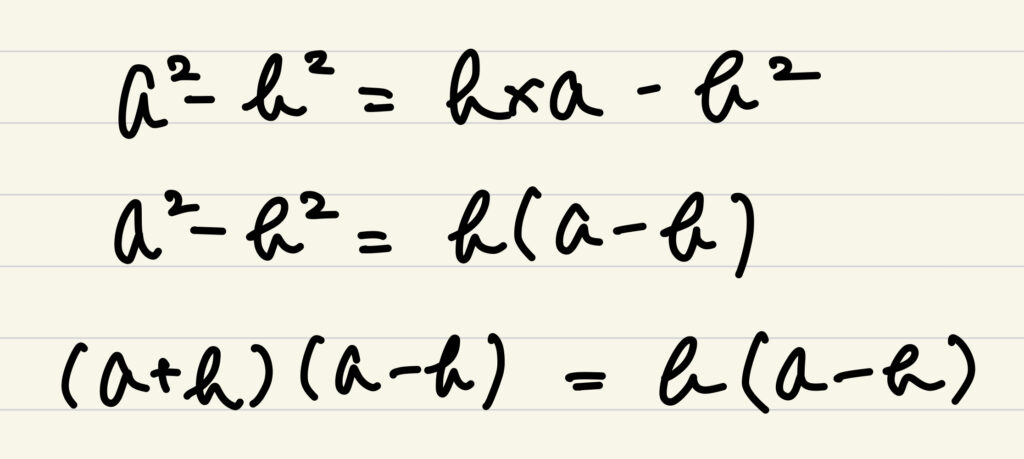
因数分解をしてから両辺を(a-b)で割ると
a=bなのでaにbを代入すると
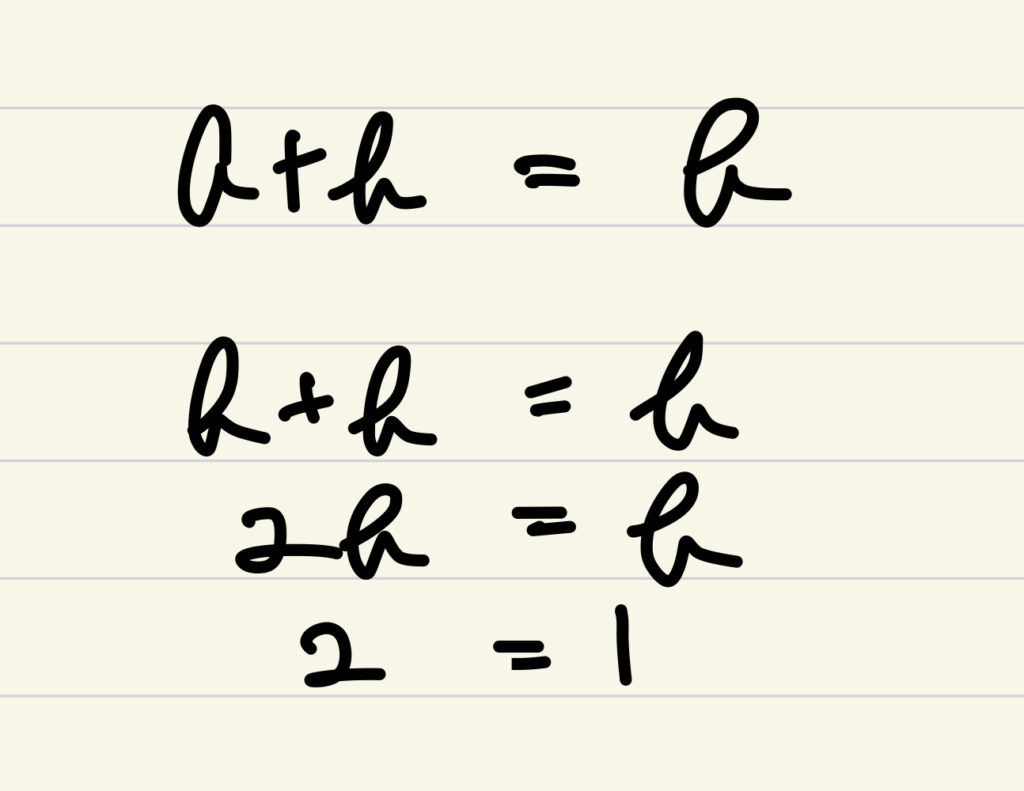
この2つの証明は一見、正しそうですが、実は決定的な間違いがあります。
それは(a-b)で割っているということです。
a=bという前提があるのでa-b=0という意味です。
つまり両辺を0で割っているという事になります。
0で割っては行けないというルールはこういうところから来ていてこのように複数の答えが出てきてしまうので計算ができないとしましょう!とした方が都合が良いのです。
ですから、2=1の証明は間違いなのです。
1=0.9999999999999999……..??
この証明は無限級数の視点での解説は以前に書きましたが、今回は別の証明を行いたいと思います。
1=0.99999999….で
両辺を3で割ると
1/3=0.99999999…/3になるので
0.3333333….=0.333333333…
となり、証明ができる。
これがなぜ成り立つのかというと進法の違いです。
そもそも少数は10進法で1/3は3進法です。
ですので誤差が生まれてしまいます。1/3は循環小数ですがあくまで、10進法にした時無限に続くという事です。
こういった細かなニュアンスの違いも数学の面白いところですよね^^
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
京の算数学 解答#111




