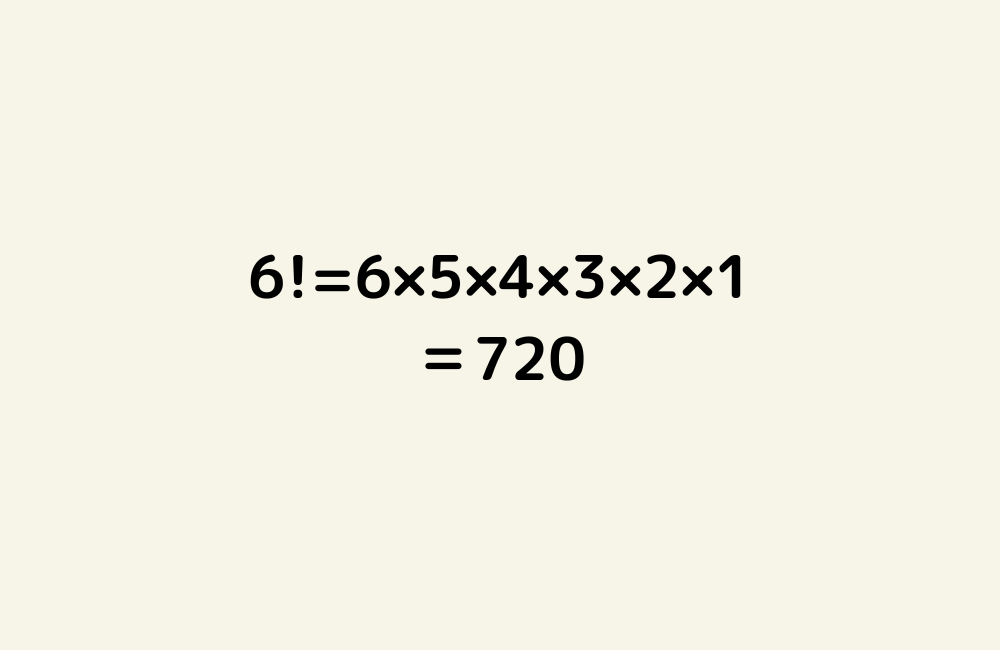数学コラムの目次
京の算数学問題#1093

アイデア数理塾はこちら
算数学コラム
こんにちは!京都市中京区で学習塾「アイデア数理塾」を運営しています、油谷拓哉(ゆたに たくや)です。
今回は、ちょっと不思議な「0の階乗(0!)」についてお話しします。
みなさん、こんな式を見たことはありませんか?
4! = 4×3×2×1 = 24
5! = 5×4×3×2×1 = 120
「!」(びっくりマーク)は「階乗(かいじょう)」と呼ばれ、1からその数までをすべてかけ合わせたものを表します。
でも、ここで問題です。
0!(ゼロの階乗)っていくつでしょう?
答えは……1です。
えっ?0をかけてるのに1?なんだか納得できませんよね。でもこれには、ちゃんと理由があります。
階乗の基本をおさらい!
まずは、階乗とは何かを簡単に復習しておきましょう。
たとえば、
- 3! = 3 × 2 × 1 = 6
- 4! = 4 × 3 × 2 × 1 = 24
- 5! = 5 × 4 × 3 × 2 × 1 = 120
このように、階乗は「その数から1までのすべてをかけたもの」です。
どんどん数が大きくなるので、計算するとかなり大きな数になります。
- 10! = 3,628,800
0の階乗はなぜ「1」になるの?
さて、本題の「0! = 1」についてです。
直感的には、「0って何もないから、全部かけたら0になるんじゃないの?」と思いがちですよね。
でも実は、数学的なルールに従って考えると、0!は1とするのが一番都合がいいんです。
数式で考えてみましょう
数学にはこんなルールがあります。
n! = n × (n – 1)!
たとえば、
- 3! = 3 × 2!
- 2! = 2 × 1!
- 1! = 1 × 0!
ここで注目したいのが「1! = 1 × 0!」という式です。
左辺の1!は「1」とわかっています。では、右辺の「1 × 0!」が1になるためには、0!が1である必要があります。
つまり、この式を成り立たせるために、0!は1と定義されているということなんです。
じゃあ「なぜ定義したの?」という疑問
「それって、なんだか強引じゃない?」と感じた方もいるかもしれません。
でも実は、数学では“都合がいいから”という理由で定義されることも多いんです。
0!を1とすることで、組み合わせ・確率・関数など、たくさんの数学的な公式がスムーズにつながるようになります。
もし0!を1としなければ、たくさんの数式に例外が生まれてしまい、かえって不便なんです。
数学の「強引さ」には理由がある
数学の面白さのひとつは、目に見えないものを扱えることです。
- 0
- マイナスの数
- 虚数
- 無限
- 微分・積分…など
現実には存在しないようなものでも、「定義してしまえば使える」というのが数学の世界。
「それってアリなの?」と思うかもしれませんが、その“強引さ”が数学のすごさでもあるのです。
数学は“哲学”でもある
0! = 1という定義の背景には、数学の哲学的な一面があります。
たとえば、0という数自体も、昔は存在しなかった概念です。
「何もない」ということを“数”として扱うには、大きな思想の転換が必要でした。
実際、0を提唱した学者が宗教的に非難されたこともあります。
それでもある意味では「都合がいいから」という理由で、0や0!、無限などの概念を定義し、今の数学が築かれてきたのです。
まとめ|0!=1は「定義」であり「工夫」
- 階乗とは、1からその数までをすべてかけたもの
- 0! = 1 は、数学をスムーズに成り立たせるための定義
- 一見不思議でも、「都合がいいからこそ」数学の世界ではアリになる
- 数学は現実を超えた「考える力の世界」でもある
0! = 1というのは、不思議に見えて、とてもよく考えられた定義です。
「わからないから面白い」
「意味づけできるから面白い」
そんな数学の奥深さを、ぜひ子どもたちと一緒に楽しんでみてくださいね。
以上、京都市中京区のアイデア数理塾
油谷拓哉(ゆたに たくや)がお届けしました!
算数・数学がもっと好きになるヒント、毎日発信中!
京の算数学 解答#1093