数学コラムの目次
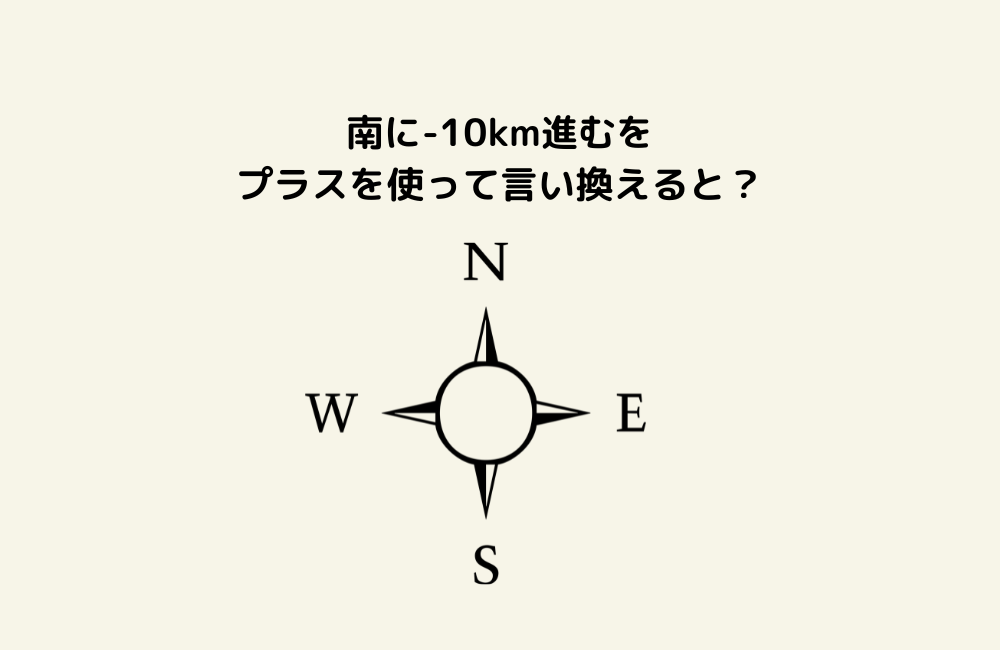
京の算数学問題#808

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
今回は「期待値」についてお話しします。期待値は、確率を含めた平均値の計算であり、特にギャンブルや確率に関連する問題で重要な概念です。具体的な例を用いて期待値の計算方法を見ていきましょう。
期待値とは?
期待値とは、ある動作を行ったときに得られる平均的な結果を確率を含めて計算したものです。
具体的な計算方法を見てみましょう。
期待値の計算例
例えば、サイコロを1回振るゲームを考えます。
出た目に応じて賞金が決まり、次のように設定されているとします。
出た目が1, 2, 3, 4, 5の場合、それぞれの目に応じた賞金は出た目×100円
出た目が6の場合は賞金が0円
それぞれの目が出る確率は1/6です。この場合、期待値は次のように計算します。
期待値 = (100×1/6) + (200×1/6) + (300×1/6) + (400×1/6) + (500×1/6) + (0×1/6)
= 1500/6
= 250
この結果から、このゲームの期待値は250円であるとわかります。
つまり、長期的に見ると1回のゲームで平均的に250円の利益が期待できるということです。
宝くじの基本法則
確率の問題でよく話題に上がるのが宝くじなどの賭け事についてです。
数学的に解析する際、期待値が重要な役割を果たします。
「全ての賭けには期待値がある」と言えます。
期待値を計算することで、その賭けが長期的に利益をもたらすか、損をするかがわかります。
例: 宝くじの期待値
宝くじの期待値を計算してみましょう。
例えば、100円で購入する宝くじがあり、次のような当選確率と賞金が設定されているとします。
1等(5000円)が当たる確率: 1%
2等(200円)が当たる確率: 10%
期待値の計算は次のようになります。
期待値 = (5000×0.01) + (200×0.10) – 100
= 50 + 20 – 100
= -30
この計算から、この宝くじの期待値は-30円であることがわかります。
つまり、長期的には1回の宝くじ購入で平均的に30円の損が出るということです。
確率と面白い確率
確率で物事を考えると、様々な状況やリスクを把握するのに役立ちます。
最後に、いくつかの面白い確率を紹介します。
1/100 初恋の人と結婚する確率
1/2000 ルイス・スアレスに噛まれる確率
1/10000 四葉のクローバーが見つかる確率
1/1000000 雷に打たれる確率
1/7000000 隕石に押し潰される確率
まとめ
期待値を理解することで、日常生活における考え方も確率に基づく決定ができるようになりより決断が明確になります。数値と確率の考え方を使って、物事を科学的に分析する楽しさを感じてみてください。
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#808