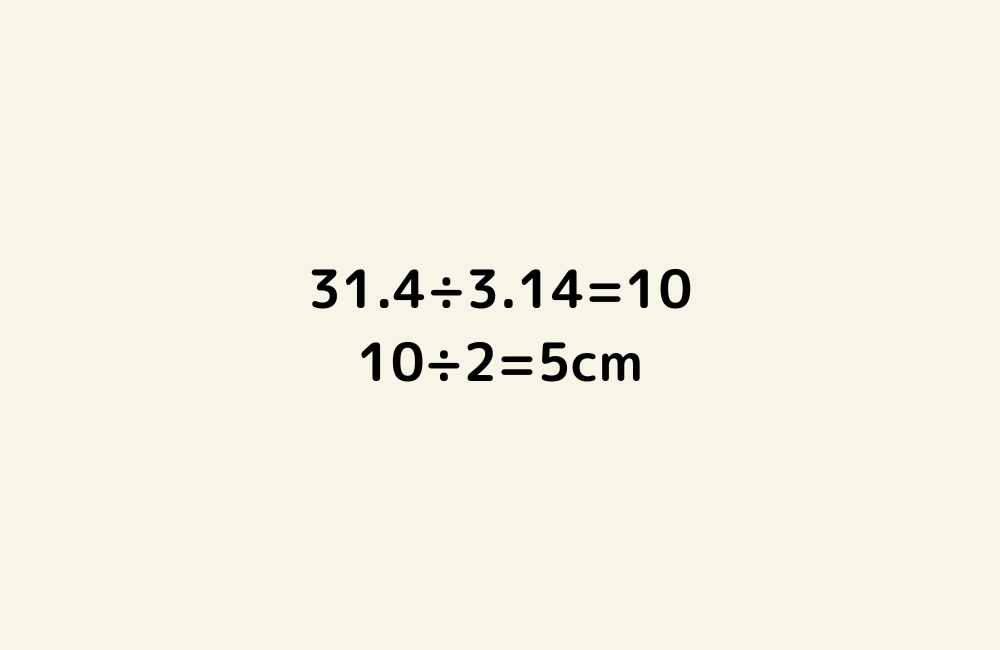数学コラムの目次
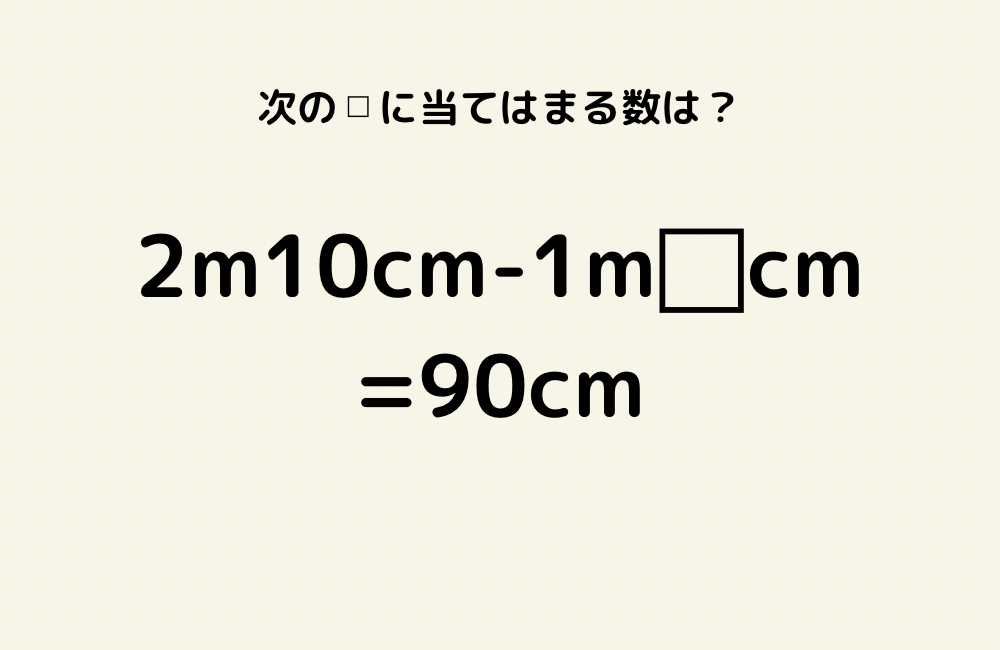
京の算数学問題#795

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
キャッチャーは野球の守備で最も重要なポジションの一つであり、試合全体に対する影響力は絶大です。
キャッチャーの役割は多岐にわたり、ゲームを司るリーダーとして、ピッチャーとのコミュニケーション、戦略の立案、さらには打者との心理戦など、多くの責任を担っています。
今回は、キャッチャーがどれほど重要であるかを数字で見ていきましょう。
セカンド送球の速さと精度
キャッチャーの主な仕事の一つに、盗塁阻止があります。
この時、特に重要なのがセカンド送球の速さと精度です。
キャッチャーがミットに収めたボールをセカンドベースに送球するまでの時間は、プロで平均1.9秒程度とされています。
しかし、これはあくまで平均値です。
驚くべきことに、ソフトバンクの甲斐拓也選手は、そのほとんどの送球で1.7秒から1.8秒の範囲内に収まっています。
この数値は、キャッチャーの送球がいかに素早く、かつ正確であるかを物語っています。
セカンドベースまでの距離は38.795メートルです。
仮にキャッチャーがボールを受け取ってから投げるまでの時間が0.8秒だとすると、残りの38.795メートルをわずか1秒で投げていることになります。
これを時速に換算すると、約140km/hという高速の送球になります。
座った状態から立ち上がり、瞬時にこの速さで投げられる甲斐選手は、まさに「キャノン」と称されるにふさわしい存在です。
盗塁阻止率の重要性
次に注目すべきは、盗塁阻止率です。
これは、盗塁を試みたランナーをどれだけアウトにできたかを示す指標であり、キャッチャーの守備力を測る一つの基準となります。
盗塁阻止率は、盗塁刺(盗塁をアウトにした数)を、盗塁企図数(ランナーが盗塁を試みた回数)で割って求められます。
2021年のプロ野球において、パリーグではソフトバンクの甲斐選手が0.452という高い阻止率を記録し、セリーグでは巨人の大城卓三選手が0.447を記録しました。一般的に、盗塁阻止率が3割から4割であれば優秀とされる中で、これらの数字は非常に高い水準を示しています。さらに、歴代最高の盗塁阻止率を記録したのはヤクルトの古田敦也選手で、その数値は0.462です。このように、盗塁阻止率はキャッチャーの実力を測る上で非常に重要な指標です。
UZR(Ultimate Zone Rating)
キャッチャーの守備力をさらに評価する指標として、UZR(Ultimate Zone Rating)があります。UZRは、同じ守備位置を守る平均的な選手と比べて、どれだけ多くの点数を防いだかを数値化したものです。この指標は、守備力を総合的に評価する際に用いられ、キャッチャーが試合に与える影響力を客観的に示すものです。
2021年のプロ野球において、捕手部門で最も高いUZRを記録したのは巨人の大城卓三選手でした。UZRは非常に複雑な計算によって求められるため、詳細な説明は割愛しますが、この数値が高いほど、キャッチャーとしての守備力が優れていることを意味します。
キャッチャーとしての思い出
私自身、小学校の頃にキャッチャーに憧れ、初めて防具をつけた時のことを思い出します。ショーバン(ワンバウンドする球)を止めようとして何度も失敗し、苦い経験をしました。中学時代には急遽キャッチャーを務めることになり、キャッチャーフライ(高く上がったファウルボール)を取るのに苦労しましたが、その経験を通じてキャッチャーの難しさと重要性を痛感しました。
キャッチャーは単に球を受けるだけでなく、ピッチャーとコミュニケーションを取り、相手チームに対抗するための戦略を立てる役割も担っています。中学2年生の1年間、キャッチャーとしてチームを支えた経験は、私にとって非常に貴重なものでした。この時の経験が、後に大学でピッチャーを務める際に、他の選手とは異なる視点でゲームを考えるきっかけとなりました。
まとめ
キャッチャーは、表には出にくいながらも、試合全体に大きな影響を与える重要なポジションです。セカンド送球の速さ、盗塁阻止率、UZRといった数字からも分かるように、キャッチャーの技術と判断力はチームの勝敗を左右する要素となります。私自身、キャッチャーとしての経験を通じて、野球の奥深さを学びました。数字を使って具体的に戦略を考えることの重要性を実感した今、キャッチャーというポジションがいかに奥が深く、魅力的であるかを改めて感じています。
キャッチャーの役割は、守備の範疇を超えて、チーム全体の戦略を練り上げるリーダーシップが求められます。このポジションの面白さと奥深さは数字で表すとよくわかります。
まさにデータ野球ですね。
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#795