アイデア数理塾 京の算数学問題#792
算数学コラム
みなさんこんにちは！京都市中京区で塾を運営しております。油谷拓哉（ゆたに たくや）です！
中学生になると「方程式」を学びます。
例えば、`x + 3 = 4` という問題を解く際、`x = 1` と簡単に答えを出すことができますが、重要なのは「移項」の本質を理解することです。
方程式とは？
方程式は「=」でつながれた等式に未知数xが存在した時に、xがある特定の数字をとる場合にのみ成立するものを言います。
方程式で大切なのは左辺と右辺の数が同じであると言うことです。
移項の理解
「移項」は、方程式を解く際に、一方の辺に変数（x）を集め、もう一方に数字を集める操作です。
よく「符号を変えて移動させる」と教えられますが、実際には等式の両辺に同じ操作を行った結果として項が移動したように“見える”だけです。
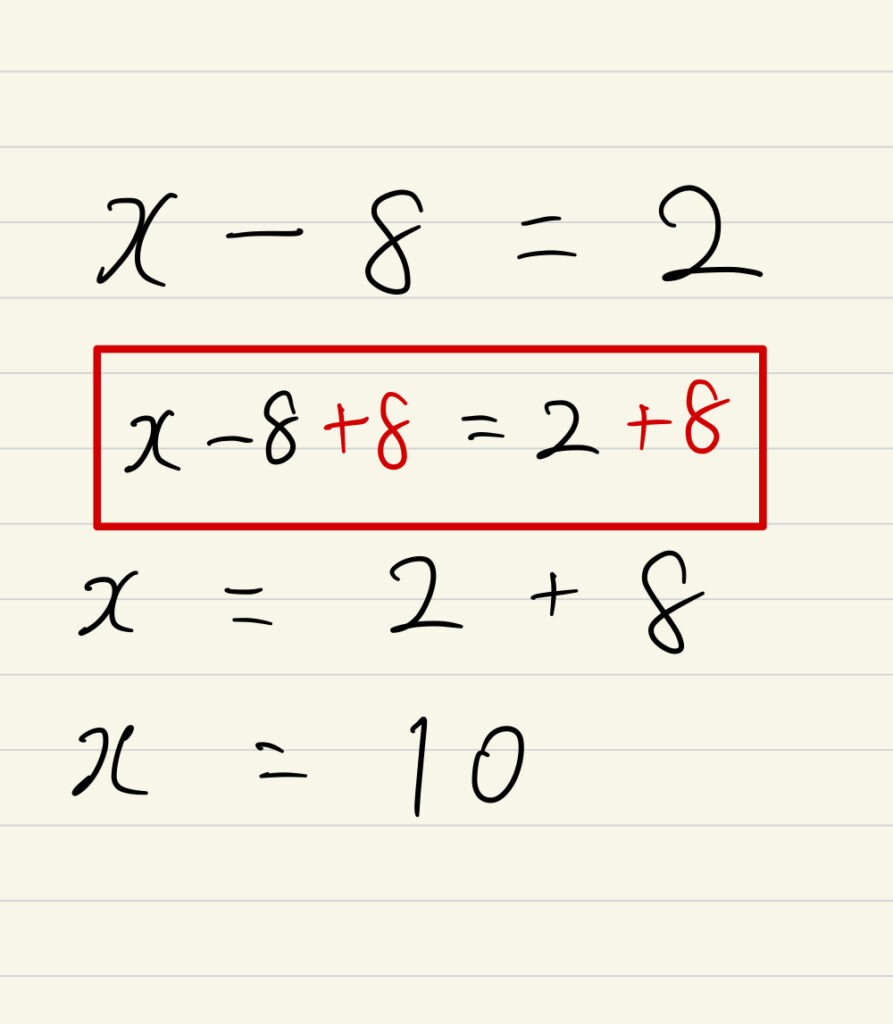
応用と理解の深化
この原理をきちんと理解すれば、分数や複雑な文字式の計算でも応用が可能です。
例えば、分数を無くすために全体に掛け算をし、計算を簡単にしてから解答を求める方法もあります。
このような方法は、本質を理解しているからこそ可能です。
方程式を学ぶ意義
方程式を学ぶことで、計算の正確性が上がり、応用問題にも対応できるようになります。
数学の学習は、ただ答えを出すだけでなく、その過程を深く理解し、自分に合った解き方を見つけることが大切です。
中学受験でよく用いられる特殊算も実は方程式を使えば簡単に解けてしまうのです。
方程式の本質を理解し、自分なりの解法を見つけていきましょう！
以上！京都市中京区のアイデア数理塾 油谷拓哉（ゆたに たくや）がお届けいたしました！
算数好きあつまれ〜！
京の算数学 解答#792
