京の算数学問題#662

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
高校2年時に履修する数学Ⅱの範囲で学ぶ複素数という単元ですが、今まで実数しか知らない私たちにとっては新しい概念でもありなかなかイメージをつける事ができません。
今日は複素数の単元の導入部分をわかりやすくお伝えしていきます。
虚数ってなに??
虚数とはImaginary number と言い、想像上の数という意味です。
アルファベットのiで表し、iの2乗=–1と定義します。
解の公式をイメージしましょう。
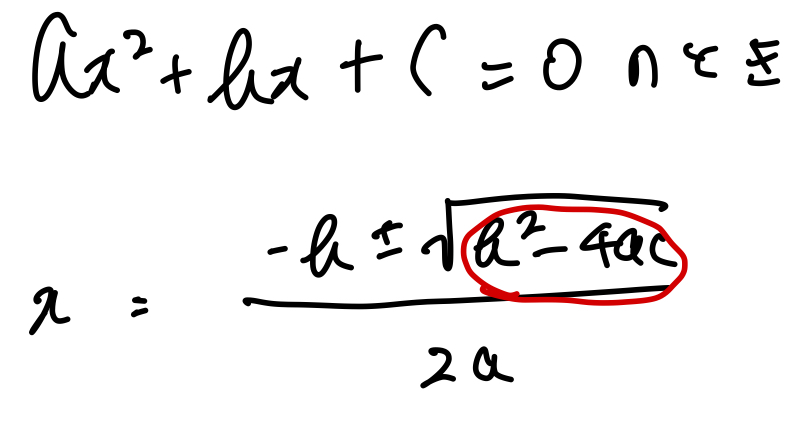
この時私たちが今まで解いてきたのはルートの中(判別式)が0以上の時でした。
ですが、計算をしているとマイナスの場合も多々出てきます。
その計算を可能にしたのが虚数です。
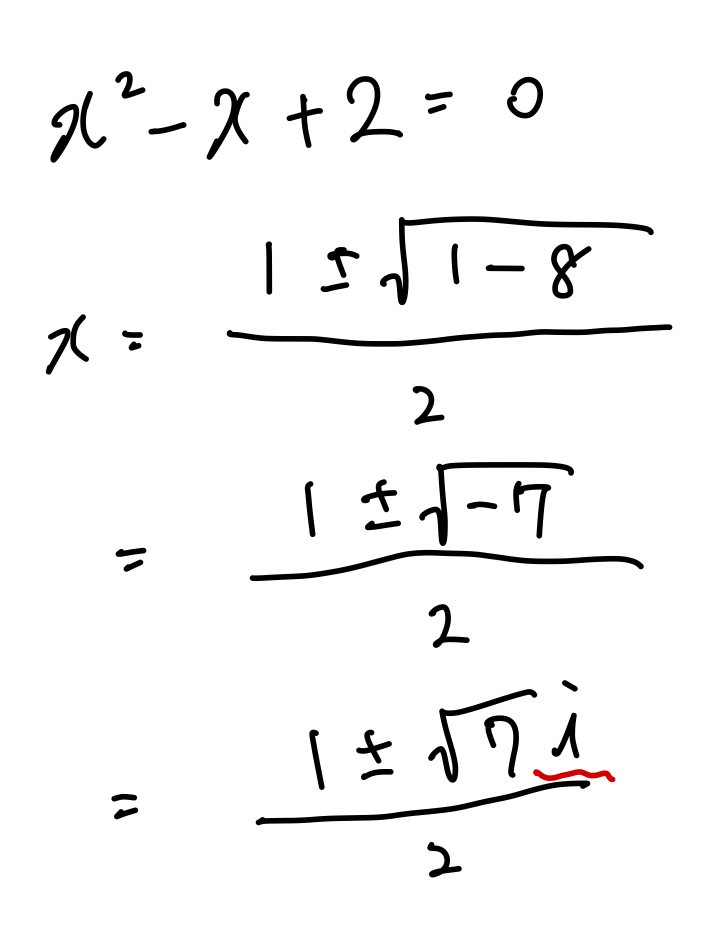
このように通常では計算できない2次方程式も計算する事ができるようになります。
この虚数という世界の広がりによって様々な発展が可能になったとされています。
・複素数と虚数の違い
単元名が複素数ですから、よくiが複素数だと混同されがちです。
複素数とはai+bで表され、虚数の部分を虚部、実数の部分を実部と表します。
この虚部と実部で表されるものを複素数と定義しています。
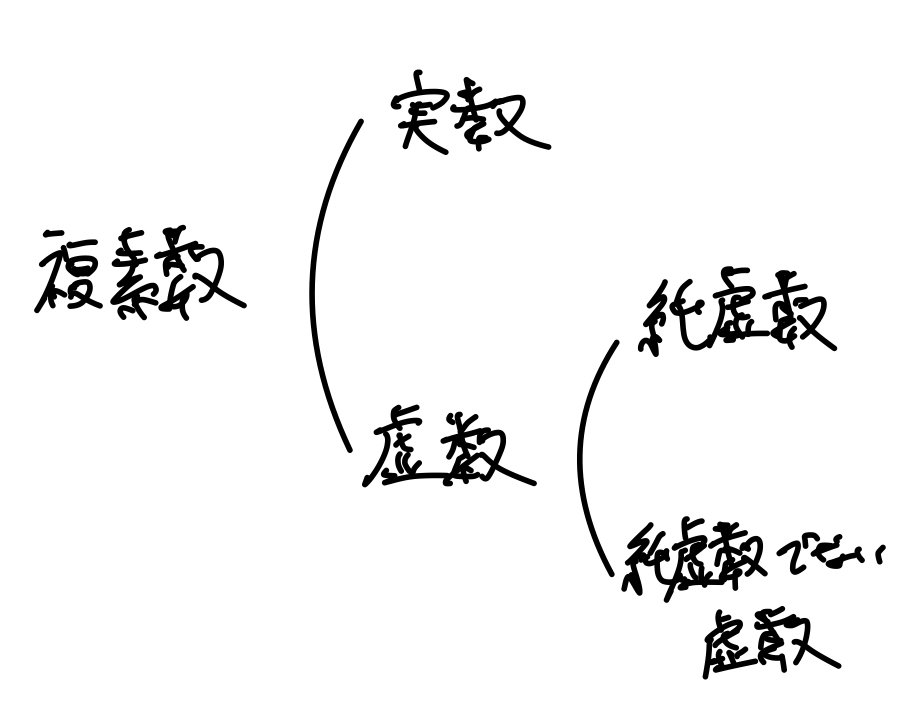
虚数は純虚数(iや4iなど虚部だけの複素数)と純虚数ではない虚数(1+3iなど)に分かれます。
共役の複素数って何?
a+2iに対し虚数に−をかけたものa-2iを共役の複素数と言います。
共役とは互いに補う関わりをするものという意味があります。
つまりこの共役複素数において、
和を求めると(a+2i)+(a-2i)=2aとなり
積を求めると(a+2i)(a-2i)=a^2+4となりいずれも虚部が無くなります。
特に複素数の割り算では平方根でいうところの有理化のような作業があり共役の複素数は複素数の割り算で大活躍をします。
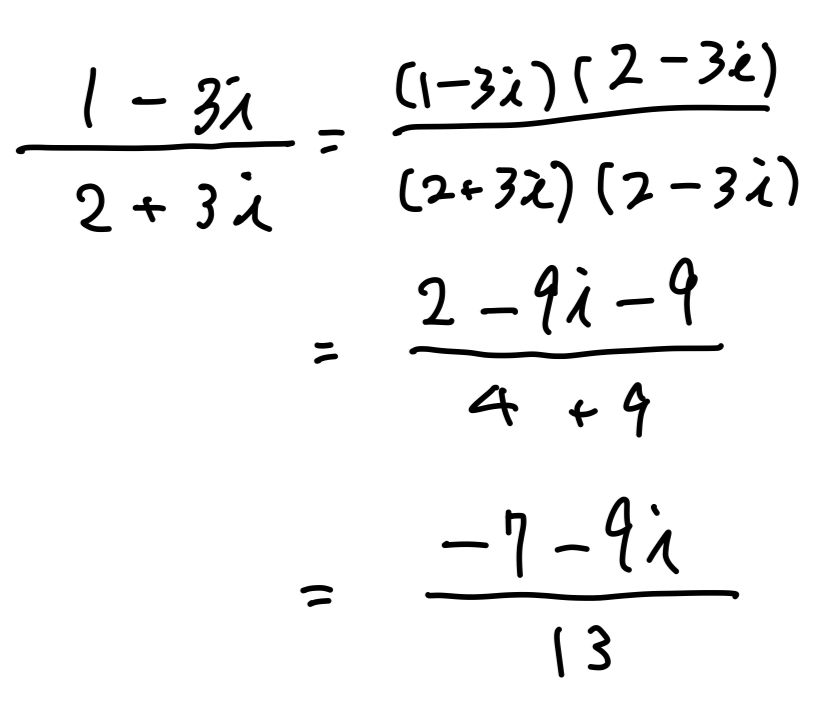
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#662




