数学コラムの目次
京の算数学問題#449

算数学コラム
みなさんこんにちは!京都市中京区で学習塾を運営しております。油谷拓哉(ゆたに たくや)です!
分数で割るとなんでひっくりがえるの?!
とある小学生が言いました。
確かにごもっとも。
そういうものとして扱ってしまえば楽なんですが子どもたちの好奇心を刺激するために今日は油谷先生頑張っちゃいます。
疑問を持つことはいいこと!ということで解説していきます^^
イメージしづらい分数の世界
今まで1、2、3などイメージがしやすかった数字ですが、小学3年生からは徐々に数字の世界が広がっていきます。
それが小数と分数です。
これに関してはリアルに示すことが難しくなかなか教えるのに苦労します。
そして今回の主題である分数のわり算はなぜひっくり返るのか?!につながるわけです。
※ちなみに分数のわり算がひっくり返ることを逆数をとると言います。
わり算の性質で考えてみよう!
わり算は割られる数と割る数に同じ数をかけても答えは変わらないという性質があります。
例えば、18÷2=36÷4=54÷6=9です。
そこでこんなふうに考えてみました。

割る数を1にすれば万事解決です!
だから性質上分数のわり算はひっくりがえるのです。
かけ算に直して考えてみる
例えば18÷2=◻︎をかけ算に直すと
2×◻︎=18となります。
つまり2×9=18となりますので◻︎=9だという事がわかります。
分数の場合も考えてみましょう。
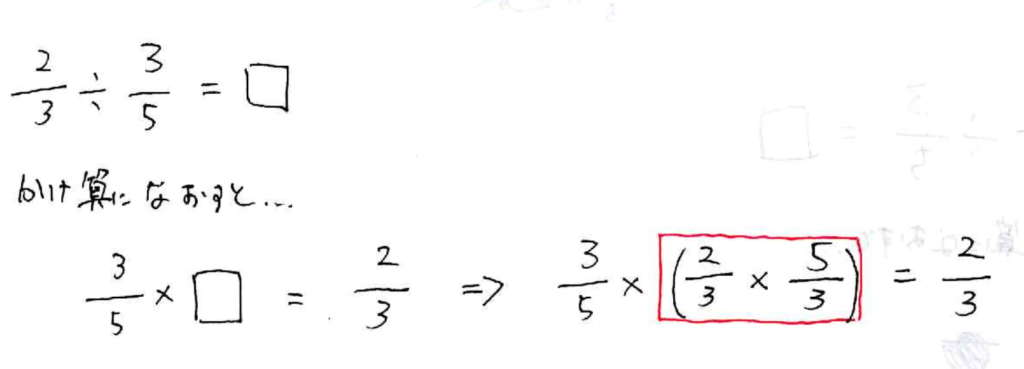
これだと結果的に分数がひっくり返ったでしょ!
イメージで解いてみる
今までは式の性質を使った解き方ですが、実際に納得するかと言われれば怪しいですよね。
そこでこんなイメージをしてみましょう。
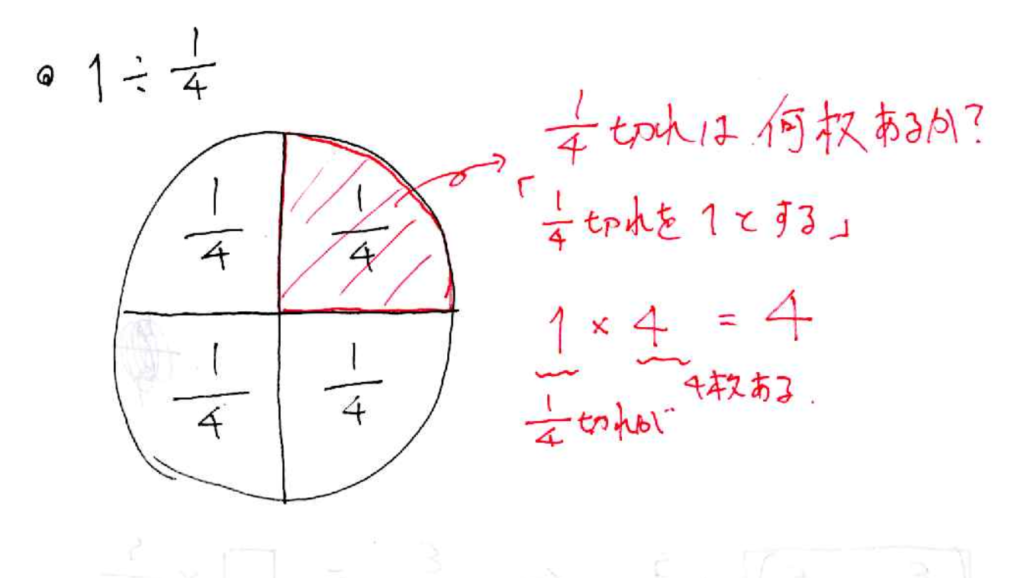
割り算において割る数は単位量といえます。
例えばガソリン40Lで400Km走る車がある時、ガソリン1Lで何km走れるか?を考えると、
400km÷40L=10kmとなります。
同様に分数のわり算も割る数である4分の1を1とすると4分の1切れは4枚あるということになります。
このように図形を使ってイメージをするとわかりやすいですよね!
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#449