数学コラムの目次
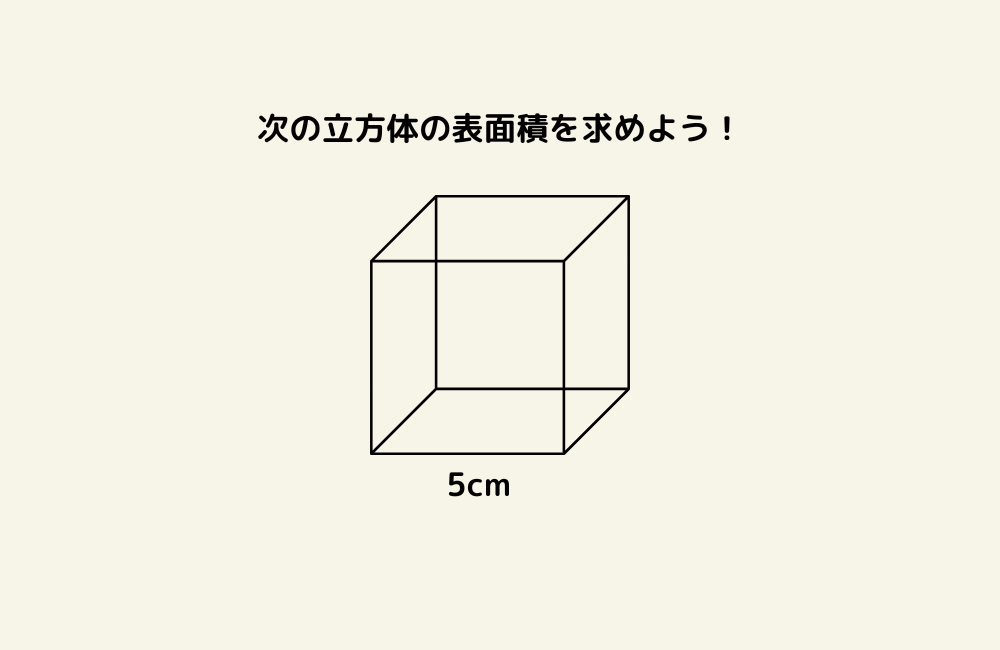
今日の数学問題#372
数学コラム
みなさんこんにちは!京都市中京区で学習塾を運営しております。ゆたに たくやです!
今日は中学生、高校生の生徒から良く質問のある数学の応用力の付け方についてについて解説をしていきます!
応用力を身につけたい方必見でございます!
応用力ってそもそも何?
応用力とは基礎をうまく活用することで成り立つ力のことです。
重要なのは応用力をつけるために基礎力は必要不可欠だが、基礎力をいくらつけても応用力がつくとは限らないと言うことです。
応用力とは基礎力として身についている知識や定理を活用し対象の問題を解くために必要なものだけを組み合わせる力のことです。
すごく簡単に言うと国語で言う読解力なんです。
数学の応用はある程度の妥協が必要!
数学の定理にはなぜそうなるのか?が説明できるものととりあえずこう言うものだと割り切って覚えてしまう方が良いものがあります。
例えば0乗がなぜ1になるか?というのは証明というよりもそうした方が都合がいいからもう0乗=1としましょう!という力技の定理です。これをなぜ?と考えても仕方ありませんのでそういうものだとして割り切りましょう。
0乗を1だとしたおかげで多くの定理がすんなり成り立つようになりました。
数学の応用力をつけるための学習法
定理の証明をしよう!
まずは数学には定理が多いです。それぞれの定理には成り立ちのプロセスがあり、教科書にはそれが書いてあります。
教科書を中心に定理の成り立ちや証明、理屈を理解しましょう!
なぜそうなるのか?を理解すれば定理を数式として見るのではなくどう使えば良いのか?が明確になります。
例えば三角形の面積の求め方でも底辺×高さ÷2です。
これは平行四辺形の半分だから底辺×高さなんですね。
ここから平行四辺形と三角形の関連性がわかります。
問題集の解答にツッコミを入れよう!
問題の解答集には難易度にもよりますが、さもわかって当然かの如く解答解説が描かれていますが、読んでもわからないところがありますよね。
そこをどんどん突っ込んでいきます。
例えば式の変形1つ取ってもなぜそこでこう言う変形をしたのか?
何の定理を使っているのか?
なぜその定理が必要だったのか?
定理を使用した意図は?
など解答解説にツッコンでいき、メモを解説に注釈していきましょう!
解答をメモだらけにしてしまいましょう!
その問題の解き方を2分で説明してみよう!
問題を解き終わったら注意すべきはわかった気になることです。
良くあるのですが難しい問題が途中までできて解説を読んで納得した。
でも本番できなかった。これは理解する前に納得したところで満足をしてしまったから怒るミスです。
理解できると言うことは説明できると言うことなので、1人言でも良いので今解いた問題の解き方を2分以内に簡単に解説できるようになっているか?に取り組んでみましょう。
例えば空間図形の問題ならまず底面積を求めたいから高さを三平方の定理で求めると低面積が求められる。それに高さをかけて錐だから3で割ると体積が求められると言うような感じです。
数学の応用力は基礎がある前提ですが、基礎だけをやり続ければつくわけではありません。
基礎を知っているで終わらせないためにぜひ挑戦してほしい学習法です^^
以上!京都市中京区のアイデア数理塾 ゆたに たくやがお届けいたしました!
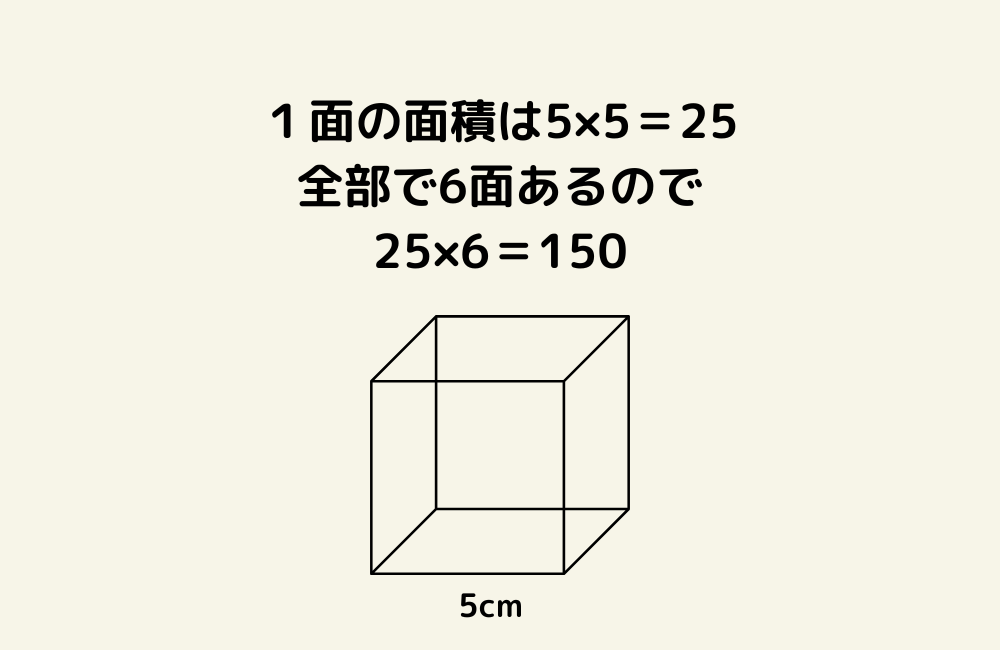
今日の数学 解答#372