アイデア数理塾 京の算数学問題#337
数学学コラム
小学5年生で学ぶ最小公倍数と最大公約数。
分数を学ぶのに必要不可欠な単元なのですが結構つまづく生徒が多い印象なんです。
でもご安心ください！
最小公倍数ってコツがわかるとすごく簡単なんです！
今日は最小公倍数の解き方を３つの方法で学んでいきます。
最小公倍数ってなに？
最小公倍数とは最小の公倍数という意味です。
例えば
3という数字があったとします。
3×1＝3
3×2＝6
3×3＝9 など
3,6,9,12,15,18,21…….というような「ある１つの整数を何倍かした数」を倍数と言います。
2の場合
2,4,6,8,10,12,14,16,18…….
となりますが、3と2の倍数を比べると、6,12,18のように共通の倍数がみられます。
このように「２つ以上の整数に共通な倍数」を公倍数と言います。
このうち最も小さな倍数（3と2の場合は6）の事を最小公倍数と言います。
実際に最小公倍数の問題を解いてみよう！
【問題】
次の最小公倍数を求めよう！
（６と21）
大きい方の数の倍数から考える
まずは21の倍数を書いていきます。
21,42,63,84,105….
その中から6の倍数を探していきます。
この場合42,84などがそうですね。
よって最小公倍数は42となります。
このように大きい数から考えるというやり方はたとえ３つの整数の最小公倍数でも有効になります。
筆算を使って求める
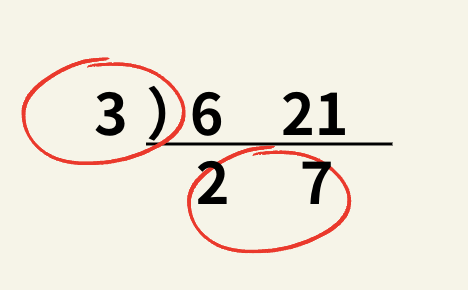
そしてこの左と下の丸の付いている部分を掛け合わせると３×２×７＝４２と最小公倍数が求められます。
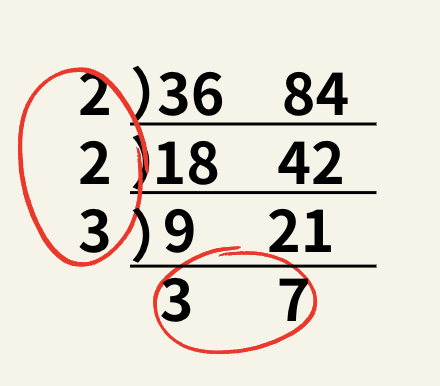
この筆算の方法自体は求めたい倍数を横に並べ共通の割れる数で割れなくなるまで割っていきます。
この方法だと例えばもっと数が多くなっても、１つずつ倍数を出すよりもかなり簡単に解くことができます。
その際に何で割れるか？はポイントとして覚えておきましょう。
2で割れる＝一の位が偶数
3で割れる＝各位を足して三の倍数
５で割れる＝一の位が５か０
この辺りは覚えておくと便利です。
素因数分解で求める（中学生向け）
中学生で学ぶ素因数分解は、整数を素数の組み合わせで表すことのできる便利な物です。
この場合だと
21＝3×7
6=2×3
と表すことができます。
最小公倍数は「各素数の指数が最大の数字をかけた数」なので
2×3×7＝42となります。
このやり方は中学生になった時に深く勉強をしていきます。
いわば筆算でのやり方の根本的な解説に当たりますのでこのブログをお読みの小学生の皆様はまず１つ目のやり方をマスターしてから２つ目の筆算にトライしてみましょう！
以上！京都市中京区のアイデア数理塾 油谷がお届けいたしました！
京の算数学 解答#337
