今日の数学問題#263

数学コラム
グラフの導入として学ぶ『座標』
中学1年生で本格的に学ぶ単元ですが、特に迷うのが対象をとる時です。
え?!x軸に対象?!
原点に対象?!
線対象?!
わからない!!
この単元はつまづく時はめっちゃつまづきます。
今日は誰でも簡単にできるように座標平面を掘り下げてお話ししていきたいと思います。
線は点のあつまり
まず初めに座標とはそもそも何なのか?
よくグラフというと直線や曲線が描かれますが、この線は小さな点の集まりでできています。その点を座標と言います。
つまり座標の集合体がグラフということです。
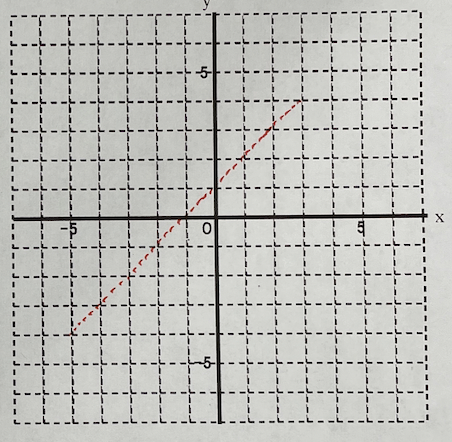
点をつめつめでノートに書いてみてください、遠くからノートを見ると線や平面など繋がっているように見えますよね。
座標は超シンプルな地図
では座標のメリットは何かというと、超シンプルな地図ができるということです。
一般的な地図は上側を北とし、方角と通り名などによって住所が決まり目的地と現在地がわかります。
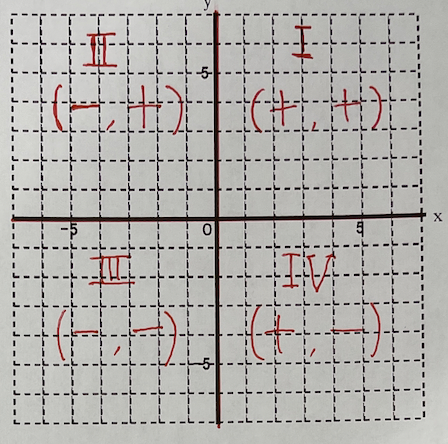
地図で言う郵便番号のようなものが第○象限と言い、第Ⅰ〜Ⅳまであります。
第Ⅰ象限は、(+,+)xもyもプラスの位置にある場所です。
第Ⅱ象限は、(―,+)xがマイナスyがプラスの位置にある場所です。
第Ⅲ象限は、(―,―)xもyもマイナスの位置にある場所です。
第Ⅳ象限は、(+,―)xがプラスyがマイナスの位置にある場所です。
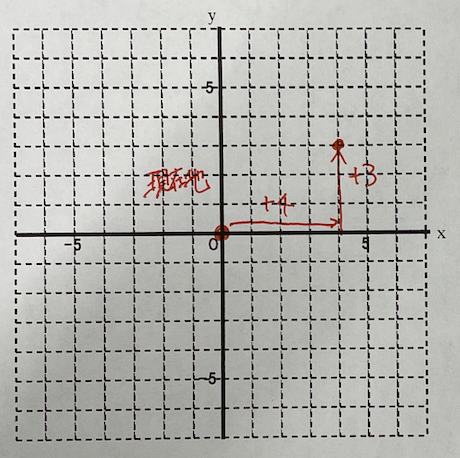
そして次に住所と番地です。
(4,3)と書き、この場合はx方向に4、y方向に3進めば目的地に辿り着くよと言う意味になります。
座標のすごいところは今いる現在地を原点0とした時にどっちの方向へどれだけ進むかだけがわかるのです。
対象の考え方
対象とは対になるものです。
わかりやすく言えば、紙を折った時に重なる点です。
【問題】
次の座標をそれぞれ求めよう。
A(3,4)について
・x軸対象に移動した点B
・y軸対象に移動した点C
・原点対象に移動した点D
X軸対象の場合
X軸対象とはx軸について対象=x軸に沿って折りましょうと言う意味です。
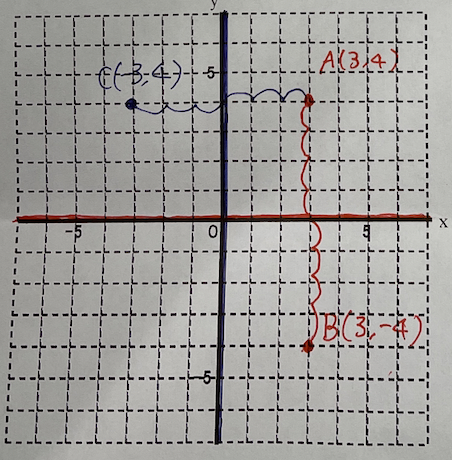
例えば画像だとA(3,4)をx軸対象とする場合、x軸で折って重なる点の座標を求めます。
つまり、点Aからx軸は4離れているのでx軸から点Bまでも4離れていることになります。よって求める点B(3,-4)
y軸対象の場合
y軸対象とはy軸について対象=y軸に沿って折りましょうと言う意味です。
例えば画像だとA(3,4)をy軸対象とする場合、y軸で折って重なる点の座標を求めます。
つまり、点Aからy軸は3離れているのでy軸から点Cまでも3離れていることになります。よって求める点C(-3,4)
原点対象の場合
原点対象も基本は同じで原点に沿って斜めに折ります。
原点から点Aまではx軸方向に3進みy軸方向に4進めば辿り着くことができますので、原点から点Dまでも同様にx軸方向に-3,y軸方向に-4進むと求める点D(-3,-4)となります。
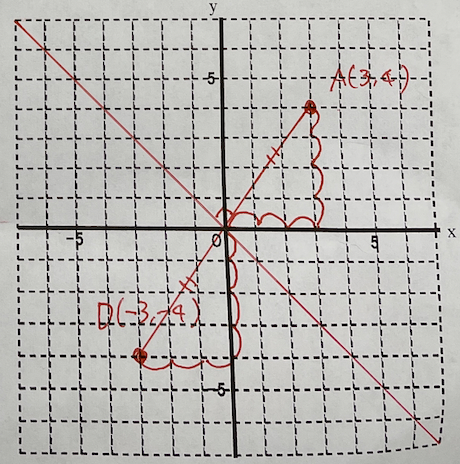
実際にグラフを紙に書いて折ってみるとイメージしやすいですよ^^
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
今日の数学解答#263



