数学コラムの目次
京の算数学問題#191

京の算数学コラム
連立方程式は中学2年生で初めて学びますよね。
ちょうど夏休み前後で学ぶことが多いです。
学んだ当初は文字が2つあるだけでこんなに難しいのか?!と思う事もあると思いますが、実はこの連立方程式は高校に入ってからその力を発揮します。
1年生で学んだ方程式の進化系とも言える連立方程式は高校でさらに進化をしていくのです。
以前は3つの文字を連立させて解きましたが今回は旧過程数学Cの行列の範囲です。
行列とは?
行列は新課程で数学Cに再登場した単元です。
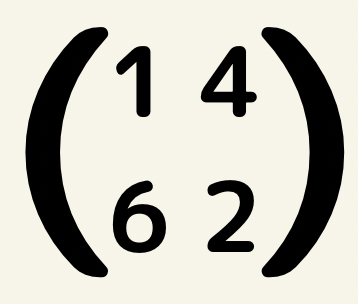
これを2×2の行列と言います。
行列をしっかり学ぶと複雑な連立方程式も最も簡単に解くことが出来ます。
連立方程式を行列で解いてみた
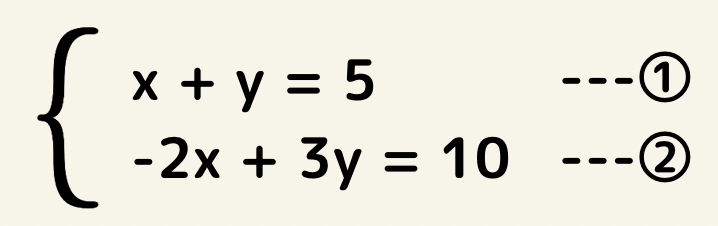
この連立方程式の場合行列式で表すと、
行列の積の法則を用いると
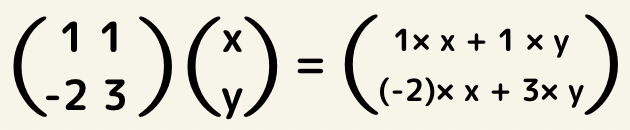
となるので、元の連立方程式と同じになる事がわかります。
また、行列式は簡略化して書くことが出来ます。
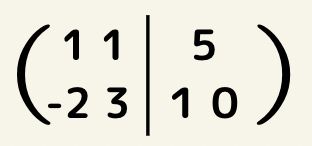
そしてこの行列式を使って連立方程式を解いていくのですが、
行列式を変換していくと解を導き出す事が出来ます。
連立方程式の通常の解き方では、①の式を2倍し②の式と足す事でxの文字が消えましたね。
つまり、行列式も同じようにまず①の式(上の列)を2倍し②の式(下の列)と足します。
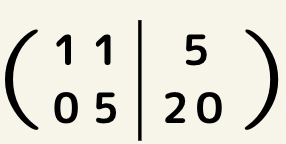
次に②の式(下の式)を5で割ります。
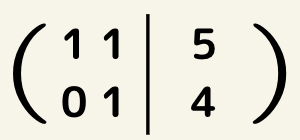
これでyの値が求まりました。
次に、①の式(上の式)から②の式(下の式)を引くと
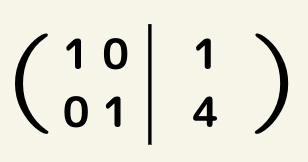
このように対角線で1と0が並ぶ(単位行列)にすることが出来ます。
これを元に戻すと、
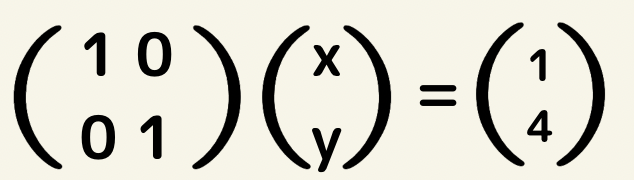
このようになり、x=1,y=4と求める事が出来ます!
この行列式が真価を発揮するのはもっと複雑な連立方程式の場合です。
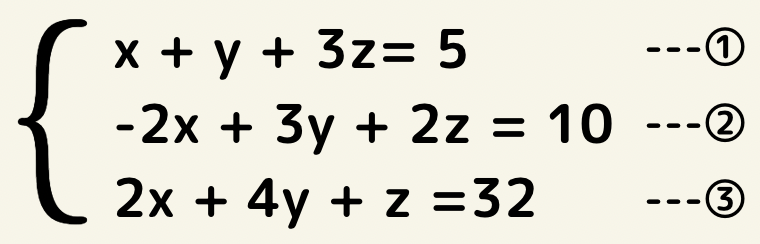
行列式に直すと
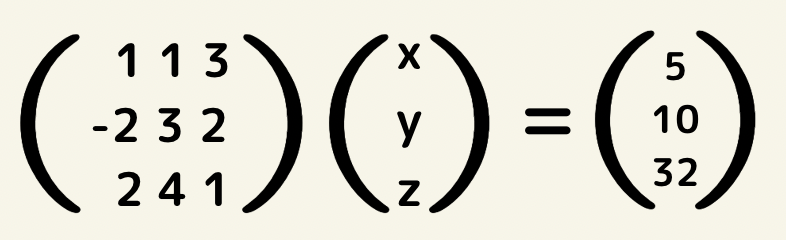
同様に簡略化すると
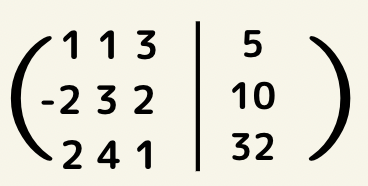
このような3×3の行列になります。
この場合も対角に1を作っていきます。
まず左下から0を作っていきます。(掃き出し法)
①の式×2+②の式をすると
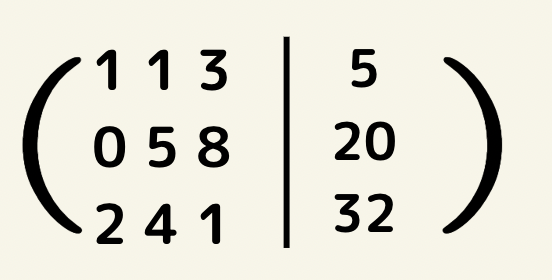
途中計算は長くなるので省略するが、計算を進めると
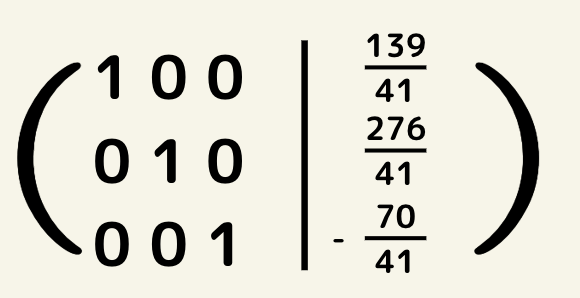
このようにx,y,zそれぞれの値を求める事が出来る。
行列の復活が検討されているわけ
学習指導要領の改定による1番の注目ポイントは「統計分野」です。
統計は政府のAI戦略の中心であり、プログラミング思考などとも関連性がある。
行列は統計分野や確率分野とも関連性が強い単元です。
ですので、行列の復活は良く議題に上がるのですが、なかなか実装には至っていません。
私は2010年卒でしたが、2012年から行列を学ばなくなりました。
行列はベクトルとの関連性も強くなぜ復活しないのか?は個人的にも疑問が残るところです。
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#191



