数学コラムの目次
京の算数学問題#190

京の算数学コラム
連立方程式は方程式に比べて計算が複雑と感じていませんか?
確かに文字が2つに増えたことによって視覚的な難しさを感じることもあるかもしれません。ですがこれもパターンです。
今日のブログはいろいろな連立方程式の解法パターンを4つのポイントで解説していきます。これであなたも連立方程式マスターだ!
Point1 まずは、加減法と代入法を両方マスターしよう!
まずは連立方程式は加減法と代入法がありました。
加減法、代入法の詳しい解法は下記のおすすめの数学ブログをご覧ください。

大きくはこのように判別して良いです。
特に中学数学では解法を指定される事が多いのでどちらも使えるようにしておきましょう!
Point2 解答の書き方をマスターしよう!
解答の書き方は定型文として覚えておきましょう。
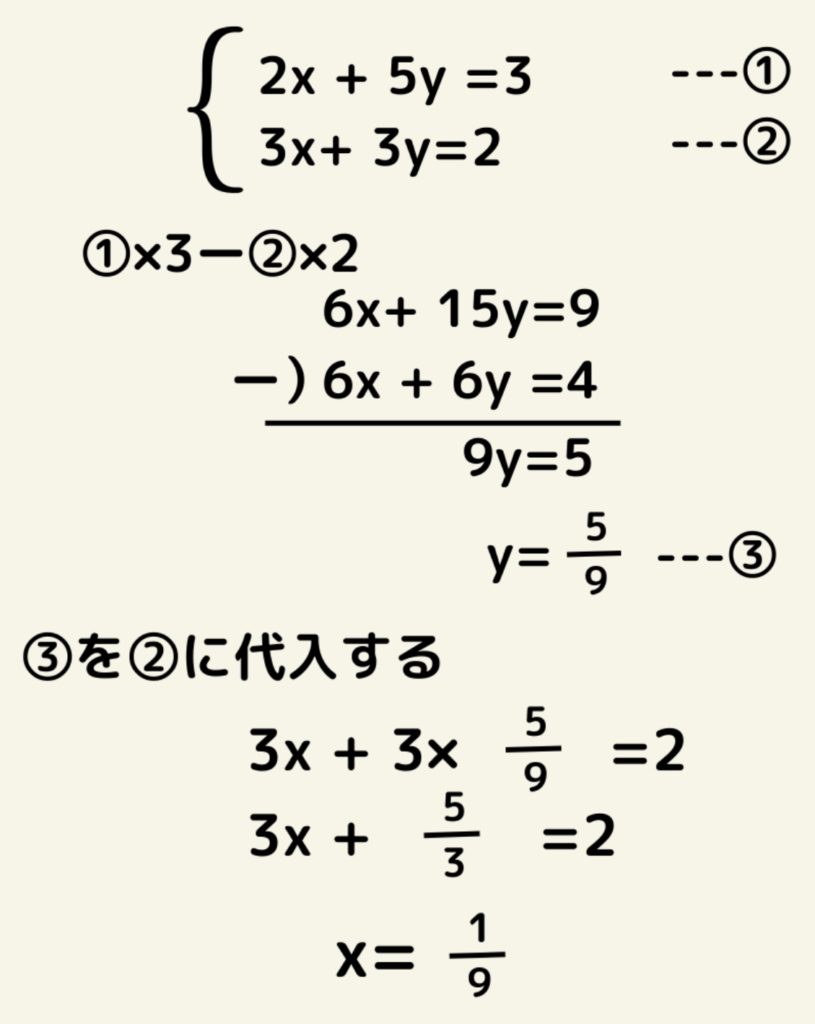
このように、
式に番号を割り振った後、加減法か代入法を決めて解答の流れを記載します。
ここでの記述の注意は簡略化しない事です。
くどいようですが、記述の目的は「採点者にわかる解答を書く事」が一番です。
採点者がわかるという事は誰が読んでもわかる文章や記述が望ましいですよね。
そのためにこの定型文を学びます。
違和感があってもまずは書き方を丁寧にして解いていきましょう!
Point3 解法パターンの定型を覚えてしまおう!
解法パターンは大きく分けて解説をしていきます。
・係数が揃っているパターン
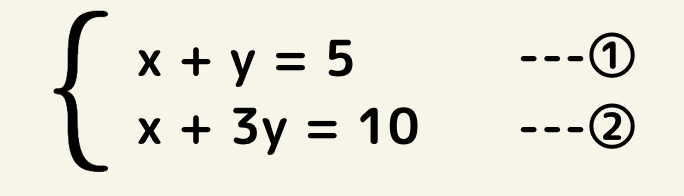
この場合は迷わず一方の式からもう一方を引きます。
②-①をすれば、2y=5 y=5/2とすぐに解答が出てきます。
あとはこれを①に代入するだけです。
・係数がバラバラのパターン
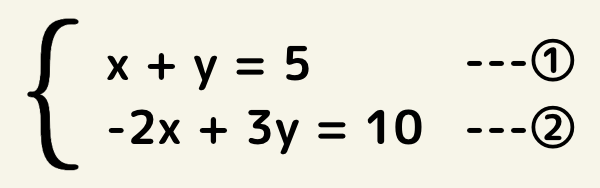
この場合はxかyどちらかの係数を揃える必要があります。
つまり、①×2をした式から②を加えるとxが消えます。
5y = 20 y=4とyの値が求まりました。
あとは同様に①に代入をしましょう。
・y=やx=などのパターン
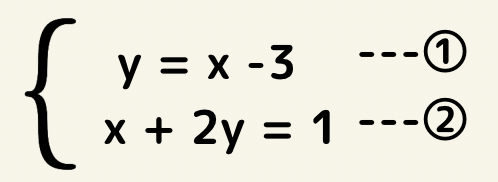
この場合は、②の式に①の式を代入します。
x + 2(x – 3) = 1 となるので x = 7/3 となりあとは同じです。
Point 4 いろんな連立方程式を解くコツ
連立方程式の終盤は分数や少数、カッコがついたパターンなど複雑な計算パターンが出てきますが基本的には今までのPoint1〜3を理解していれば解くことが出来ます!
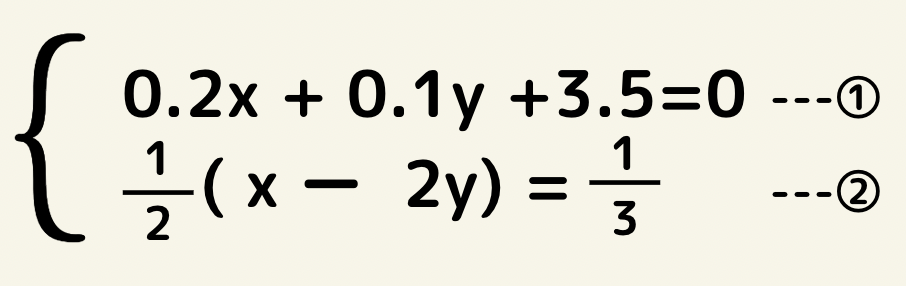
例えばこんな複雑な連立方程式でも余裕です^^
まずpoint1から 加減法で解こう!と方針を立てます。
次にpoint3から 係数を揃えたら良いことがわかります。
最後にpoint2から どんな操作をしたのか?記述をしていきます。

こうやってみると数字が複雑になっているだけで同じ解き方なのがわかりますね!
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#190



