京の算数学問題#022
アイデア数理塾はこちら
算数学コラム
方程式の本質をつかむ
中学に入ると方程式というものを学びます。
- x+3=4 とかのやつです。
この問題の場合は
- x = 4-3
- x =1
となるのですが
この①から②への変換のことを「移項」と言います。
正直慣れてくると方程式は簡単に解くことができますが、この単元で大切なのはいかに早くできるか?ではなく「移項ってそもそもなに?」が説明できるかどうかにあります。
この部分を説明できずして方程式は解くことができても理解することは出来ません。
今日はそんなお話。
そもそも方程式って何?
x+3=4
これが方程式なのですが、注目すべきは=(イコール)です。
=は等号とも言います。
読んで字の如く=を挟んで左と右の値は同じですよという意味です。
簡単にいえば、上記の式の場合
左辺 x+3と右辺4は等しいですよという意味になります。
つまり3に何を足したら4になるかを考えるわけです。
なのでx = 1になります。
ただ方程式も分数や項数が多くなってくるとこの解き方では限界があります。
そこでx=?という形に持っていくことで簡単に解くことができます。
つまり、一方にxのかたまりをつくりもう一方に数字のかたまりを作るということです。
これが「移項するということ」
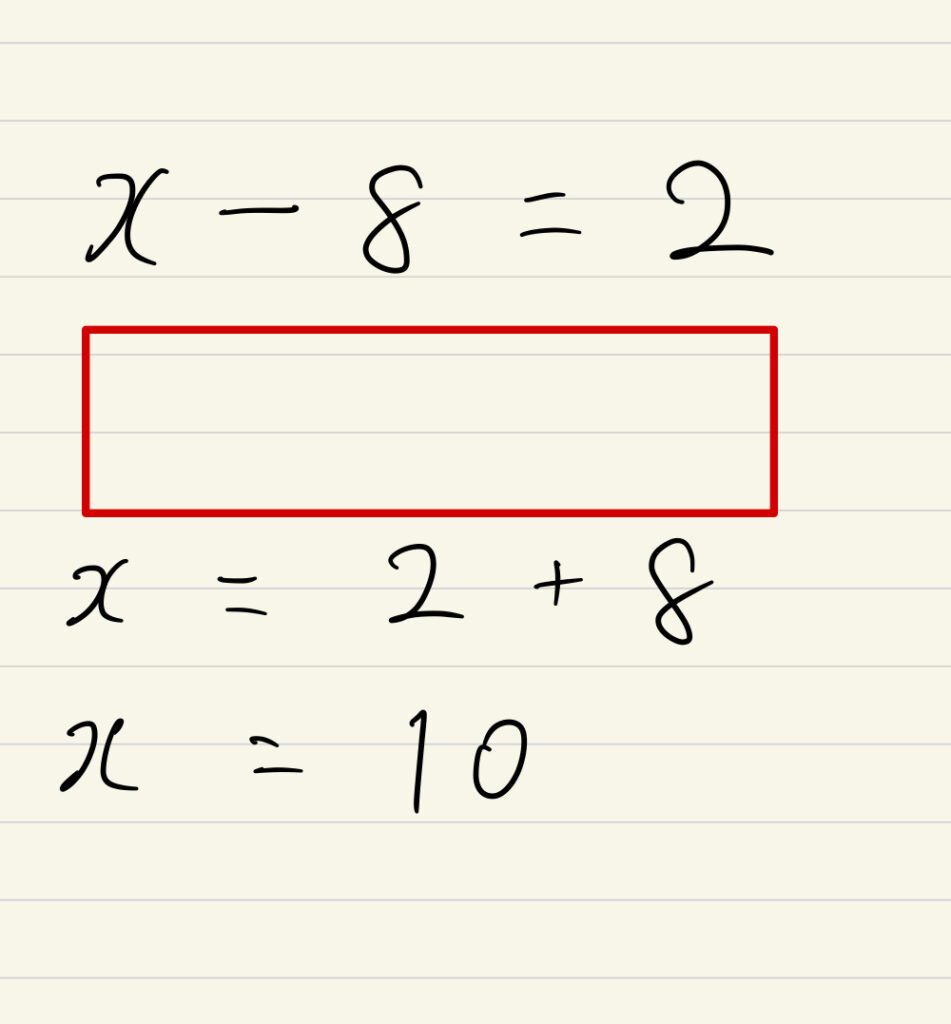
この時左辺の-8が右辺に+8と符号が変わって移動しました。
ただ、移項を理解するためには不十分です。
大切なのはこの赤の四角の部分のプロセスです。
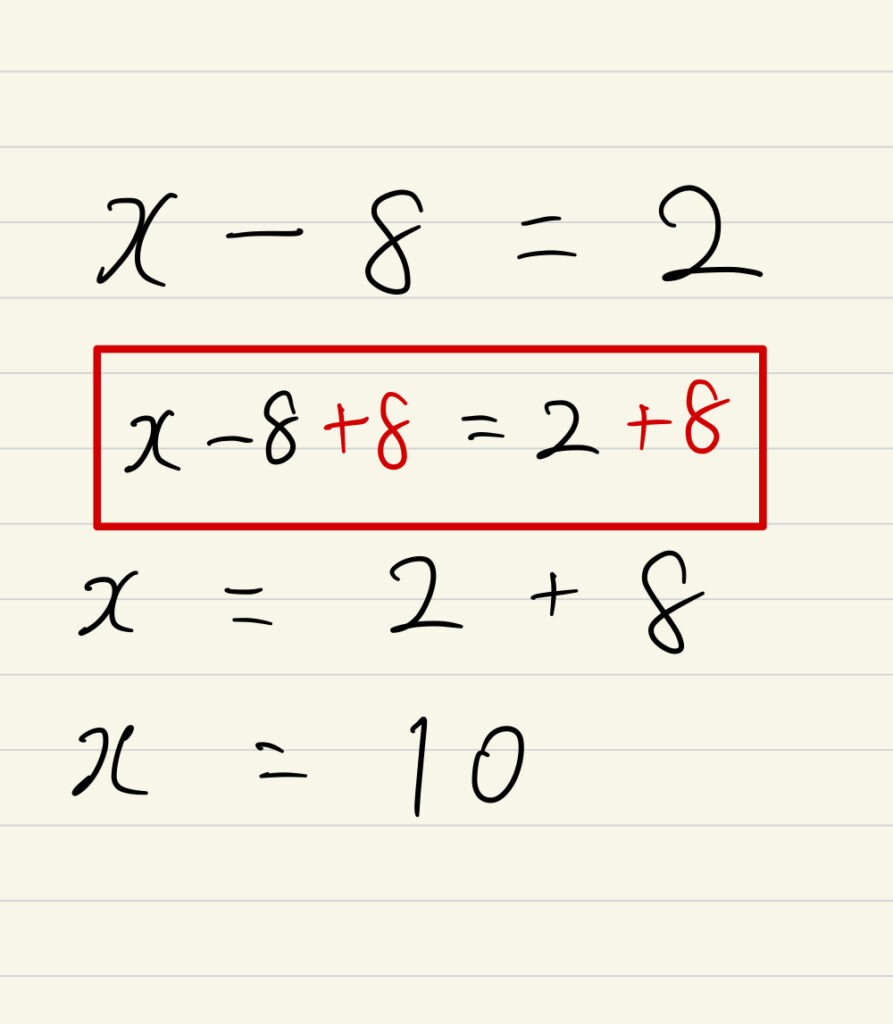
つまり左辺をx=にしたいので、―8が邪魔です。
―8に+8を加えると0になるのでxだけが残ります。
ですが=の左側に勝手に8を加えてしまったので、右側にも同様に+8をしないといけません。
そうすると左辺はxだけが残り右辺には2+8が残ります。
これが移項です。
符号を変えて移動したのではなく
=をはさんで、左右同じ操作をしたら項が移動したように“見える”だけなのです。
これをきちんと理解できれば応用が効きます。
例えば、文字式の問題では、
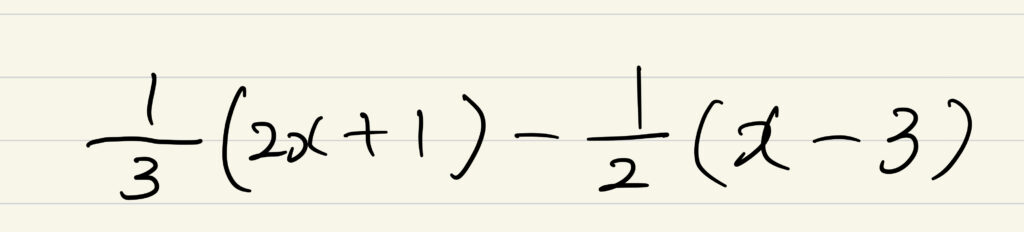
これを通常通りに解くと
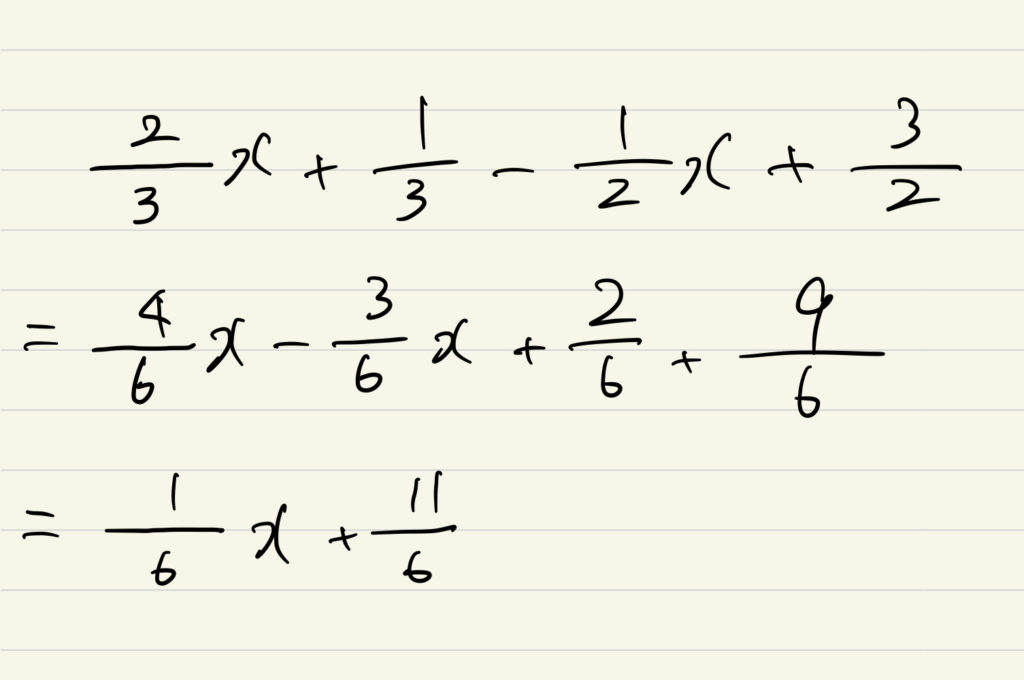
こうなります。
僕個人的にはこの解き方は見づらくミスが起きやすいと感じたので、

このように解いてみました。
文字式は方程式ではないので、かけっぱなしや割りっぱなしが出来ません。
計算を簡単にするためにまず分数を無くします。
全体に6をかけて計算をし、出た結果を6で割ると解答が出てきます。
この解き方も、きちんと理解ができているからこそできる解き方です。
中学時代の私は方程式を学んだタイミングでこれに気づき、お陰で大幅に正答率が上がりました。
もちろん「ミスをしやすくなる」と指摘された時もありますが、それはどんな解法でも言えることなので、数学の本質である実験を繰り返してみて、自分がやりやすい形にもっていくのが本来の勉強のやり方だと思います^^
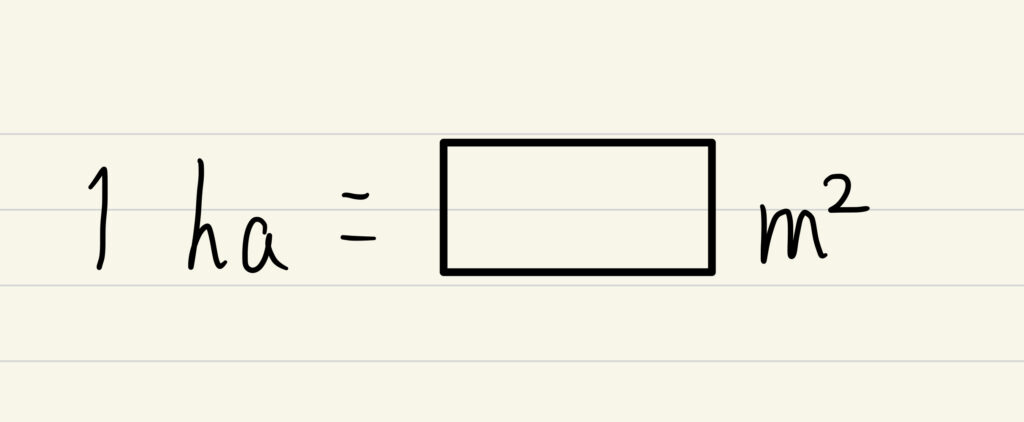
京の算数学 解答#022
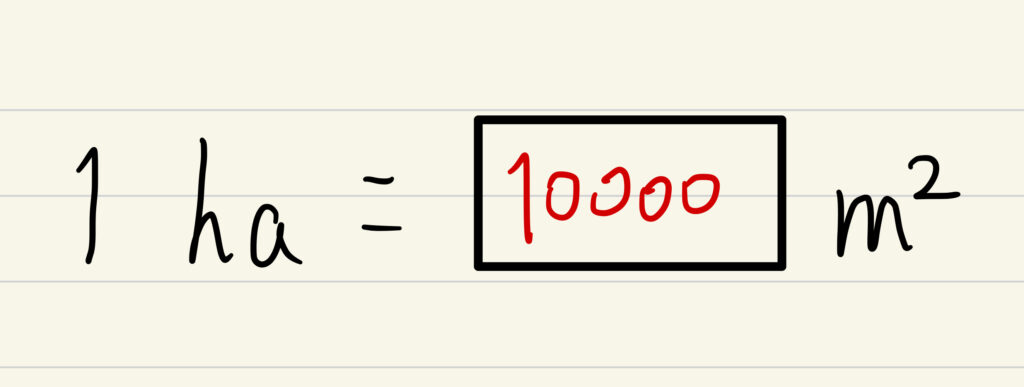
1ha(ヘクタール)=100a(アール)=10000m2(へいほうメートル)でした!



