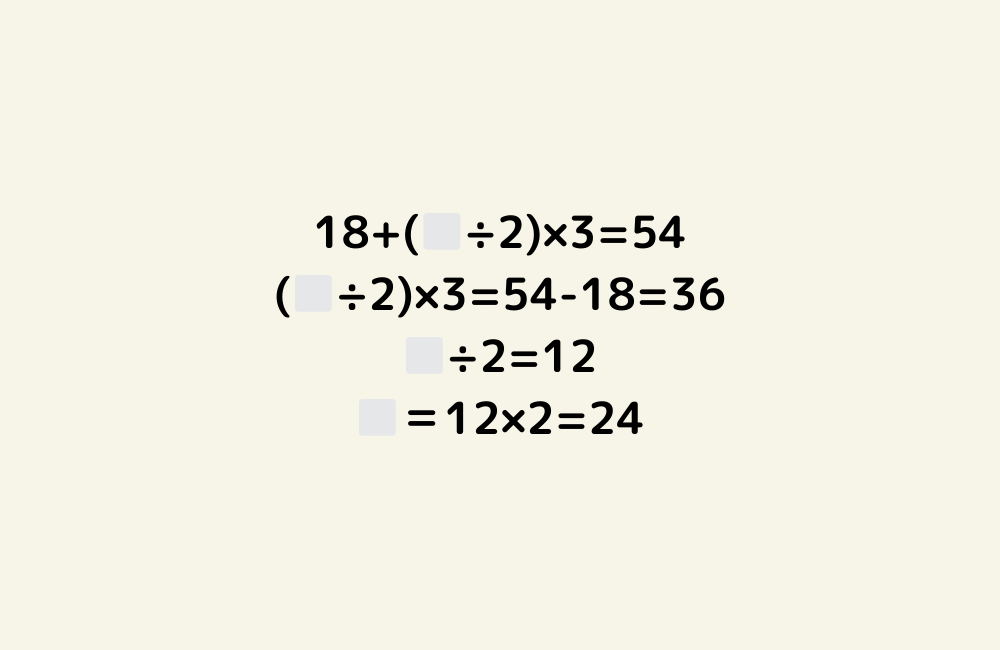数学コラムの目次
京の算数学問題#818

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
今日は「!」についてのお話をしていきたいと思います。
「!」とは「階乗(Factorial)」のことです。
4!=4×3×2×1といったように、1からその数までの全ての数を掛け合わせたものを表します。
ですが0!=1となるのです。
今日は階乗の不思議についてみていきます。
まずは具体例を見ていきましょう。
階乗の基本
たとえば、5!(5の階乗)を考えると次のようになります。
5! = 5 × 4 × 3 × 2 × 1 = 120
このように、5! は「5から1までの全ての数を掛けた結果」を示します。
これが階乗の基本的な考え方です。
それではもう少し簡単な例を見てみましょう。
4! = 4 × 3 × 2 × 1 = 24
さらに、大きな数も同じように計算できます。
10! = 10 × 9 × 8 × …… × 1 = 3,628,800
分数の階乗?
さて、少し応用問題です。分数の階乗も考えることができます。
(2/3)! = (2!) / (3!) = 2 / 6 = 1/3
このように、分数の階乗は単純に分子と分母の階乗を計算して、その比を求める形で表現できます。
0! 0の階乗は?
では、「0!」はどうなるのでしょうか?これは少し不思議な概念ですね。
計算の過程を見ていきましょう。
まず、階乗の定義から考えます。
n! = n × (n-1) × (n-2) × …… × 1
n-1! = (n-1) × (n-2) × …… × 1
このように、n! は n × (n-1)! と表されます。
では n=1 の場合を考えてみましょう。
1! = 1 × (1-1)!
1! = 1 × 0!
ここで、「1! = 1」であることが既にわかっています。
これを成り立たせるためには、0! = 1 としなければならないのです。
なぜ 0! = 1 と定義されるのか?
この「0! = 1」という結果は、実は「都合が良いから」定義されています。
数学的に便利なため、このように設定されています。
ここで重要なのは、「なぜ?」という問いに対して「都合が良いから」と答えることです。
通常、数学は定理や公式が「なぜそうなるのか?」を証明することで理解されます。
しかし、0! = 1 という定義は、「証明」ではなく「都合が良いからこうします」という解釈のもと成り立っています。
これは、高校数学で頻繁に出てくる考え方です。
数学の「強引さ」と「哲学」
このように、0! = 1 と定義することで、他の数式や計算がうまく成り立つようになります。
現実世界では経験できない事象も、数学ではこのように「都合が良いから」と定義して解決していくことが多々あります。
例えば、a² や a³ などの式は現実世界でも理解できますが、a⁰ など現実に存在しない数を扱うこともあります。
こういった「現実に存在しない概念」を使って計算を進めるのが、数学の「哲学的」な部分と言えるでしょう。
これが、数学が「現実を超えて推論する力」を持つ理由です。
時には強引な力技で進めていくことも必要であり、そうした考え方が数学が「哲学」とも言われる理由なのです。
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#818