数学コラムの目次
今日の数学問題#255

今日の数学コラム
解の公式は中学3年生で習う範囲なのですが初めて聞いた時に
「こんなの覚えられない!」
そうなりませんでしたか?
僕は実際なりました^^;
こんなの使わないじゃん!とも思いました。
ですが数学を教える立場になって気づいた事があります!
「解の公式はスゴイ」
今日は個人的に感じている解の公式の凄さについて語っていきます。
解の公式とは?
解の公式とはax^2+bx+c=0の時のxの解のことをいいます。
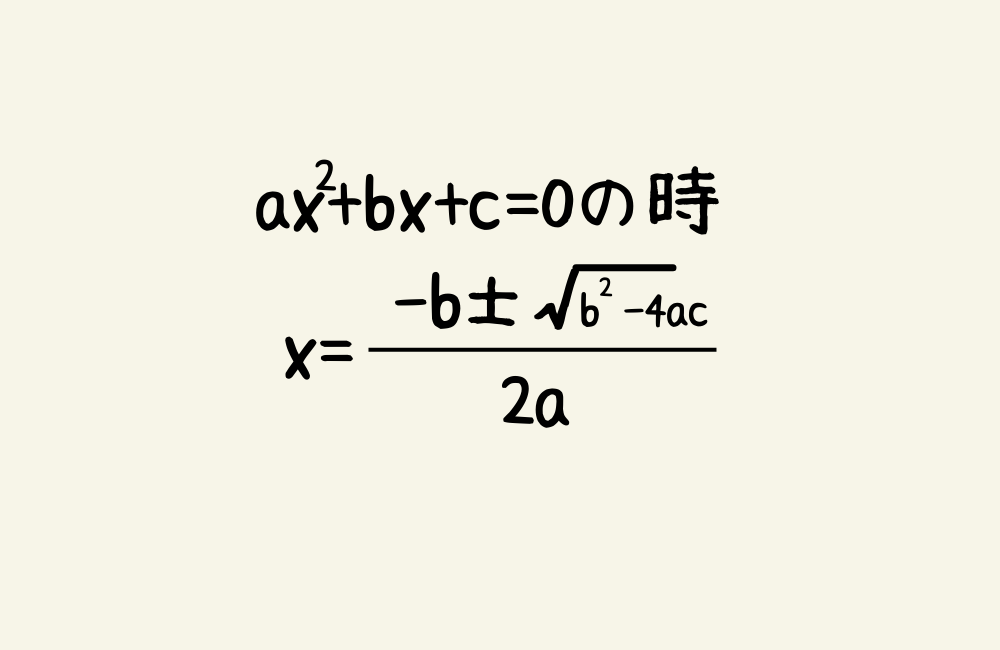
解の公式の証明
解の公式の証明はax^2+bx+c=0の式をxについて解くだけで求まります。
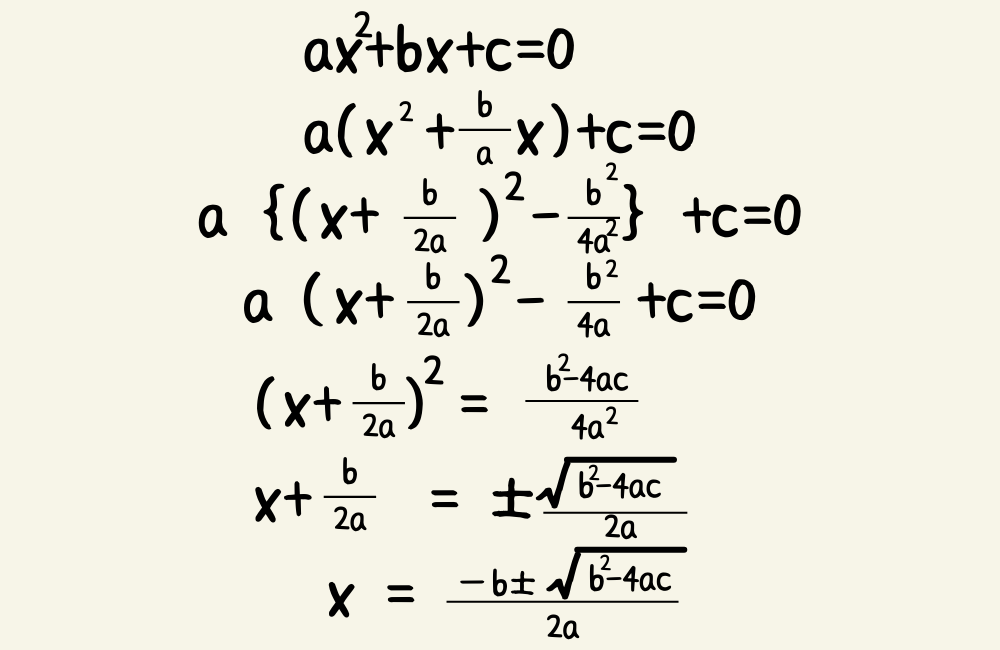
計算方法がややこしいですが基本的には平方完成さえできればなんとかなります。
たまに模試にもこの手の証明はでたりするのでしっかり押さえておきましょう!
解の公式の何がスゴイのか?
解の公式のルートの中b^2-4acを判別式と言います。
判別式は2次方程式においての解の個数を判別するためのものですが、なぜルートの中だけを見るのか?
生徒に聞いてもD>0のとき2個、D=0のとき1個、D<0のとき解はなしと答えられても実際になぜそうなるのか?と聞かれると固まってしまう事も多いです。
これはルートの中は基本的には正の実数であるという条件があるからです。
ルートの中が0より大きければ、当然±があるのですから2通り出てきます。
ですがルートが0であれば±も関係ないですよね。
ルートの中がマイナスならそもそも存在しないわけですから解はありません。
このようにルートの中を判別式とするという着眼点すばらしくないですか?
またこの公式にはax^2+bx+c=0のときという前提条件があります。
よく
2x^2+4x-3=3などの場合に
左辺に適用するミスをする生徒がいますが、この前提条件や成り立ちが必ず公式にはあるという事が素晴らしいのです。
解の公式から学ぶ日常での活用法
このことから転じて思うのは日常生活でもみんなが当たり前にしていることやものは、文化的な成り立ちや前提があるのでそれを度外視してはいけないよと言う事です。
数学は哲学なのでいろんな思考があります。
しっかりと身につけて生かしていきましょうね^^
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
今日の数学 解答#255



