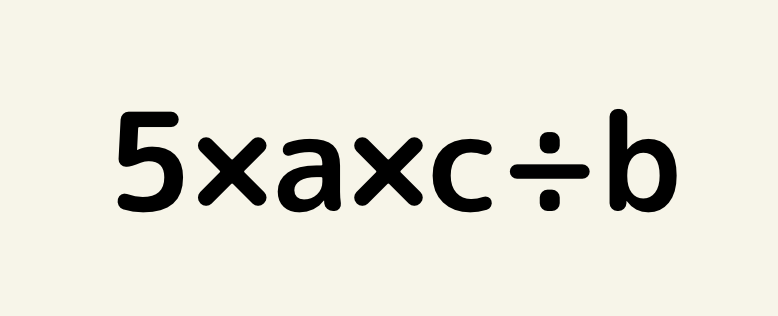アイデア数理塾 今日の数学問題#187
今日の数学コラム
連立方程式に少し慣れてくるととある疑問が出てきます。
「結局加減法だけでいいんじゃない？」
そう思ったそこのあなた！かなり損してます！
正直なところ加減法だけでも解くことは出来ます。
ですが、代入法も学ぶ事は必要とされています。それはなぜでしょうか？
連立方程式は加減法と代入法どちらも覚える必要があるのか？
結論あります！
学習指導要領では、基本的には不必要なものは無く連立方程式も多様な手段を用いて解くことによって視野を広げたり、さまざまなアプローチを自分で使えるようにする事が狙いの一つとしてあります。
なのでテストでも代入法で解けと指定をされてしまう場合があるのです。
加減法しか知らないと答えは合っているのに減点されてしまいますよね。
非常にもったいない！
また、次の単元に1次関数があるのですが、1次関数ではy=の形が多く出てくるので代入法で解くことが多くなります。
計算においても、使い分けが出来れば大きく時短ができます。
なので是非とも両方覚えておきたいところです。
連立方程式の解法見分け方
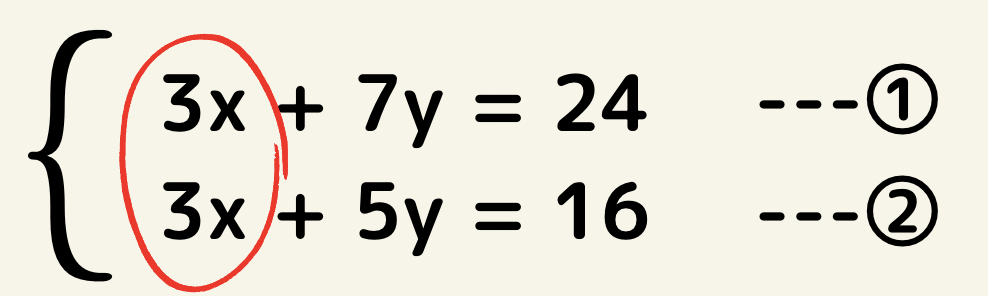
このように、共通の係数があった場合は迷わず加減法で良いです。
また、左辺に文字が偏っている場合に関しても基本的には加減法だと思っていいです。
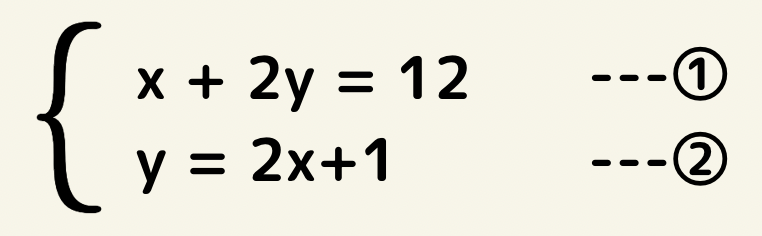
このようにy=、x=のような形の場合は代入法が良いです。
移項して加減法でも解けますがそのまま代入しちゃった方が早いです。
「式の形に注意をしてどちらを使うかを決める」のが基本です。
代入法が便利すぎる5分時短テクニック
例えば
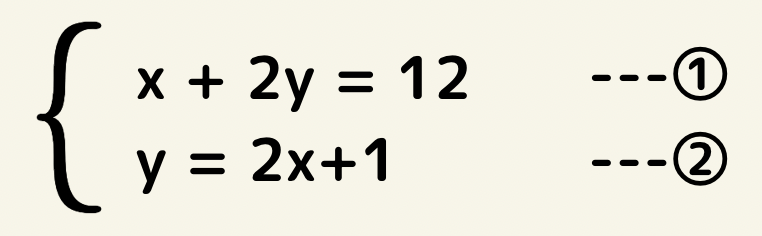
この場合②を①にそのまま代入すると、
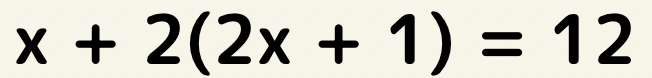
となり、分配法則をして解答します。
式が複雑になったりするとこの分配法則でミスをすることがあるために、
あらかじめ②×２をして代入します。
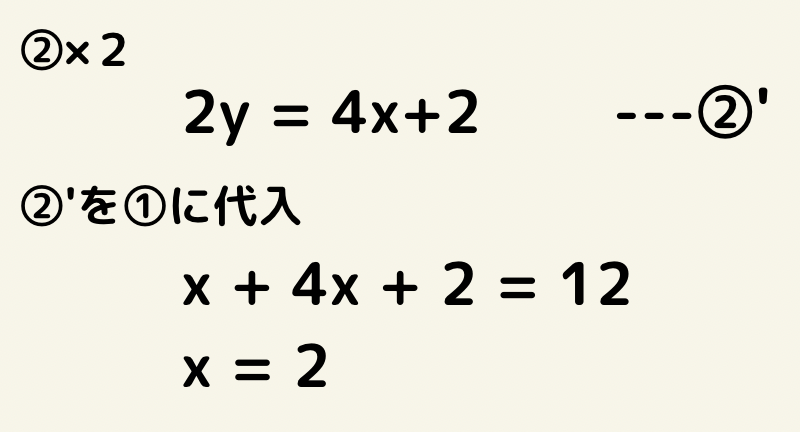
そうすると2yにそのまま代入ができるので比較的見やすい状態で計算をすることが出来ます。
このやり方を応用すれば、
加減法で解くよりも代入法で解く方がスムーズに解ける場合があります。
係数を揃えてから代入するというテクニックもぜひ覚えておいてください。
以上！京都市中京区のアイデア数理塾 油谷がお届けいたしました！
今日の数学 解答#187
