数学コラムの目次
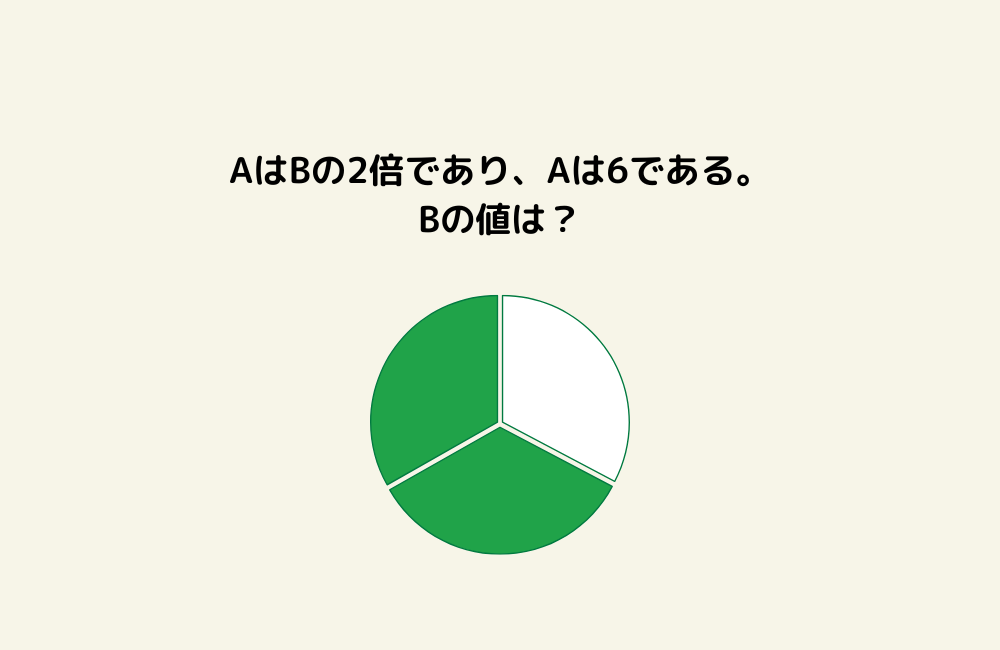
京の算数学問題#1264

アイデア数理塾はこちら
算数学コラム
数学の中でも、子どもにとってまず初めにぶちあたる壁がー×ーです。
「マイナス × マイナス = プラス
……って覚えなさい」
と言われるものの、ほとんどの子は、
- 「なんで???」
- 「覚えるしかないやん」
- 「ルールでしょ?」
とモヤモヤしたまま進みます。
でも本当は、ちゃんと理由があるんです。
今日は、塾でもよく使う
「超シンプルでイメージしやすい説明」だけを紹介します。
① “数直線”で考えると一番わかりやすい
まず、マイナスを「逆方向に進むこと」と考えてみます。
+(プラス)は“前に進む”
−(マイナス)は“後ろに進む”
というイメージを持ちましょう。
算数と数学の違いはここにあります。
プラスは大きい、マイナスは小さいと覚えてしまうとまずここでつまづきます。
あくまで一方向をプラスと仮定すると逆方向がマイナスを意味するという意味をまず理解しましょう!
「プラス × マイナス」
たとえば
3 × (-2) = -6
これは、
- 「-2 の方向に」
- 「3回進む」
つまり後ろ向き(マイナス方向)に3回進む=ー6
これはイメージしやすいですよね。
じゃあ「マイナス × マイナス」は?
ここで大事になるのが、
“前に進む” × “後ろに進む” ではなく、
“後ろ向きに進むことを、後ろ向きにする”
という考え方。
たとえば、
-1 × (-1)
これは、
「後ろに1歩進む」という動きを
“後ろ向き(逆方向)にする”
という意味になります。
「後ろ向きの動きを、さらに後ろ向きにひっくり返す」と前向き(プラス)になる。
だから、
-1 × (-1) = +1
となるわけです。
② “気持ちの向きをひっくり返す”イメージで考える
小学生にもめちゃくちゃウケる説明が
マイナスは「反対にする」スイッチ
- プラス × マイナス
→ 反対方向に進む - マイナス × マイナス
→ 反対方向に“反対をかける”からプラスになる
つまり…
マイナスは「ひっくり返しボタン」
ひっくり返しを2回すると元に戻る。
マイナス × マイナス = プラスは、「2回ひっくり返す」イメージで説明するだけで子どもは一気に納得します。
③ “借金”のたとえを使うと、感覚的に理解できる
もうひとつ簡単な例え。
「マイナス=借金」と考えます。
たとえば
「借金が−1万円」
これはわかりやすい。
じゃあ
「−1万円の借金が“−1回”になる」
とは何か?
借金を“マイナス1回する”=借金をなくす
借金を取り消す、なくす、帳消しにする。
つまり
+1万円の得になる
→ プラスになる
だから
-1 × (-1) = +1
になるわけです。
④ 子どもが一番つまずくのは「覚えるだけ」の状態
実は、
「マイナス×マイナス=プラス」を
“暗記で乗り切ろう”とする子ほど後でつまずきます。
理由は簡単で
- 文章題についていけない
- 方程式の符号ミスが増える
- 図形の移動・ベクトルで苦労する
- 理科(電流・仕事)でも混乱する
「理由を知っておく」だけでミスが激減します。
だから、今日紹介したような
- 数直線のイメージ
- ひっくり返しスイッチ
- 借金の逆転
のような“感覚的な説明”がとても大切なんです。
最後に
子どもたちは、納得できると一気に数学が理解できます。
「マイナス × マイナスはプラス」
こんな小さなことでも、
理解できた瞬間、
- 自信になる
- 数学への安心感が生まれる
- 次の単元へ前向きに進める
そんな“良い流れ”が始まります。
数学は暗記より、気持ちよく腑に落ちるかどうか。
これを大事にしていきたいですね。
京都市中京区・アイデア数理塾では
こうした“納得する数学”を大切にしています。
- 公式の意味
- なぜそうなるのか
- 図での理解
- 子どもが説明できるレベルの腑に落ち方
「覚える数学」ではなく
“わかる数学”を一緒に作っていきます。
京の算数学 解答#1264