数学コラムの目次
京の算数学問題#926

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で学習塾を運営しております、油谷拓哉(ゆたに たくや)です。
「分数の割り算ってなんでひっくり返すの?」
と聞かれたことはありませんか?あるいは、子どもに質問されて困った経験があるかもしれません。
「そういうものだから」と教えるのは簡単ですが、子どもたちの好奇心を刺激し、納得してもらうためにはもう少し丁寧に説明してあげることが大切です。
今回は、「分数の割り算がひっくり返る理由」をわかりやすく解説します。
保護者の方や先生方が子どもたちに説明する際の参考になれば幸いです!
分数がひっくり返る理由を理解する前に:割り算の基本をおさらい
分数の割り算を考える前に、まず割り算の性質を確認してみましょう。
割り算の基本的な性質
割り算には、次のような性質があります。
「割られる数と割る数に同じ数をかけても答えは変わらない」
たとえば、以下の例を見てみましょう。
- 18 ÷ 2 = 9
- 36 ÷ 4 = 9
- 54 ÷ 6 = 9
どれも同じ「9」が答えになっていますね。
割る数(2、4、6)に同じ数をかけても結果が変わらないのは、この性質のおかげです。
割り算を「1にする」という考え方
ここで、「割る数を1にしてしまう」と考えてみます。
たとえば、18 ÷ 2 を計算するとき、割る数の「2」に逆数(1/2)をかけて1にすることで、以下のように簡単に考えられます。
- 18 ÷ 2 = 18 × (1 ÷ 2) = 18 × 1/2
これが、分数の割り算で「ひっくり返る」基本的な考え方につながります。
分数の割り算で「ひっくり返る理由」を式で説明!
では、実際に分数の割り算がなぜひっくり返るのかを具体的な例で見てみましょう。
例:1/2 ÷ 1/4 の場合
1/2 を 1/4 で割る計算を考えます。
この割り算をかけ算に直すと、次のようになります。
1/2 ÷ 1/4
= 1/2 × 4/1
= 4/2
= 2
ここで、割り算をかけ算に直すときに「割る数をひっくり返す(逆数をとる)」 という操作が行われています。
なぜこれが成り立つのでしょうか?
割り算をかけ算に変える理由
割り算は、かけ算の逆の操作です。
たとえば、18 ÷ 2 = 9 をかけ算に直すと、2 × 9 = 18 という関係が成り立ちます。
分数の場合も同じです。
1/2 ÷ 1/4 をかけ算に直すと、「何をかければ元の数になるか」を考えることになります。
その答えが 「逆数をかける」 という操作なのです。
イメージで理解しよう!分数の割り算の具体例
数字や式だけではイメージがつかみにくい子どもたちには、具体的な状況を例に出すのが効果的です。
例:ピザを使って考える
1枚 のピザを、1/4 の大きさずつ分けたら何枚になるでしょうか?
1 ÷ 1/4 を計算すると、
- ピザの1を「1/4の大きさ」に分けると、ちょうど4枚になることがわかります。
これを図や絵を使って説明することで、子どもたちは直感的に理解しやすくなります。
ガソリンの例で考える:単位量の理解
もう一つの例として、「単位量」を使った説明も有効です。
ガソリンと走行距離の例
40リットルのガソリンで400km走る車があるとします。
ガソリン1リットルで何km走れるかを計算する場合、次のように考えます。
400 ÷ 40 = 10(1リットルあたり10km)
これを分数に置き換えると、400 ÷ 1/40 = 400 × 40/1 となり、「割り算がかけ算に変わる」理由がイメージしやすくなります。
図形でわかりやすく!分数の割り算を視覚化しよう
最後に、図形を使った説明も取り入れてみましょう。
たとえば、1 ÷ 1/4 を考える場合、次のように説明します。
- まず、1枚のピザを作ります。
- 次に4等分することで、1/4のサイズがいくつあるかを確認します。
- 結果として、「4つある」という答えが視覚的にわかります。
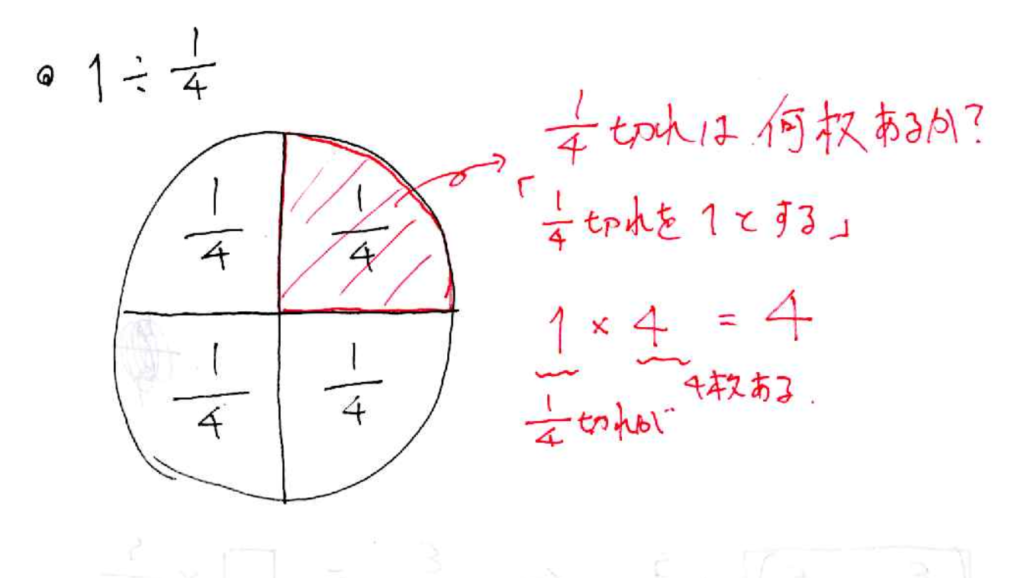
まとめ:分数の割り算は「逆数をかける」で簡単に解ける!
分数の割り算がひっくり返る理由を、式、具体例、イメージを使って説明してきました。
大切なのは、子どもたちに「そういうもの」と丸暗記させるのではなく、 「なぜそうなるのか」 を丁寧に伝えて納得してもらうことです。
分数の世界は少し難しいですが、興味を持って学べるように工夫して教えると、子どもたちの算数力がぐっと伸びます!
以上!京都市中京区のアイデア数理塾、油谷拓哉(ゆたに たくや)がお届けしました!
算数好きあつまれ〜!
京の算数学 解答#926




