数学コラムの目次
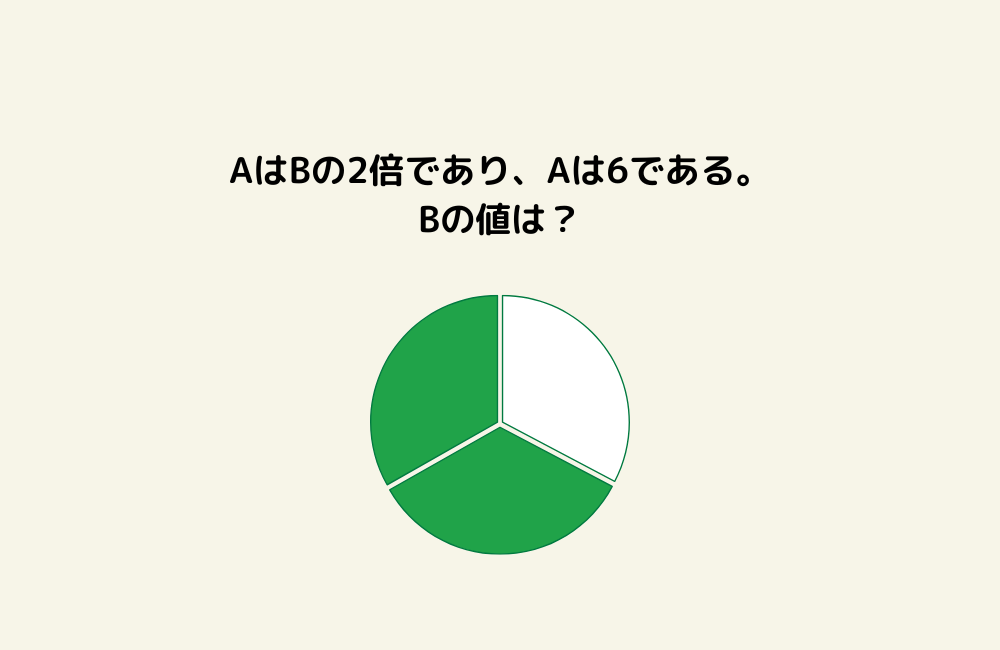
京の算数学問題#1266

アイデア数理塾はこちら
算数学コラム
中学に入ると、急に出てくる“代数”という言葉。
- 「文字を使うやつ?」
- 「xとかyが出てくるあれ?」
- 「数字のほうが簡単だったのに…」
多くの子が、
“算数 → 数学”の大きな壁をここで感じます。
でも本当は、代数って難しいものではなく、
「数字だけでは説明できないことを、文字で自由に扱えるようにした考え方」なんです。
つまり、“自由に考えるための数学の道具” が代数。
今日は、数学が苦手な子でもわかるように解説していきます。
まず、代数は「文字で考える数学」
算数までは、基本的に数字しか出てきません。
- 3+5
- 12÷4
- 6×8
すべて“決まった数字”が出てきます。
でも、数学になると一気に自由度が上がり、
「数字が何かわからない状態」
を扱えるようになります。
例えば
- x+5
- 2y-3
- 3(a+b)
「数字を文字で表す」これが代数のスタートです。
代数って何に使うの?
「なんでわざわざ文字を使うの?」
子どもからよく聞かれる質問です。
理由は3つあります
①まだ決まっていない数字を扱える
たとえば、
「ある数に5を足すと12になる」
これを算数だけで考えると、
文章から1つずつ推理していく必要があります。
でも代数なら
x + 5 = 12
たったこれだけ。
あとは計算すればOK。
②:どんな数字にも当てはまる共通ルールを作れる
(a+b)²=a²+2ab+b²
これは“aとbが何であっても成り立つ”式です。
つまり
「特定の数字だけ」ではなく「すべての数字に共通する法則」
を表せるのが代数。
代数は、言い方を変えれば公式を自ら作ることのできるツールだと言えます。
③:図形・関数・確率など、他分野につながる
代数は数学の基礎。
ここができると
- 方程式
- 連立方程式
- 関数
- 図形の証明
- 確率
- 速さ・割合
など、数学のあらゆる分野が一気に理解しやすくなります。
つまり代数は“数学の文法”のようなもの。
代数を“子どもにわかりやすく説明すると”…
「代数は、“箱”の中に何が入っているかは決まっていないけど、とりあえず計算できるようにした考え方」
xという箱があり、その中身はまだ分からない。
- x+3
- 2x
- x-7
こうやって式にしておけば、後から中身が決まっても使える。
方程式をまだ学んでいない小学生でも納得した例は、
「箱に5を入れると10になる。じゃあ箱には何が入っている?」
式にすると
x + 5 = 10
だから x=5。
「箱」だとイメージしやすいんです。
代数が苦手になる子の共通点
代数がわからなくなる子には、3つの共通点があります
① 文字を“記号”としてしか見ていない
xは“数字の入る場所”なのに、“よくわからない記号”と思ってしまう。
② 計算の順番・ルールが曖昧
カッコ、符号、分配法則など、
代数の基本ルールが曖昧なまま進むと一気に崩れます。
③ 文章題で“何をxにするか”決められない
ここで苦手になる子が非常に多いです。
基本的には文章で問われている数をxとおきます。
初めは作業的でもいいので〇〇をxとするという一文を入れる癖をつけましょう!
代数を得意にするためのコツ
代数という分野は、
実は“センス”よりも“慣れ”がすべてです。
コツ①:文字を「数字の入れ物」として扱う
xやaは“入れ物”。
入れ物だと思えば、計算が自由にできる。
コツ②:分配法則・符号の扱いを“徹底して”練習
難しい計算は必要ありません。
- 符号
- カッコ
- -をかけたときの変化
- 同類項をまとめる
これができると、代数は一気に楽になります。
コツ③:文章を「自分の言葉で」式に変える練習
文章 → 自分の言葉 → 式の順で変換すると、子どもでもつまずきにくい。
最後に
代数は、
“数学が急にムズく感じる入口”と言われる単元ですが、
本当はとてもシンプルな考え方です。
- まだ決まっていない数字を扱える
- どんな数字でも成り立つルールを作れる
- 数学全体の土台になる
代数を理解するということは、
「数字の世界から、考える世界へ」扉が開く
ということなんです。
子どもが代数を理解した瞬間、
数学に対する不安がスッと消えていくのを、
何度も見てきました。
焦らず、少しずつ。
代数は、ゆっくり慣れれば必ずわかります。
京都市中京区・アイデア数理塾では
代数が苦手な子に向けて、
- xをどう扱うかの基礎
- 計算のルール整理
- 文章題を式にする練習
- 図で考える代数
- 「わかった」を「説明できる」に変える授業
を大切にしています。
代数に入ってつまずいた…というお悩みがあれば、いつでもご相談ください。
京の算数学 解答#1266