数学コラムの目次
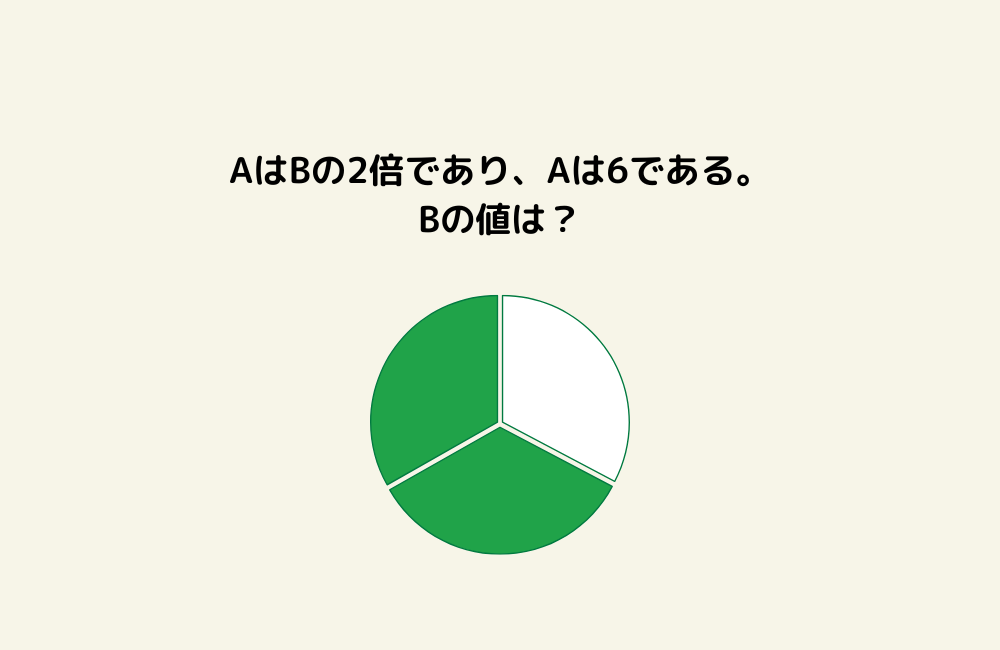
京の算数学問題#997

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で学習塾を運営しております、油谷拓哉(ゆたに たくや)です。
「前は解けていたのに、久しぶりにやったらできなくなってしまった…」
「うちの子、前に教えたはずなのに忘れてしまっている…」
こうした相談を保護者の方から受けることは本当に多いです。
でも、算数の解き方を忘れてしまうのは小学生では当たり前のこと。
むしろ、それを前提にして指導を組み立てていくことが大切です。
今日は、なぜ算数の解き方を忘れてしまうのか、そしてどうすれば忘れにくくなるのかについて考えていきます。
なぜ算数の解き方を忘れてしまうのか?
算数の解き方を忘れてしまう理由は、「理解」ではなく「暗記」に頼っているからです。
ただ覚えるだけでは忘れやすい
たとえば、
三角形の面積 = 底辺 × 高さ ÷ 2
この式自体を覚えている子は多いですが、なぜ÷2なのかを理解している子は意外と少ないです。
▶︎ なぜ÷2なのか?
- 三角形を2つ組み合わせると平行四辺形ができる
- 平行四辺形の面積 = 底辺 × 高さ
- だから三角形はその半分 → ÷2
「式」ではなく「成り立ち」を理解しているかどうかがポイントです。
理解が浅いままだと応用が効かない
単なる暗記だけだと、
- 少しでも問題の形が変わると解けなくなる
- 似た問題なのに応用が効かなくなる
公式や解き方の「理由」まで理解していると、形が変わっても応用が可能になります。
人は忘れる生き物
忘れてしまうのは自然なことです。
ドイツの心理学者ヘルマン・エビングハウスが提唱した「忘却曲線」という理論があります。
忘却曲線とは?
- 暗記した内容は1時間後に約50%を忘れる
- 1日後には約70%、
- 1週間後には約80%を忘れる
つまり、何もしなければ1週間後にはほとんど忘れてしまうのです。
記憶の定着に必要なのは「思い出すこと」
「忘れる」は自然なことですが、復習を繰り返して思い出すことで記憶は強化されます。
- 学んだことを何度も繰り返す
- 思い出す作業を取り入れる
これにより、記憶が「短期記憶」から「長期記憶」へと移行していきます。
小学校のカリキュラムは「思い出す」工夫がされている
実は、小学校のカリキュラムには「忘却曲線」を考慮した仕組みが取り入れられています。
カリキュラムの特徴
- 毎年同じ単元を繰り返し学ぶ
- 低学年で学んだ内容が高学年で再登場する
- 復習が組み込まれている
▶︎ これは「思い出す」プロセスを通じて、記憶を定着させるための仕組みです。
算数の解き方を忘れないようにする方法
では、具体的にどのようにすれば算数の解き方を忘れにくくなるのでしょうか?
以下の方法を実践してみましょう。
① 公式を「理解」する
公式や解き方の理由を理解することが大切です。
例:円周の公式
円周 = 直径 × 3.14
ここで「なぜ×3.14なのか?」を説明します。
- 直径を「円の幅」と考える
- 円を平たく広げると、その長さは直径の約3.14倍になる
▶︎ こうした成り立ちを理解すると、応用問題にも対応しやすくなります。
② 「完璧に教え込まない」
すべてを最初から完璧に教え込むのではなく、
- ある程度のヒントを与える
- 自分で考えるプロセスを作る
▶︎ 考える余地を与えることで、記憶に残りやすくなります。
③ 「わかった気になる」を防ぐ
答えを見て理解しただけで終わらせないことが重要です。
- 答えを見て理解した後、
- 何も見ずにもう一度解く
- できなければもう一度確認
この繰り返しが記憶の定着につながります。
④ 思い出す作業を増やす
「思い出す」ことで記憶は強化されます。
- 解いた問題を1日後、3日後にもう一度解く
- 少し間隔を空けてから再挑戦
これにより記憶が長期的に定着します。
⑤ 「間違い」を活かす
間違えることは悪いことではありません。
- 間違えた問題は記憶に残りやすい
- 間違いを訂正しながら理解を深める
間違いを恐れずに挑戦する姿勢を大切にしましょう。
まとめ
算数の解き方を忘れてしまうのは「暗記頼り」になっているから
「理解」による記憶は忘れにくい
人は忘れる生き物 → 「思い出す」ことで記憶を強化できる
小学校のカリキュラムは「復習」→「思い出す」設計
公式や解き方の「理由」を理解すると忘れにくい
「理解」+「思い出す」 を繰り返すことで、算数の力は着実に身についていきます。
焦らず、じっくり取り組んでいきましょう!
以上、京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けしました!
算数好きあつまれ〜!
京の算数学 解答#997