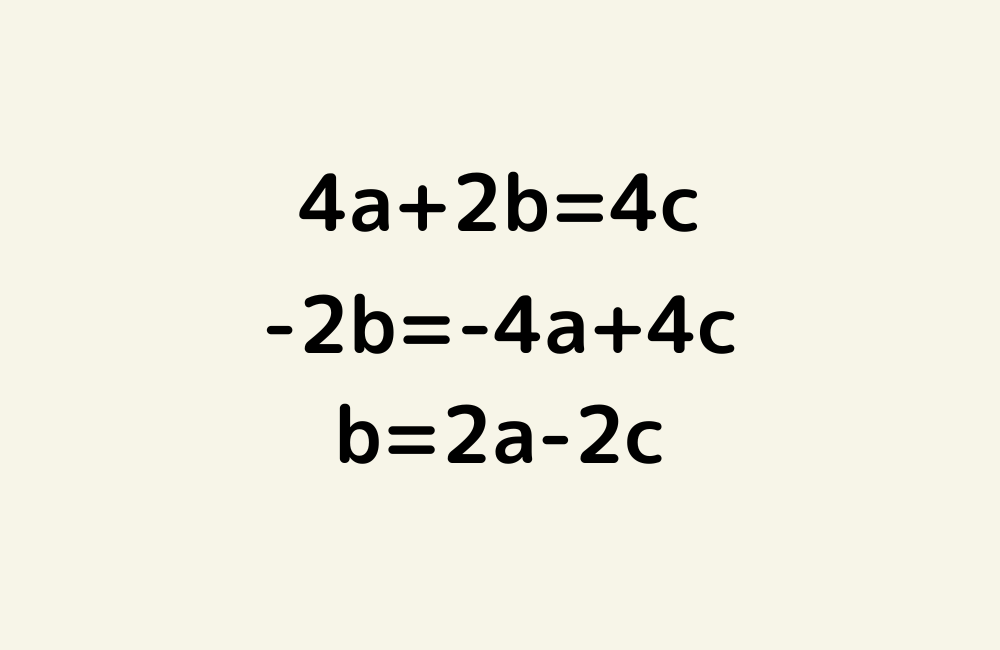数学コラムの目次
京の算数学問題#669

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
「うちの子、図形は得意なんですけどね、、、」
「方程式からつまづいていて、、、」
算数から数学になりより難しく感じる生徒さんも多いと思います。
今日は代数を得意になるためにどうしたらいいか?という問題の考え方についてお話ししていこうと思います。
代数ってなに??
代数とは、中学数学でいう文字式や一次関数など、数字の代わりに文字を使って計算や解法を考える分野のことです。
図形分野のことは幾何と言います。
代数は中学数学最初の関門であり入試では頻出の分野ですので代数で合否が決まるといっても過言ではないぐらいに重要な分野です。
代数が苦手な理由
代数が苦手な理由は以下が考えられます。
小学生の小数、分数の計算が理解できていない
小学生の単元である小数や分数の計算ができていないと文字式で表した時どの部分を割っているのか?また、小数を分数に直したりなど、計算においてなんの操作をしているのか?がわからなくなります。
単位量あたりが理解できていない
中学数学の代数ではその文字が何を表しているのか?を理解する事が大事です。
小学生で学ぶ単位量あたりは〇〇を1とするとという数字の扱い方や表し方を学ぶにはうってつけの範囲ですが、残念ながら代数が苦手だなあ、と感じる生徒はほとんどの場合単位量あたりが苦手です。
数字と文字の違いがわからない
代数は文字という抽象概念を使って数字を表しています。
例えばy=2xというのは比例の式なのですが、x=1の時y=2、x=2の時y=4とxとyどちらか片方が決まればもう一方の値がわかるという意味があります。
つまり小学生の時で言う◻︎や△を使った式と同じなのです。
ルールを複雑に覚えてしまっている
文字式のルールは、実は4つしかありません。
1の掛け算は省略すること(1a=a,-1c=-c)
×の記号と÷の記号は省略すること(2×a=2a,x÷3=x/3)
同じ文字同士は足し引きできる(a+3a=4a,6c-5c=c)
同じ文字の掛け算は指数で表す(a×a×a=a3)
この4つのルールさえ覚えておけば後は解く事ができるのですが、教科書にはさまざまな表現で同じ意味のルールが書かれているため全て丸暗記をしようとして理解できずに進んでいる場合が多いです。
代数を得意になるには?
まずは文字式になれる必要があります。
つまり4つのルールを理解し、きちんと計算ができると言うところから始めましょう。
次に文字式と方程式の違いなど特に代数は幾何のように具体物はなく表現が抽象的なので、言葉の意味をきちんと理解しておきましょう。
また、1つ1つの操作を「なぜそれをやっているのか?」という視点で考えることも大切です。移項とはなぜ符号が逆になるのか?関数はなぜ座標があるのか?代数分野は特に全ての学びの繋がりを意識しないと暗記だけで何とかすることになります。
文字式の利用が大切
代数を得意になるためには文章を文字式で表すと言う練習が最も効果的です!
例えば一辺がacmの正方形の周りの長さは4acmです。
この4aとはaが4本あると言う意味なのですが、文章をたった1つの式で表す事ができると言うのが代数のおもしろさです。
もしも代数を得意になりたい!と思ったらまずは文字式のルールをマスターし、そのあとで文字式の利用に取り組んでみましょう!
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#669